Теорема Пифагора

Пифагор Самосский (ок. 580 - ок. 500 до н. э.) древнегреческий математик и философ-идеалист.

Геометрическая формулировка.
Изначально теорема была сформулирована следующим образом:
Алгебраическая формулировка.
То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b:
a2 + b2 = c2
Обратная Теорема Пифагора

Доказательства
1) Через подобные треугольники
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения
получаем
Что эквивалентно
Сложив, получаем
или

2) Доказательство методом площадей
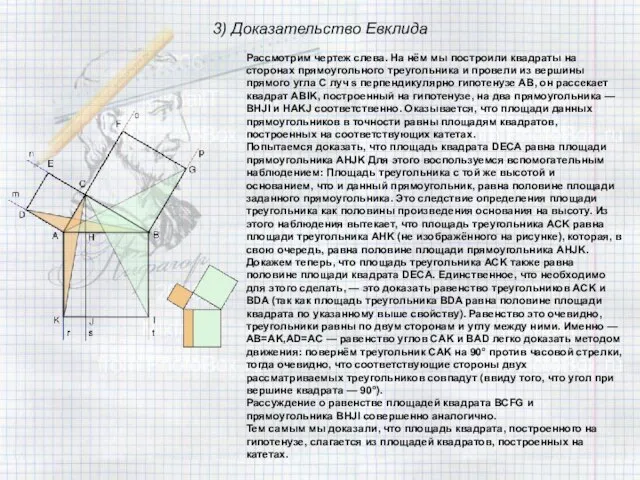
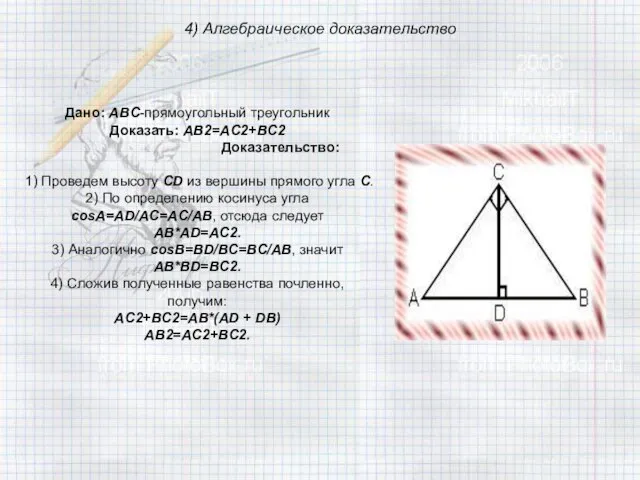
Дано: Прямоугольный треугольник с катетами а и b и гипотенузой с.
Доказательство:
Достроим этот треугольник до квадрата со стороной a+b .
У этого квадрата сторона а+b , а его площадь равна S кв = (a+b)2
С другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников и четырёхугольника со стороной с, который является квадратом, т.к.<1=<3=<5=<7 и <2=<4=<6=<8 => <1+<8 = <2+<5 = <3+<6 = <4+<7 =900.
Найдём площадь квадрата: S кв =4Sтр + с2 =4·1/2 ab + c2 = =2ab + c2. Тогда (a+b)2 = 2ab+c2,
a2 + 2ab + b2 = 2ab +c2 , a2 + b2 = c2.
1 8
7
6
4 5

3) Доказательство Евклида
Рассмотрим чертеж слева. На нём мы построили квадраты на сторонах прямоугольного треугольника и провели из вершины прямого угла С луч s перпендикулярно гипотенузе AB, он рассекает квадрат ABIK, построенный на гипотенузе, на два прямоугольника — BHJI и HAKJ соответственно. Оказывается, что площади данных прямоугольников в точности равны площадям квадратов, построенных на соответствующих катетах.
Попытаемся доказать, что площадь квадрата DECA равна площади прямоугольника AHJK Для этого воспользуемся вспомогательным наблюдением: Площадь треугольника с той же высотой и основанием, что и данный прямоугольник, равна половине площади заданного прямоугольника. Это следствие определения площади треугольника как половины произведения основания на высоту. Из этого наблюдения вытекает, что площадь треугольника ACK равна площади треугольника AHK (не изображённого на рисунке), которая, в свою очередь, равна половине площади прямоугольника AHJK.
Докажем теперь, что площадь треугольника ACK также равна половине площади квадрата DECA. Единственное, что необходимо для этого сделать, — это доказать равенство треугольников ACK и BDA (так как площадь треугольника BDA равна половине площади квадрата по указанному выше свойству). Равенство это очевидно, треугольники равны по двум сторонам и углу между ними. Именно — AB=AK,AD=AC — равенство углов CAK и BAD легко доказать методом движения: повернём треугольник CAK на 90° против часовой стрелки, тогда очевидно, что соответствующие стороны двух рассматриваемых треугольников совпадут (ввиду того, что угол при вершине квадрата — 90°).
Рассуждение о равенстве площадей квадрата BCFG и прямоугольника BHJI совершенно аналогично.
Тем самым мы доказали, что площадь квадрата, построенного на гипотенузе, слагается из площадей квадратов, построенных на катетах.

4) Алгебраическое доказательство
Дано: ABC-прямоугольный треугольник
Доказать: AB2=AC2+BC2
Доказательство:
1) Проведем высоту CD из вершины прямого угла С.
2) По определению косинуса угла соsА=AD/AC=AC/AB, отсюда следует
AB*AD=AC2.
3) Аналогично соsВ=BD/BC=BC/AB, значит
AB*BD=BC2.
4) Сложив полученные равенства почленно, получим:
AC2+BC2=АВ*(AD + DB)
AB2=AC2+BC2.

5) Древнекитайское доказательство
В IX книге "Математики"- главном из сохранившихся математико-астрономических сочинений Древнего Китая- помещен чертеж (рис. а), доказывающий теорему Пифагора. Четыре равных прямоугольных треугольника с катетами a, b и гипотенузой c уложены так, что их внешний контур образует квадрат со стороной a+b внутренний - квадрат со стороной c, построенный на гипотенузе (рис. б). Если квадрат со стороной с вырезать и оставшиеся 4 затушеванных треугольника уложить в два прямоугольника (рис. с), то ясно, что образовавшиеся пустота, с одной стороны, равна с², а с другой - a²+b², т.е. с²=a²+b². Теорема доказана.