Теорема Пифагора

Пифагор Самосский
Древнегреческий философ и математик, великий ученый Пифагор родился около 570 г. до н.э. на острове Самос. По легенде, рождение ребенка будто бы предсказала Пифия в Дельфах, которая также сказала, что ребенок принесет столько пользы и добра людям, сколько не приносил и не принесет им никто другой. Отец Пифагора — Мнесарх — дал ребенку имя, которое означает «тот, о ком объявила Пифия».
Пифагор Самосский
570 - 500 гг. до н.э.

Древний Китай. Здесь особое внимание привлекает математическая книга Чу-пей в которой так говориться о пифагоровом треугольнике со сторонами 3, 4 и 5:"Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4".
История открытия теоремы

Известный немецкий математик, основоположник теории множеств, Георг Кантор считал, что равенство 32 + 42 = 52
было известно уже египтянам еще около 2300 г. до н. э.
По мнению Кантора гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
История открытия теоремы
Георг Кантор
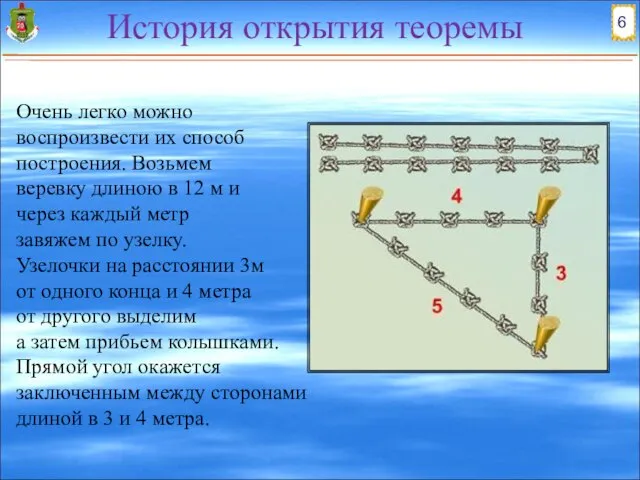
1845 – 1918

История открытия теоремы
а затем прибьем колышками. Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра.
Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12 м и через каждый метр завяжем по узелку. Узелочки на расстоянии 3м от одного конца и 4 метра от другого выделим

В Древнем Вавилоне были известны частные случаи теоремы Пифагора.
История открытия теоремы
Было известно, что если длины сторон прямоугольного треугольника выражаются в рациональных числах, то квадрат длины гипотенузы равен сумме
квадратов длин катетов. Знали уже и обратную теорему.

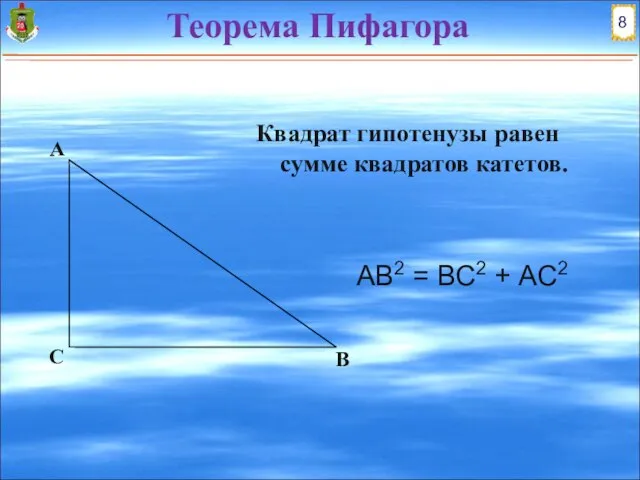
Теорема Пифагора
АВ2 = ВС2 + АС2
Квадрат гипотенузы равен сумме квадратов катетов.
А
В
С

Доказательство теоремы Пифагора
Дано: т-к АВС – прямоугольный, C – прямой угол, b1 – проекция катета b на гипотенузу, a1 – проекция катета a на гипотенузу, h – высота треугольника, проведенная к гипотенузе.
Доказать:
с

Доказательство:
1. Треугольники АВС и АСМ подобны по первому признаку подобия треугольников.
2. Из подобия этих треугольников следует, что b = cb1, a = ca1. Складывая почленно эти равенства получим a + b = cb1+ca1= c(b1+a1) = =c , ч.т.д.
А
В
С
b1
a1
h
М
с
a
b
Обратная теорема

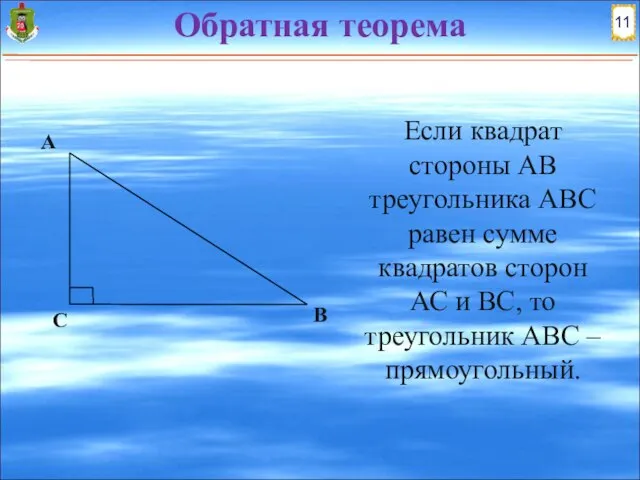
Если квадрат стороны АВ треугольника АВС равен сумме квадратов сторон АС и ВС, то треугольник АВС – прямоугольный.
Обратная теорема

Обратная теорема

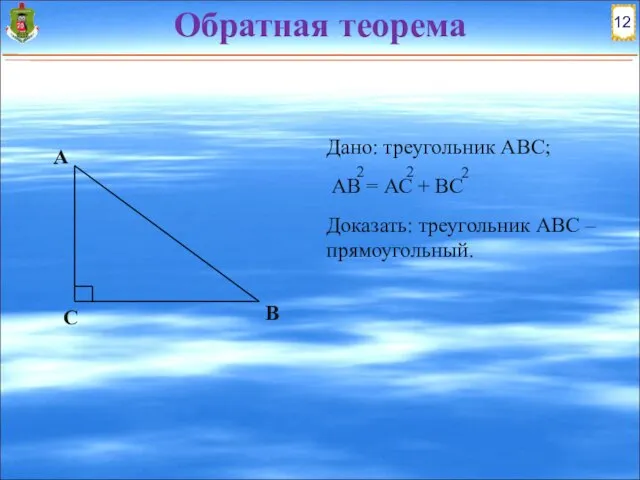
Доказательство обратной теоремы
Доказательство:
1.Дополнительное построение: т-к А1В1С1(А1С1 = АС, В1С1 = ВС, А1В1 = с, угол С1 – прямой). Т. к. т-к А1В1С1 – прямоугольный, то по теореме Пифагора имеем: с = ВС + АС
2.Сравниваем соотношения
и с = ВС + АС , получаем, что с = АВ или с = АВ.
3.Т-ки АВС и А1В1С1 равны по третьему признаку равенства треугольников. Из этого следует, что угол С равен углу С1, а значит т-к АВС– прямоугольный, ч.т.д.
АВ = АС + ВС