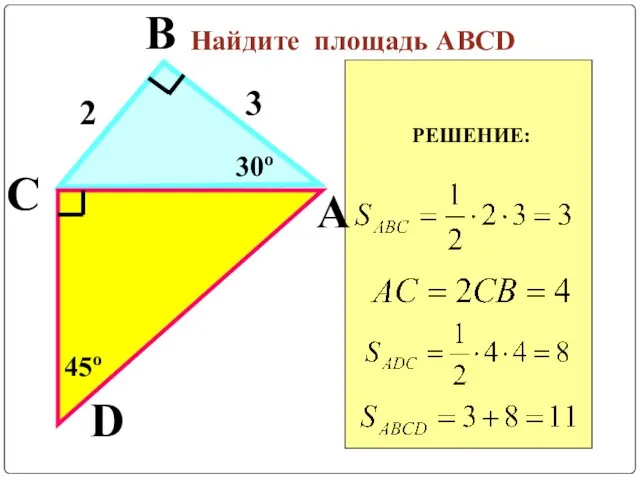
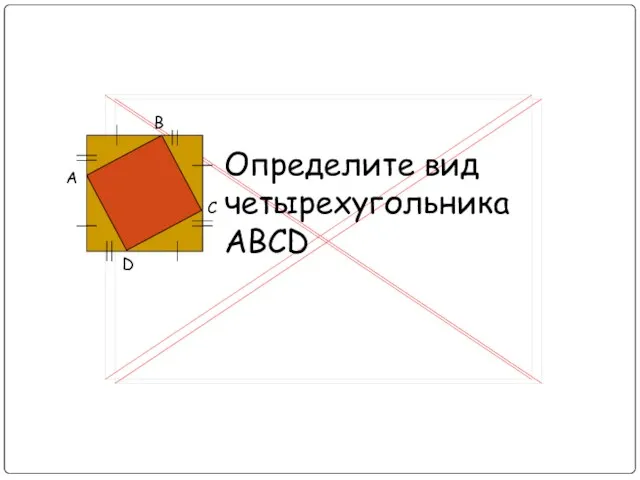
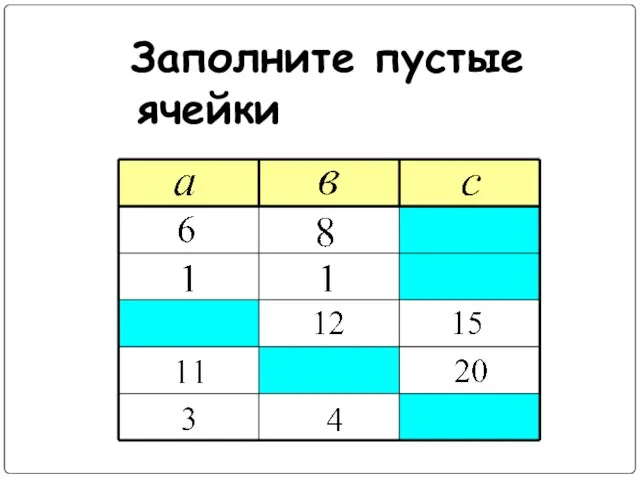
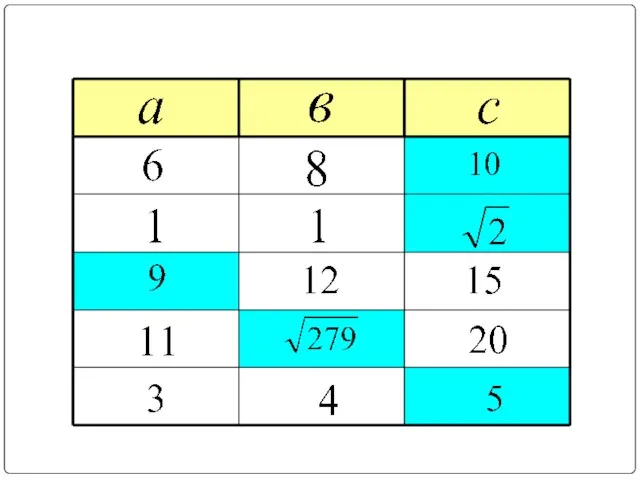
Слайд 3РЕШЕНИЕ:
Найдите площадь АВСD
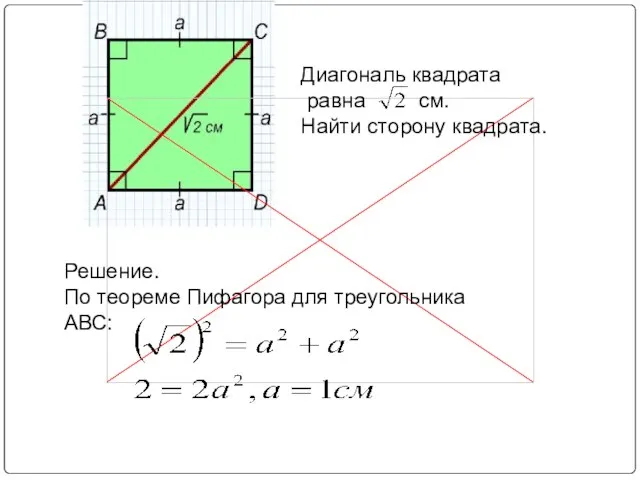
Слайд 6Теорема Пифагора
Из истории
Теорема Пифагора

Слайд 10Рафаэль. Пифагор в окружении учеников.

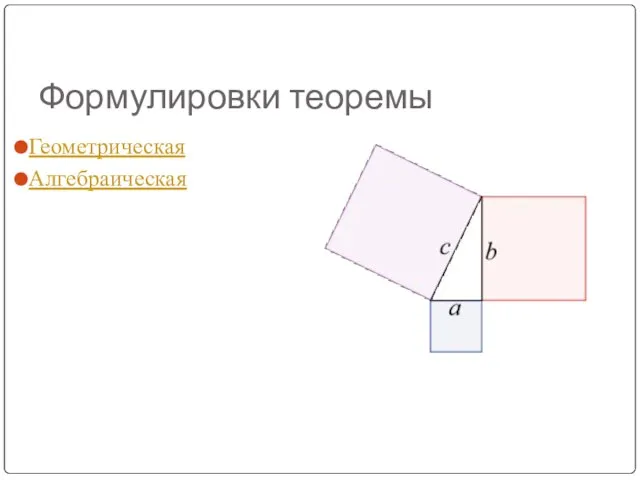
Слайд 11Формулировки теоремы
Геометрическая
Алгебраическая
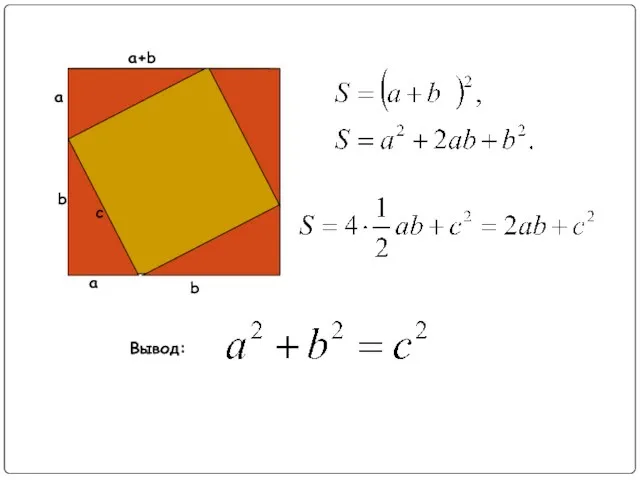
Слайд 12Геометрическая
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов,
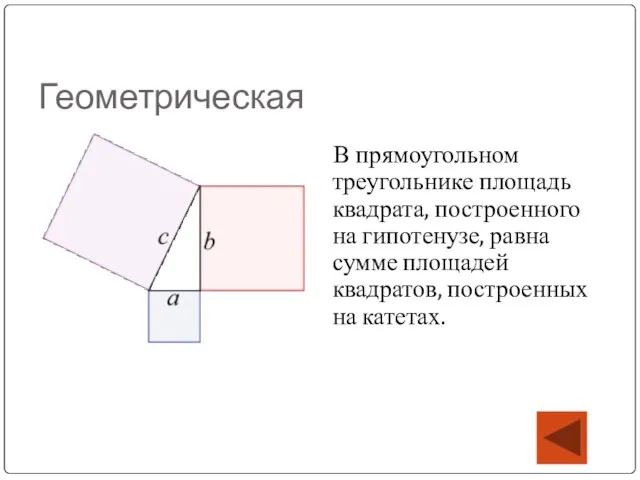
построенных на катетах.
Слайд 13Алгебраическая
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
То

есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b:
Слайд 14Доказательства
В научной литературе зафиксировано 367 доказательств данной теоремы.
Теорема Пифагора является единственной

теоремой со столь внушительным числом доказательств.
Способы доказательства теоремы:
Через подобные треугольники.
Доказательство методом площадей.
Доказательство через равнодополняемость.
Доказательство через равносоставленность.
Доказательство Евклида.
Слайд 15Пифагоровы штаны
Школьное устаревшее шуточное название теоремы Пифагора.
Пифагоровы штаны — на все
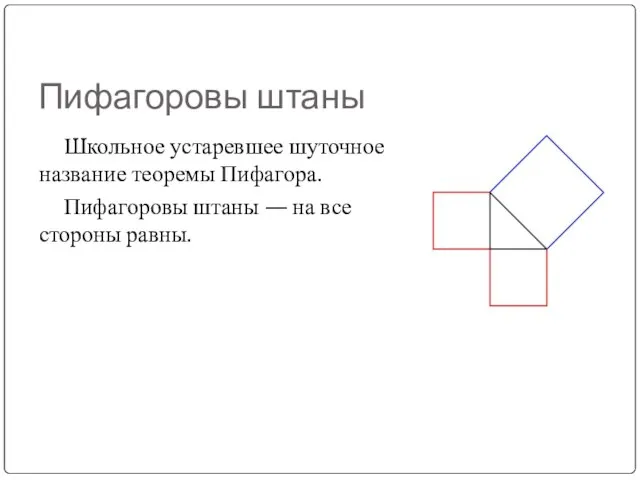
стороны равны.
Слайд 17И .Дырченко
Если дан нам треугольник,
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда

легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим-
И таким простым путем
К результату мы придем.
Слайд 18Самое ценное в математике -
это возможность быстрого приложения теории к практике

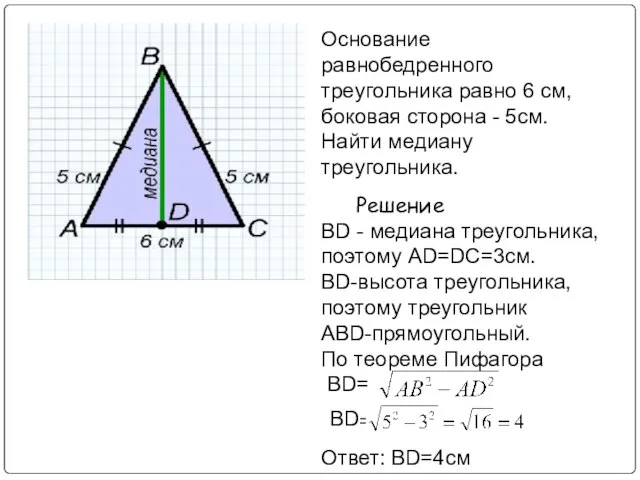
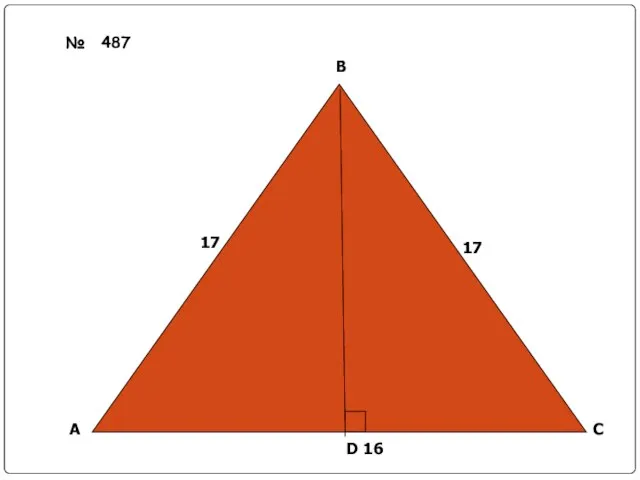
Слайд 21Основание равнобедренного треугольника равно 6 см,
боковая сторона - 5см.
Найти медиану















 Биография Фета
Биография Фета Фондовый рынок
Фондовый рынок Как подготовиться к сочинению-описанию "Весенний парк"
Как подготовиться к сочинению-описанию "Весенний парк" Строение вещества
Строение вещества Специфика изображений в полиграфии (9 класс)
Специфика изображений в полиграфии (9 класс) 27 мая - Общероссийский день библиотек
27 мая - Общероссийский день библиотек Ты Знайка или Незнайка?
Ты Знайка или Незнайка? Храмов Сергей МихайловичЛАТЕНТНАЯ ПРЕСТУПНОСТЬ:МЕТОДОЛОГИЯ ПОЗНАНИЯ И ОСНОВНЫЕ НАПРАВЛЕНИЯ ПРОТИВОДЕЙСТВИЯ
Храмов Сергей МихайловичЛАТЕНТНАЯ ПРЕСТУПНОСТЬ:МЕТОДОЛОГИЯ ПОЗНАНИЯ И ОСНОВНЫЕ НАПРАВЛЕНИЯ ПРОТИВОДЕЙСТВИЯ Урок геометрии по теме «Сумма углов треугольника»
Урок геометрии по теме «Сумма углов треугольника» Швейцарское акционерное общество
Швейцарское акционерное общество  Беспилотная мусорная машина с повышенной маневренностью
Беспилотная мусорная машина с повышенной маневренностью Школы №355
Школы №355 IMPORT & EXPORT PROCEDURES/GUIDELINES
IMPORT & EXPORT PROCEDURES/GUIDELINES  «РАЗРАБОТКА МЕТОДИКИ ПО РАБОТЕ С НАУЧНОЙ ЛИТЕРАТУРОЙ»
«РАЗРАБОТКА МЕТОДИКИ ПО РАБОТЕ С НАУЧНОЙ ЛИТЕРАТУРОЙ» Торговая стратегия Triple Screen
Торговая стратегия Triple Screen Новости на МашДаш ТВ
Новости на МашДаш ТВ Презентация на тему Строение Литосферы
Презентация на тему Строение Литосферы  Презентация на тему Животные Австралии
Презентация на тему Животные Австралии ВИЗИТНАЯ КАРТОЧКА
ВИЗИТНАЯ КАРТОЧКА Урок как основная форма организации учебного процесса. Лекция 3
Урок как основная форма организации учебного процесса. Лекция 3 Футуризм в литературе и искусстве
Футуризм в литературе и искусстве Новобранец. Outcast – 6 episode
Новобранец. Outcast – 6 episode Познание, как особая сторона взаимодействия человека с окружающим миром. Классификации психических процессов
Познание, как особая сторона взаимодействия человека с окружающим миром. Классификации психических процессов Опорно-двигательная система
Опорно-двигательная система Что общего?
Что общего? Бородинская битва
Бородинская битва Национальная Ассоциация Предприятий Технического Обслуживания и Ремонта Автомототранспортных Средств
Национальная Ассоциация Предприятий Технического Обслуживания и Ремонта Автомототранспортных Средств Секреты управления своими эмоциями
Секреты управления своими эмоциями