Содержание
- 2. Цель урока: Повторить теорему Пифагора; Применять теорему Пифагора при решении простейших задач геометрии; Рассмотреть исторические задачи;
- 4. Без преувеличения можно сказать, что его теорема самая известная теорема геометрии, ибо о ней знает подавляющее
- 5. В чем же причина такой популярности Теоремы Пифагора Знатоки утверждают, что причин здесь три: б) красота,
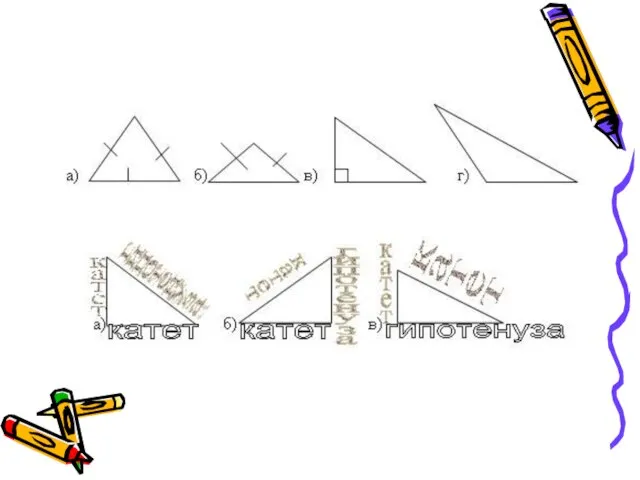
- 7. Гипотенуза больше катета. Сумма острых углов прямоугольного треугольника равна 1800. Площадь прямоугольного треугольника с катетами а
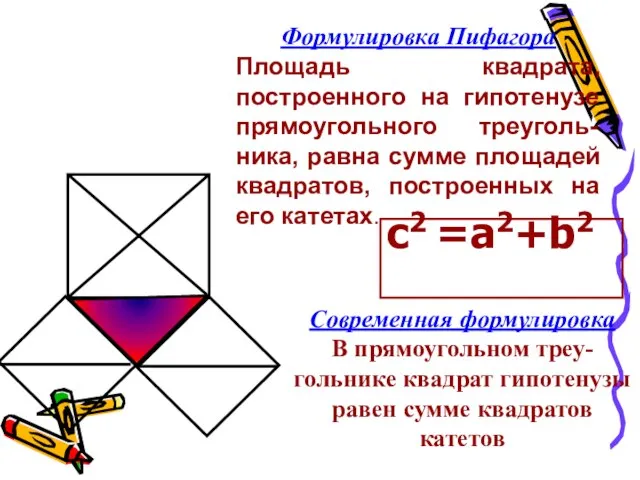
- 8. Формулировка Пифагора Площадь квадрата, построенного на гипотенузе прямоугольного треуголь-ника, равна сумме площадей квадратов, построенных на его
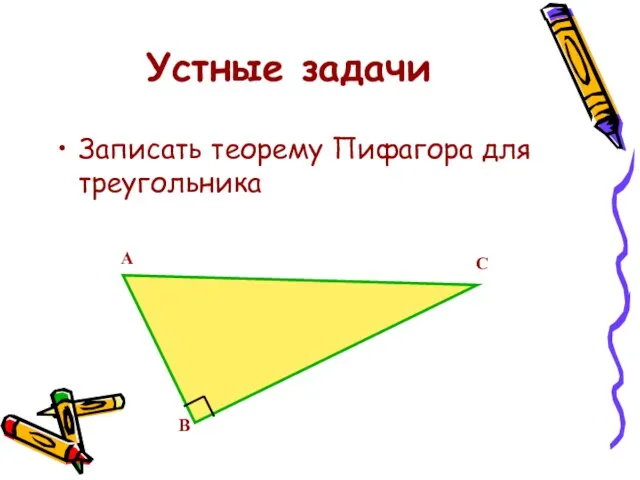
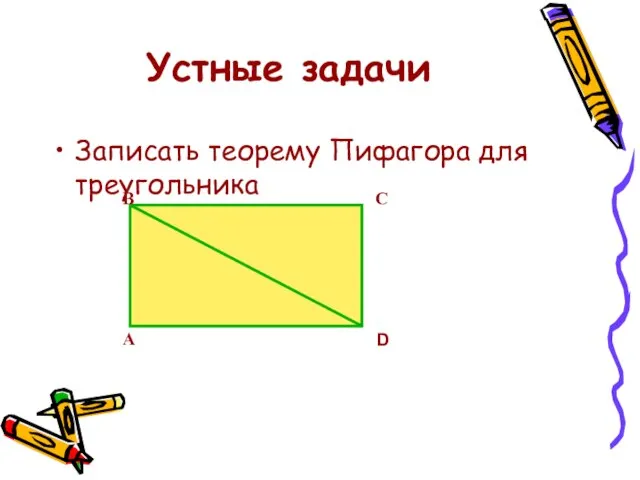
- 9. Устные задачи Записать теорему Пифагора для треугольника А В С
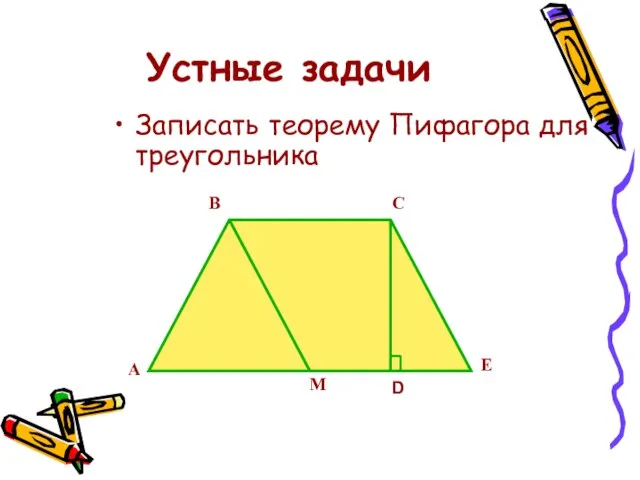
- 10. Устные задачи Записать теорему Пифагора для треугольника А В С Е D М
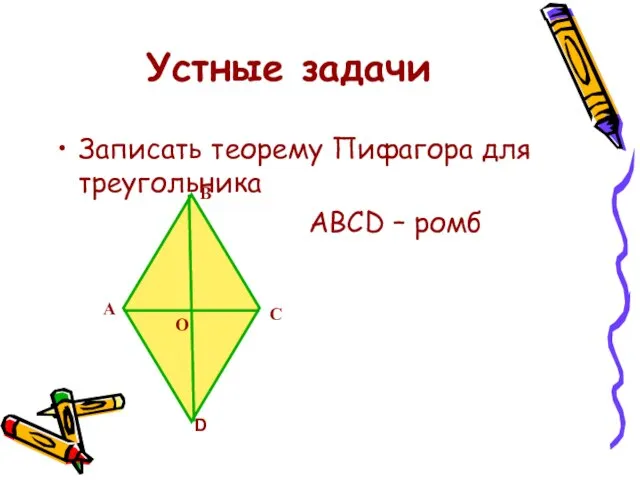
- 11. Устные задачи Записать теорему Пифагора для треугольника АВСD – ромб А В С D О
- 12. Устные задачи Записать теорему Пифагора для треугольника А В С D
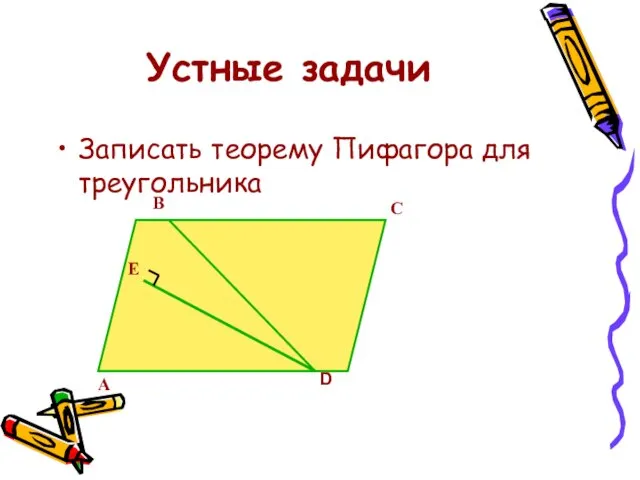
- 13. Устные задачи Записать теорему Пифагора для треугольника А В С D Е
- 14. Алгоритм решения задач с применением теоремы Пифагора Указать прямоугольный треугольник; Записать для него теорему Пифагора; с2
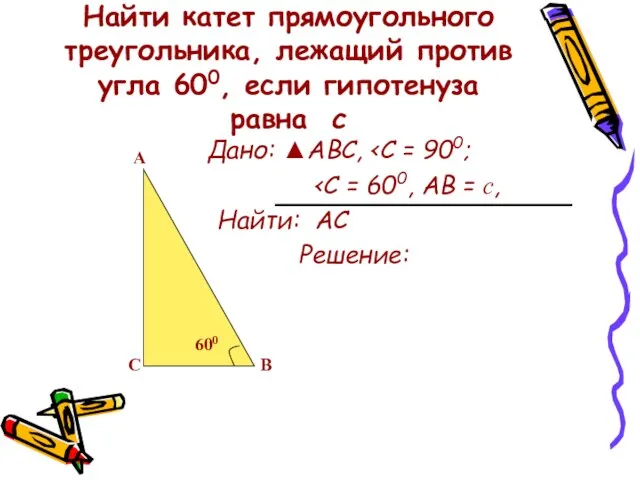
- 15. Найти катет прямоугольного треугольника, лежащий против угла 600, если гипотенуза равна с Дано: ▲АВС, Найти: АС
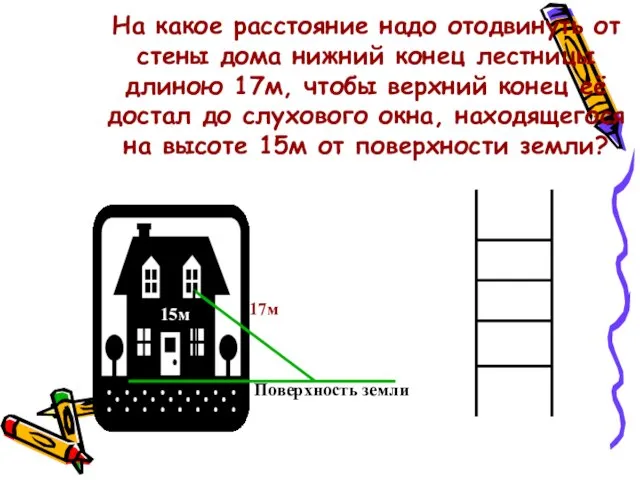
- 16. На какое расстояние надо отодвинуть от стены дома нижний конец лестницы длиною 17м, чтобы верхний конец
- 17. На какое расстояние надо отодвинуть от стены дома нижний конец лестницы длиною 17м, чтобы верхний конец
- 18. Задача древних индусов Над озером тихим, С полфута размером, высился лотоса цвет. Он рос одиноко. И
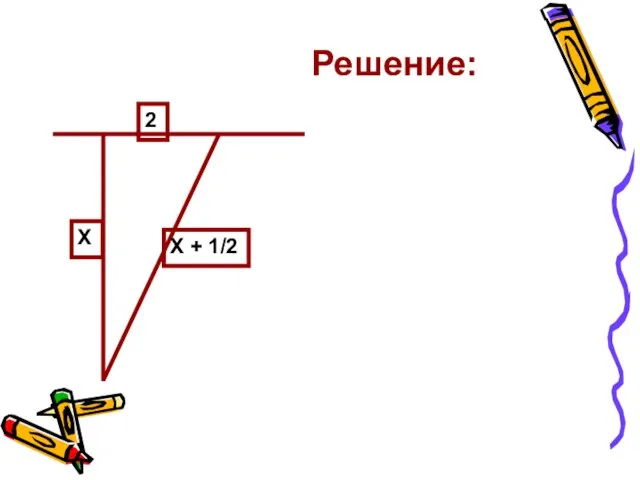
- 19. Решение:
- 20. На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И
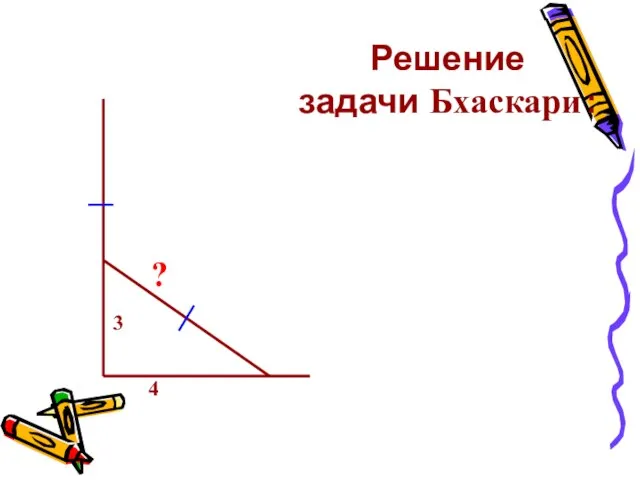
- 21. Решение задачи Бхаскари : 3 4 ?
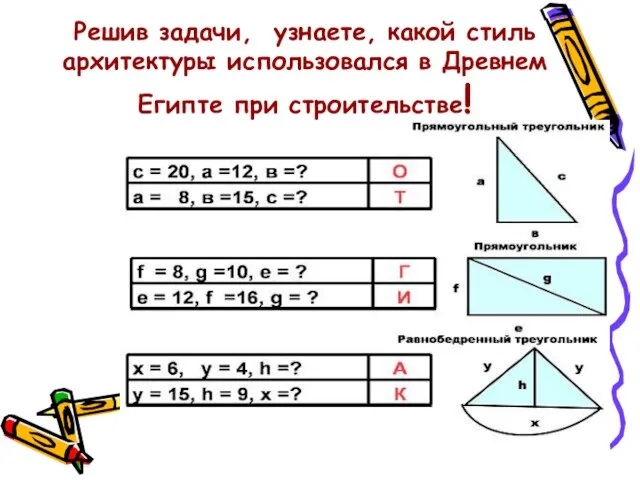
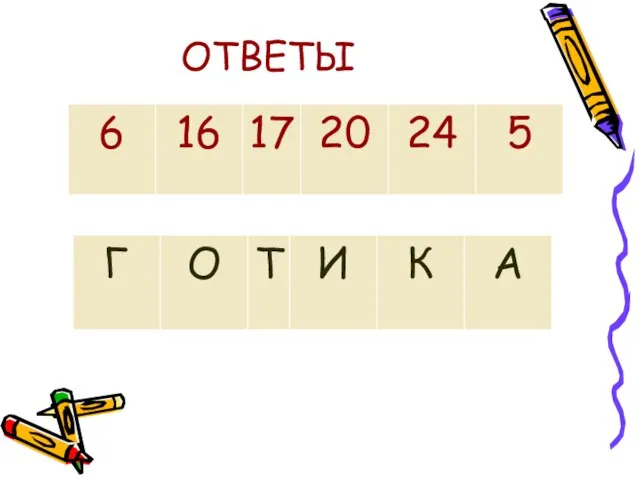
- 22. Решив задачи, узнаете, какой стиль архитектуры использовался в Древнем Египте при строительстве!
- 23. ОТВЕТЫ
- 24. Собор Парижской Богоматери
- 25. Домашнее задание: Повторить п.48 - 55 «5» - задача №499 «4» - задача №498 «3» -задача
- 26. Итог урока «Сегодня на уроке я повторил…» «Сегодня на уроке я узнал…» «Сегодня на уроке я
- 27. Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли ее так же “ветряной мельницей”, составляли стихи вроде “Пифагоровы
- 28. Теорема Пифагора Итак, Если дан нам треугольник, И притом с прямым углом, То квадрат гипотенузы Мы
- 29. успешно усвоил теорему Пифагора, выполнил все задания, стал участником открытого урока и еще раз убедился в
- 31. Скачать презентацию















 Организация как функция менеджмента
Организация как функция менеджмента Изучение типологических особенностей спортсменов разной специализации
Изучение типологических особенностей спортсменов разной специализации Дуализм доменного имени: домен как объект и как орудие правонарушения в Интернете Андрей Воробьев, Директор департамента PR
Дуализм доменного имени: домен как объект и как орудие правонарушения в Интернете Андрей Воробьев, Директор департамента PR  Основные направления моды в парикмахерском искусстве. Самостоятельная работа №1
Основные направления моды в парикмахерском искусстве. Самостоятельная работа №1 Достижения • Победители краевого конкурса Re=0 Не участвовали (?) лучших учителей края • Победители краевого конкурса
Достижения • Победители краевого конкурса Re=0 Не участвовали (?) лучших учителей края • Победители краевого конкурса  Легенды о головоломках
Легенды о головоломках Интернет – образование
Интернет – образование Чудесные превращения воды в природе
Чудесные превращения воды в природе Здоровье в школе
Здоровье в школе Игра-тренинг Денежный поток. Основы финансовой грамотности, грамотное обращение с личными финансами, навыки инвестирования
Игра-тренинг Денежный поток. Основы финансовой грамотности, грамотное обращение с личными финансами, навыки инвестирования Verbs 3
Verbs 3 Аутэкология. Факторная экология
Аутэкология. Факторная экология Практикум по методам психологического исследования. Лабораторное занятие № 1
Практикум по методам психологического исследования. Лабораторное занятие № 1 Применение современных моделей автоматизации в профессиональной деятельности повара, кондитера
Применение современных моделей автоматизации в профессиональной деятельности повара, кондитера Системы ограждений на винтовых фундаментах в условиях городской среды
Системы ограждений на винтовых фундаментах в условиях городской среды Globas presentation
Globas presentation Radiomics: Extracting more Features using Endoscopic Imaging
Radiomics: Extracting more Features using Endoscopic Imaging Заимствованные слова
Заимствованные слова бізнесмен
бізнесмен Островский как основоположник русского театра
Островский как основоположник русского театра Тестирование рыночных ниш и стратегия продвижения
Тестирование рыночных ниш и стратегия продвижения Права ребёнка 4-6 класс
Права ребёнка 4-6 класс Презентация на тему Чарушин "Страшный рассказ"
Презентация на тему Чарушин "Страшный рассказ" Презентация на тему Молоко и его свойства
Презентация на тему Молоко и его свойства Социальные сети Презентацию разработала ученица 11 класса «А» Рязанова Анастасия.
Социальные сети Презентацию разработала ученица 11 класса «А» Рязанова Анастасия. Презентация на тему Первичная обработка овощей
Презентация на тему Первичная обработка овощей Команда
Команда