Содержание
- 2. Актуальность разработки обусловлена возрастающей сложностью задач, которые ставятся перед разработчиками информационных технологий, повышением требований к скорости
- 3. Аналитические: Теория динамических систем (Mathcad, Matlab) Теория автоматического управления (Simulink) Системная динамика (Vensim, Powersim) Теория случайных
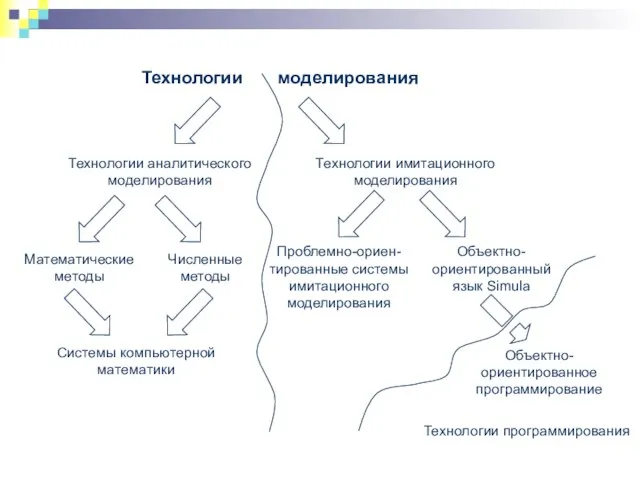
- 4. Технологии моделирования Технологии аналитического моделирования Технологии имитационного моделирования Проблемно-ориен-тированные системы имитационного моделирования Объектно-ориентированный язык Simula Объектно-ориентированное
- 5. Сети Петри как средство формализации дискретно-событийных процессов управления Преимущества сетей Петри Высокий уровень формализации дискретно-событийных систем
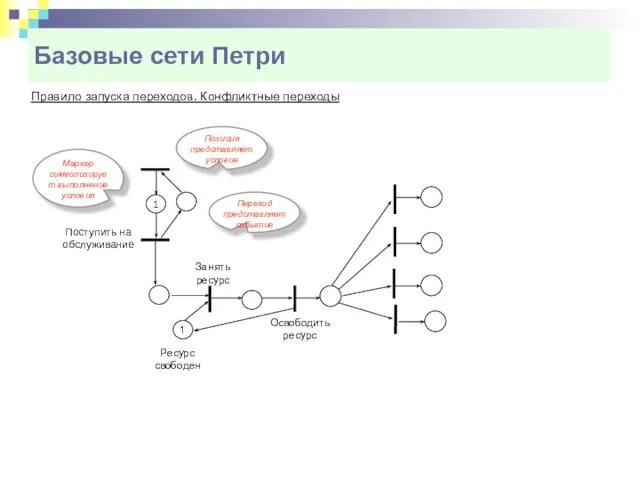
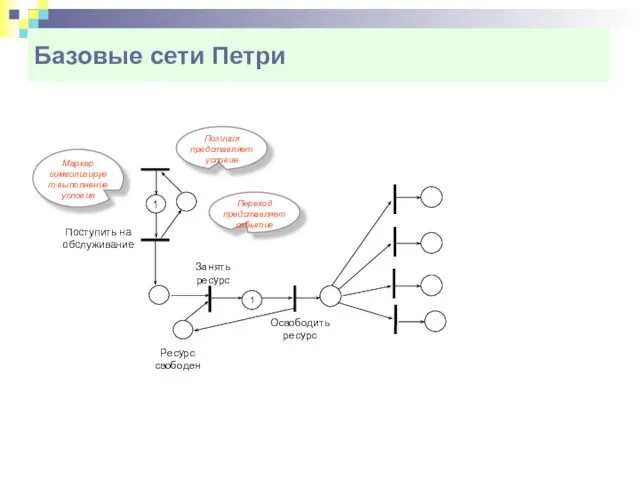
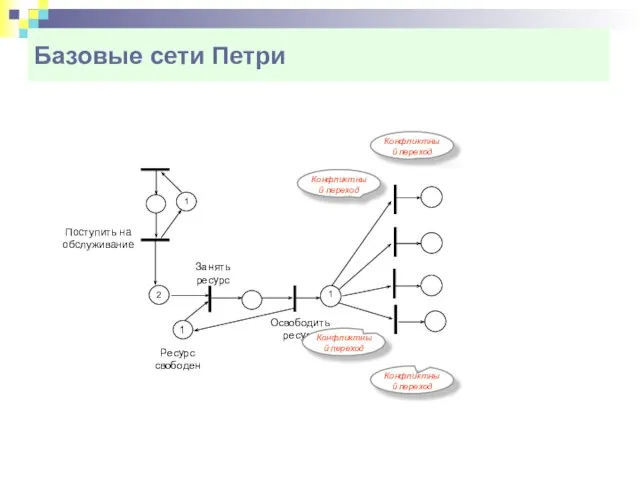
- 6. Базовые сети Петри Правило запуска переходов. Конфликтные переходы
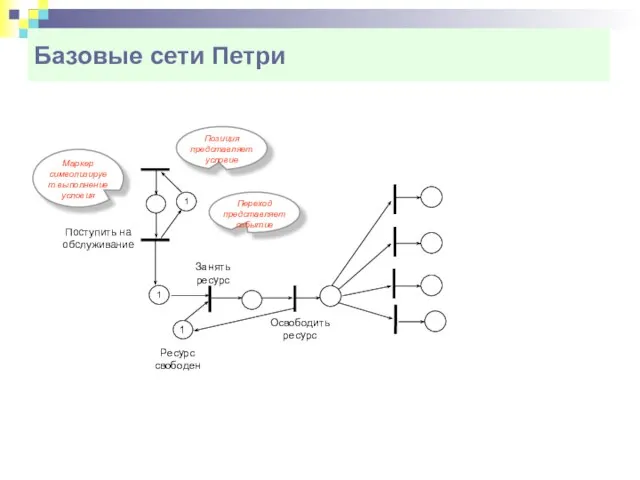
- 7. Базовые сети Петри
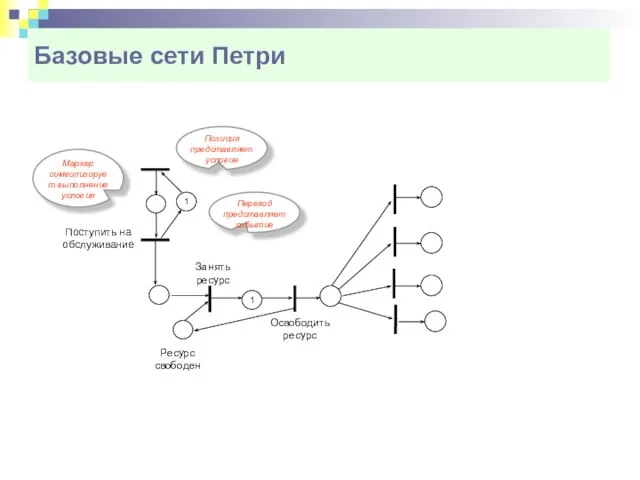
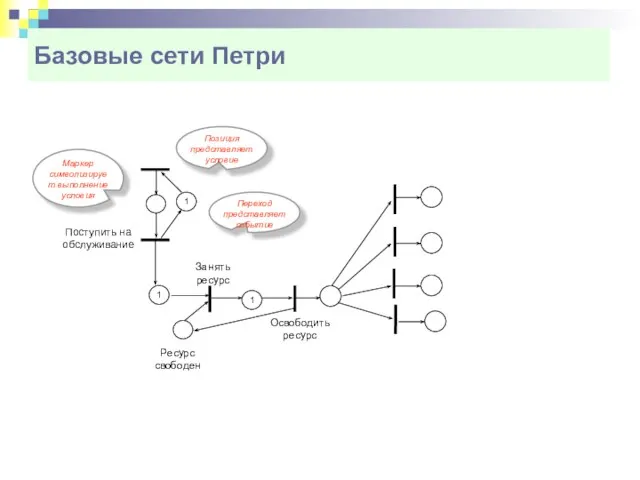
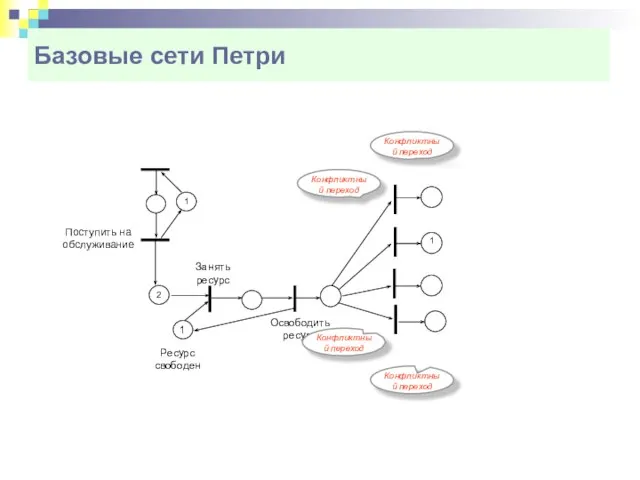
- 8. Базовые сети Петри
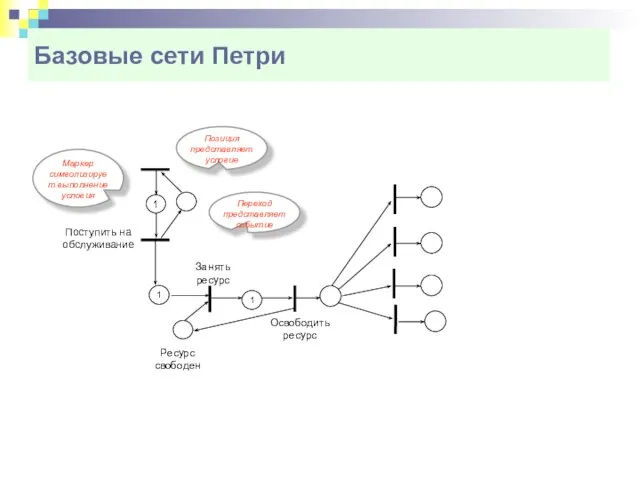
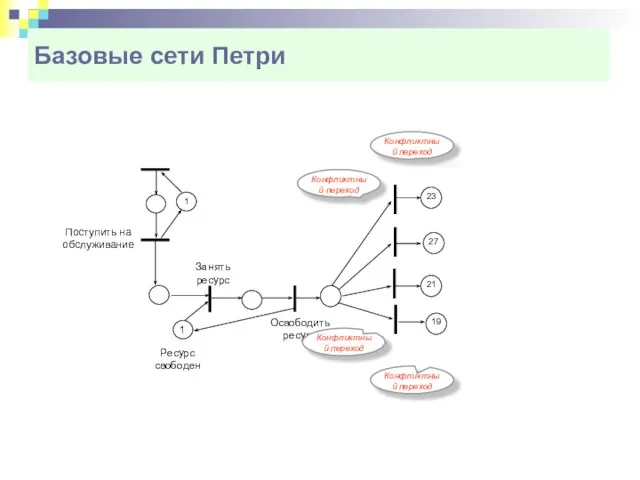
- 9. Базовые сети Петри
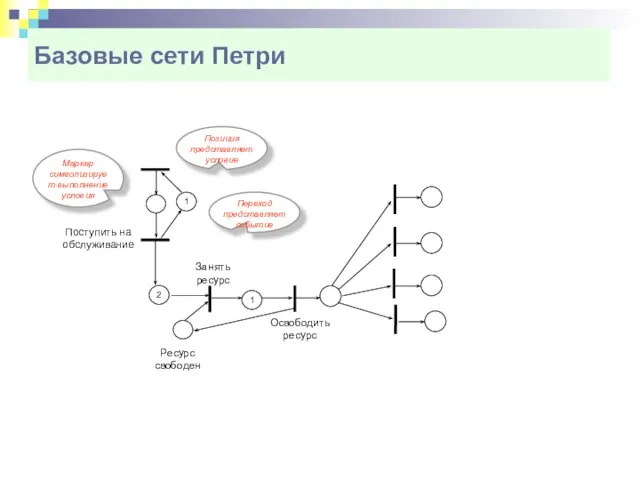
- 10. Базовые сети Петри
- 11. Базовые сети Петри
- 12. Базовые сети Петри
- 13. Базовые сети Петри
- 14. Базовые сети Петри
- 15. Базовые сети Петри
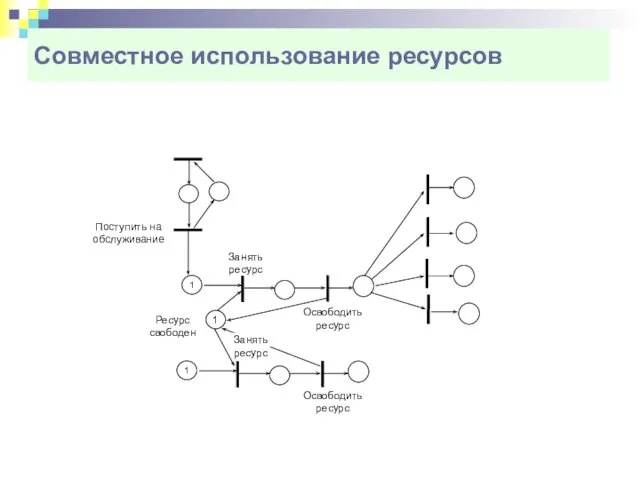
- 16. Совместное использование ресурсов
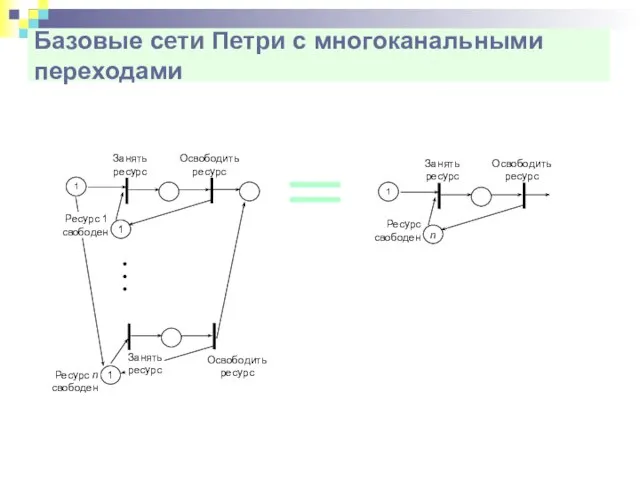
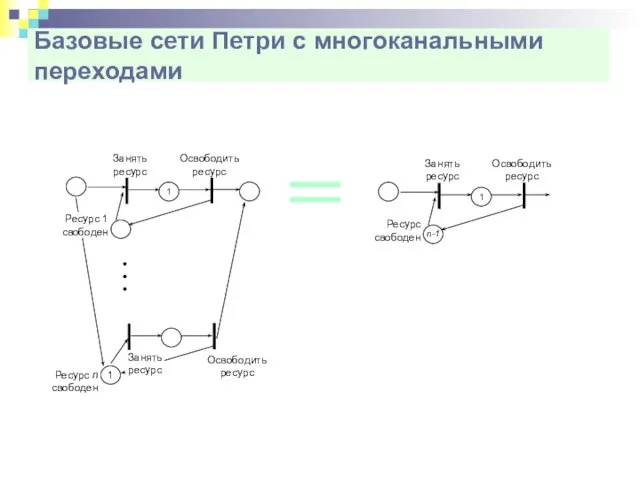
- 17. Базовые сети Петри с многоканальными переходами
- 18. Базовые сети Петри с многоканальными переходами
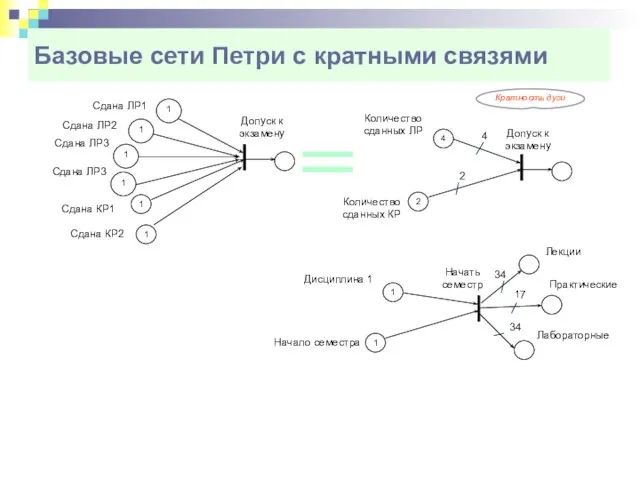
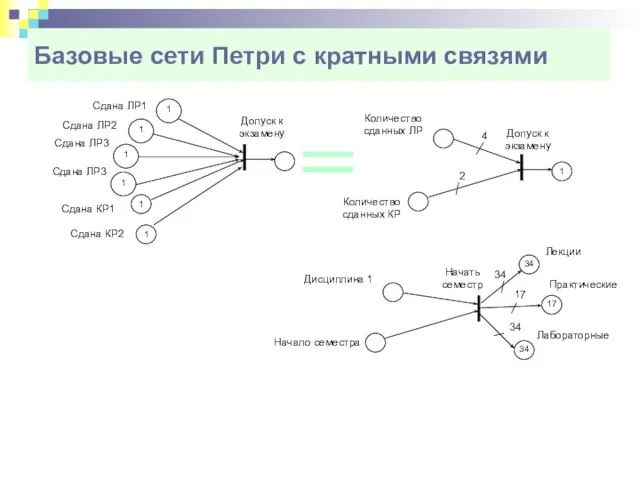
- 19. Базовые сети Петри с кратными связями Кратность дуги
- 20. Базовые сети Петри с кратными связями
- 21. - множество дуг - кратности дуг - множество переходов - множество позиций Математическое описание базовой сети
- 22. Матричные уравнения состояний базовой сети Петри Фундаментальное уравнение состояний базовой сети Петри: - вектор количества запусков
- 23. Теория базовых сетей Петри Классификация сетей Петри: безопасные, ординарные, автоматные и др. Аналитическое исследование свойств модели
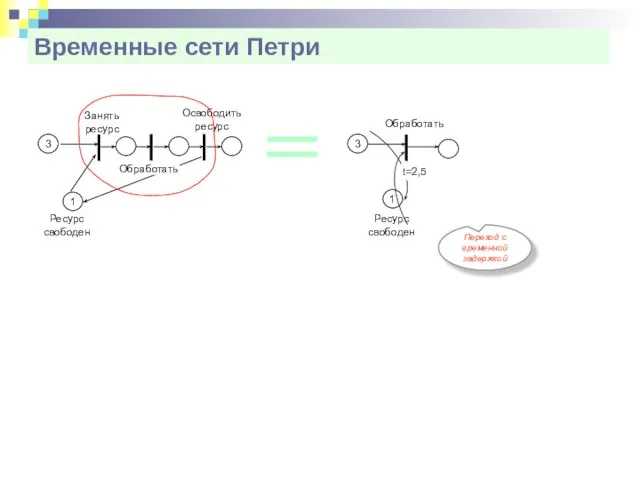
- 24. Временные сети Петри Переход с временной задержкой Занять ресурс 3 1 Освободить ресурс Ресурс свободен Обработать
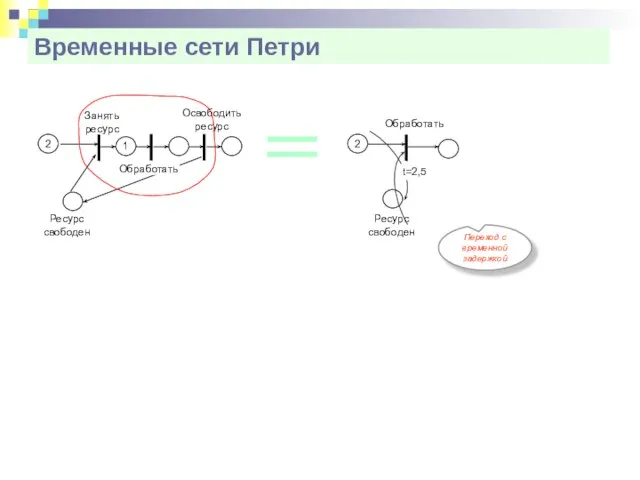
- 25. Временные сети Петри Переход с временной задержкой Занять ресурс 2 1 Освободить ресурс Ресурс свободен Обработать
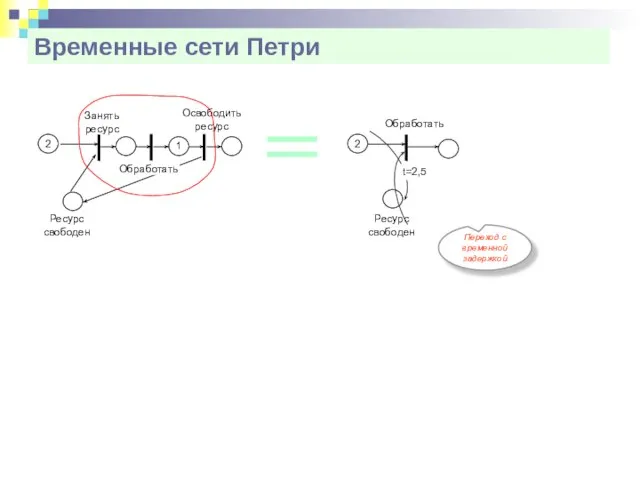
- 26. Временные сети Петри Переход с временной задержкой Занять ресурс 2 Освободить ресурс Ресурс свободен 1 Обработать
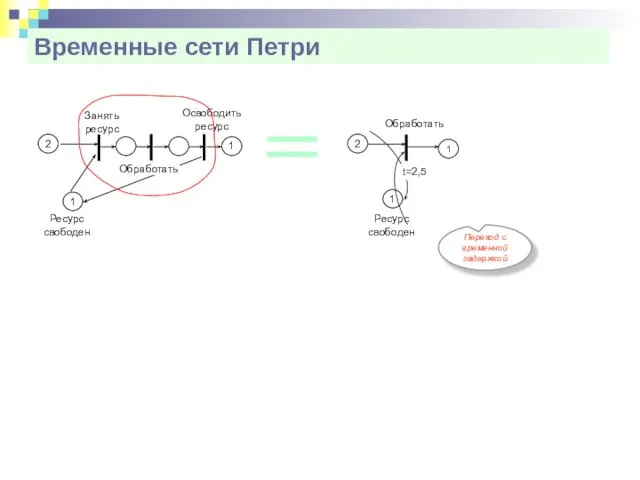
- 27. Временные сети Петри Переход с временной задержкой Занять ресурс 2 1 Освободить ресурс Ресурс свободен 1
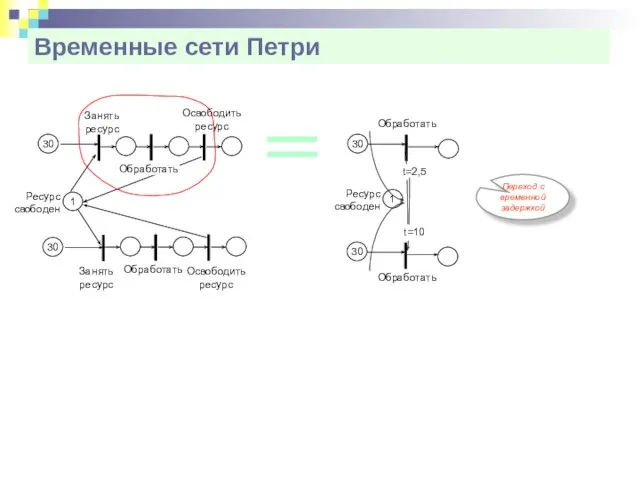
- 28. Временные сети Петри Переход с временной задержкой Обработать 30 1 Ресурс свободен t=2,5 Занять ресурс 30
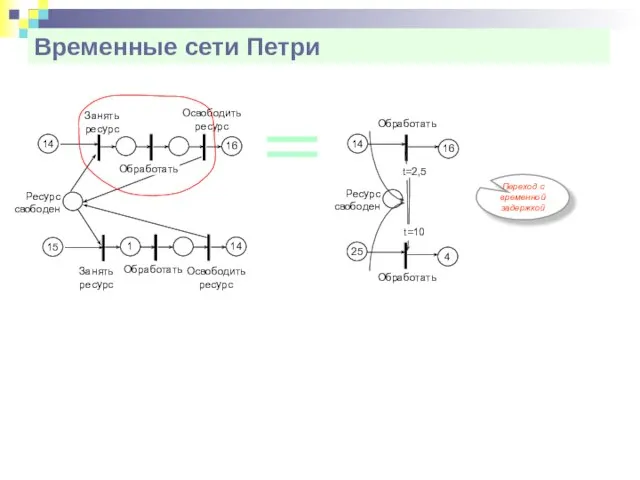
- 29. Временные сети Петри Переход с временной задержкой Обработать 14 16 Ресурс свободен t=2,5 Занять ресурс 14
- 30. Теория временных сетей Петри Классификация, исследование свойств Wang J. Timed Petri Nets: Theory and Application /
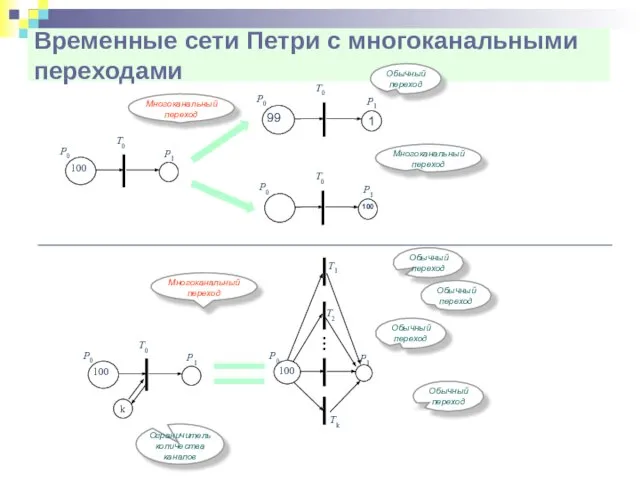
- 31. Временные сети Петри с многоканальными переходами Многоканальный переход Обычный переход Обычный переход Обычный переход Обычный переход
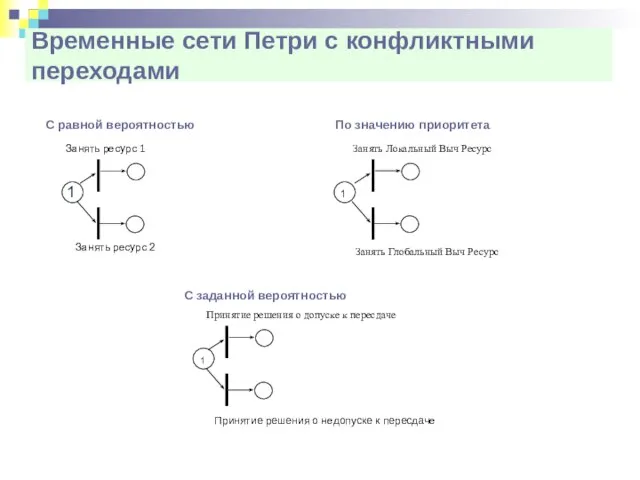
- 32. Временные сети Петри с конфликтными переходами С равной вероятностью По значению приоритета С заданной вероятностью Принятие
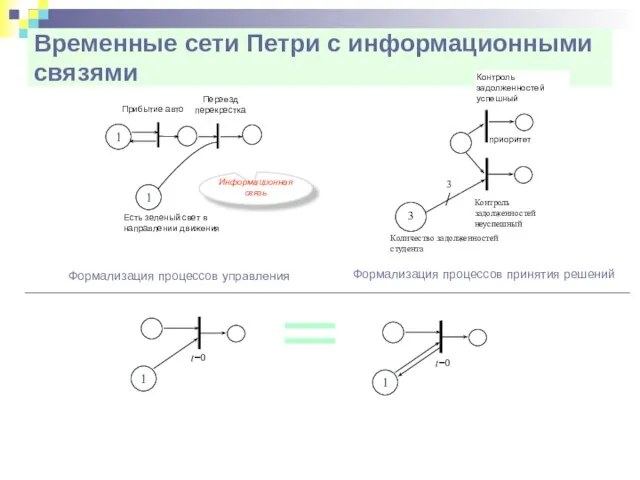
- 33. Временные сети Петри с информационными связями Количество задолженностей студента 3 Контроль задолженностей неуспешный Контроль задолженностей успешный
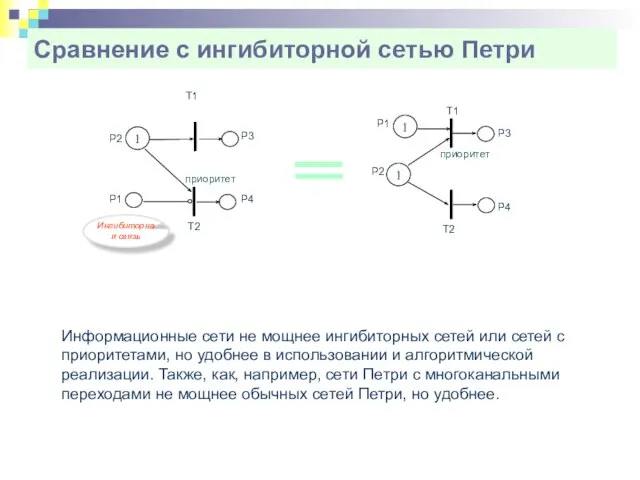
- 34. Сравнение с ингибиторной сетью Петри Т1 Информационные сети не мощнее ингибиторных сетей или сетей с приоритетами,
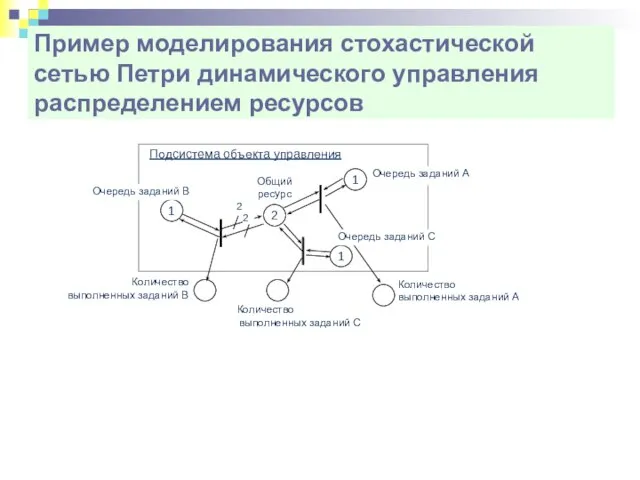
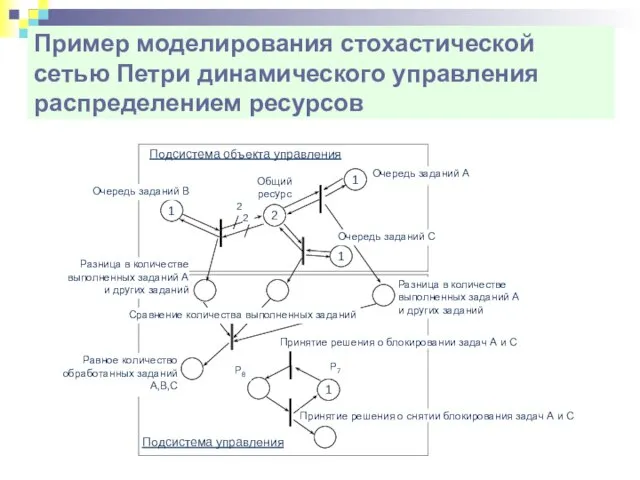
- 35. Пример моделирования стохастической сетью Петри динамического управления распределением ресурсов Подсистема объекта управления 2 2 2 1
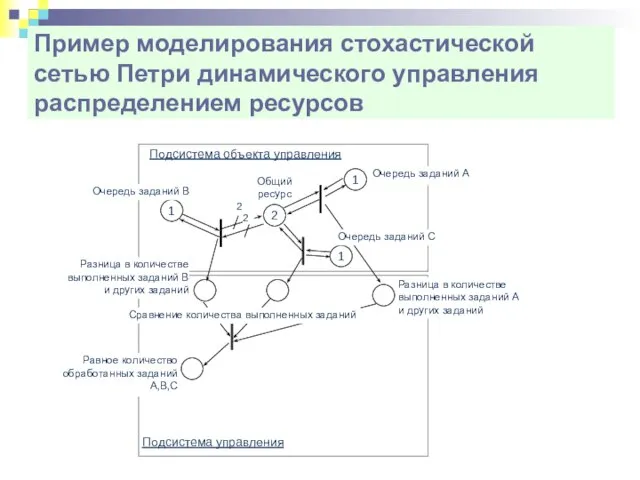
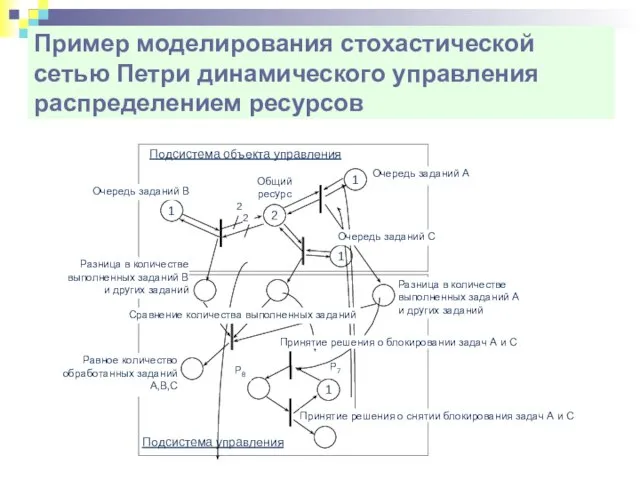
- 36. Пример моделирования стохастической сетью Петри динамического управления распределением ресурсов Подсистема объекта управления Подсистема управления 2 2
- 37. Пример моделирования стохастической сетью Петри динамического управления распределением ресурсов Подсистема объекта управления Подсистема управления 2 2
- 38. Пример моделирования стохастической сетью Петри динамического управления распределением ресурсов Подсистема объекта управления Подсистема управления 2 2
- 39. Уравнения состояний детерминированной временной сети Петри с конфликтными и многоканальными переходами [Зайцев Д.А. Инварианты временных сетей
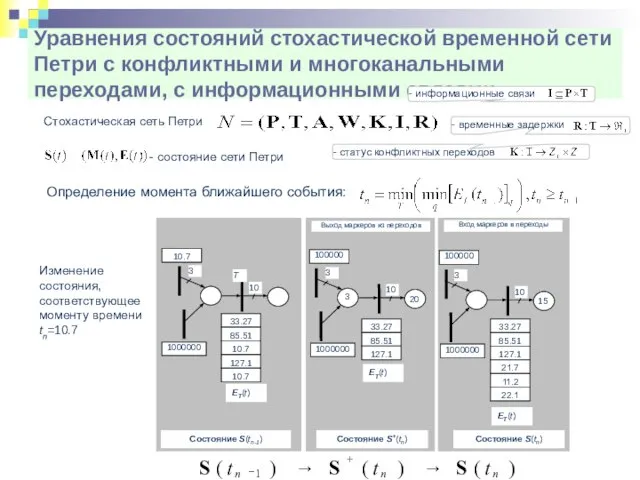
- 40. - временные задержки Уравнения состояний стохастической временной сети Петри с конфликтными и многоканальными переходами, с информационными
- 41. Преобразование сети Петри, соответствующее выходу маркеров из переходов
- 42. Преобразование сети Петри, соответствующее входу маркеров в переходы где
- 43. Преобразование сети Петри, соответствующее m-кратному входу маркеров в переходы
- 44. Уравнения состояний стохастической временной сети Петри с конфликтными и многоканальными переходами, с информационными связями
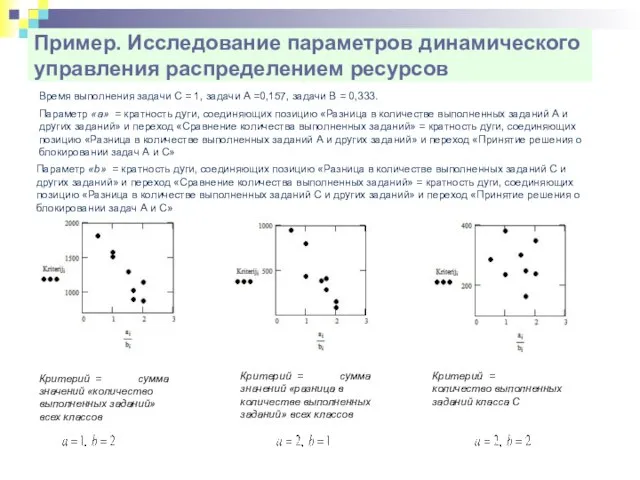
- 45. Пример. Исследование параметров динамического управления распределением ресурсов Параметр «a» = кратность дуги, соединяющих позицию «Разница в
- 46. Матричные уравнения состояний стохастической временной сети Петри с конфликтными и многоканальными переходами, с информационными связями
- 47. Сравнение матричных уравнений состояний стохастической временной сети Петри с известными уравнениями состояний сети Петри ⇒ Фундаментальное
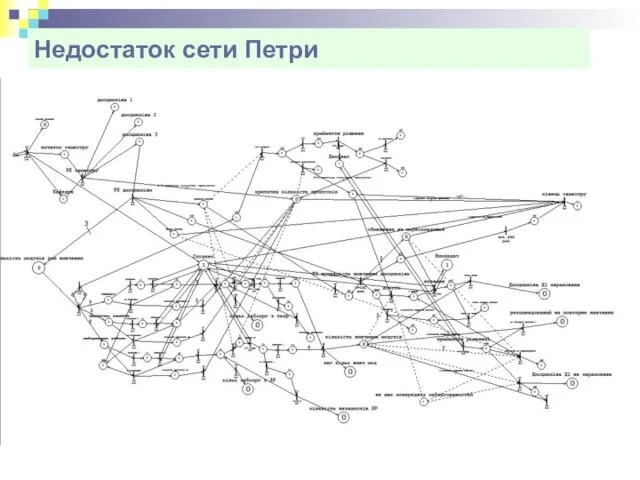
- 48. Недостаток сети Петри
- 49. ООП и сети Петри Блочная структура сети Петри [Ямпольський Л.С., Лавров О.А. Штучний інтелект у плануванні
- 50. Понятие Петри-объекта Поле Сеть Петри Поле Время моделирования Поле Текущий момент времени Метод Выполнить статистические вычисления
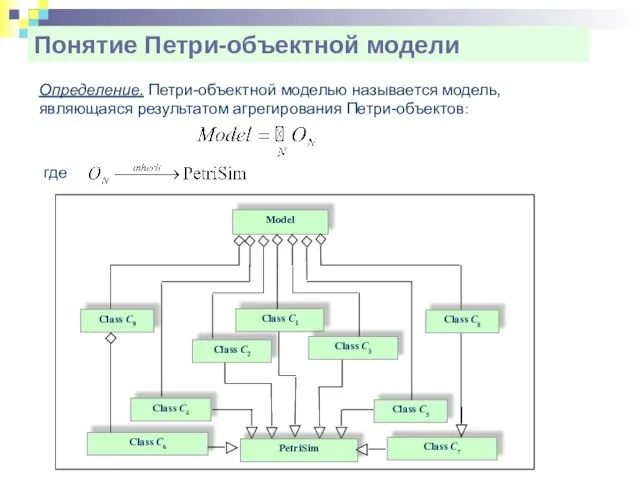
- 51. Понятие Петри-объектной модели Определение. Петри-объектной моделью называется модель, являющаяся результатом агрегирования Петри-объектов: Class C2 Class C1
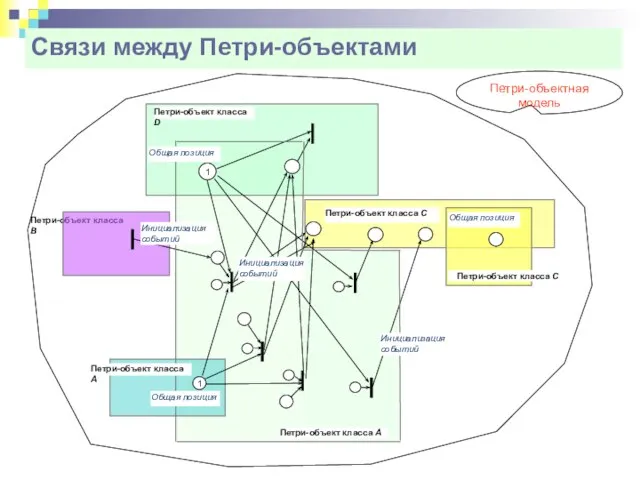
- 52. Связи между Петри-объектами
- 53. Утверждение 1 Петри-объектная модель описывается стохастической временной сетью Петри, являющейся объединением сетей Петри-объектов, из которых она
- 54. Преобразование сети Петри-объектной модели эквивалентно преобразованию сетей Петри-объектов Следствие. Состояние Петри-объектной модели, являющееся результатом выхода маркеров
- 55. Преобразование сети Петри-объектной модели эквивалентно преобразованию сетей Петри-объектов Следствие. Состояние Петри-объектной модели, являющееся результатом входа маркеров
- 56. Следствие. Состояние Петри-объектной модели в каждый момент времени описывается состоянием ее Петри-объектов. Уравнения состояний Петри-объектной модели
- 57. Формировать список Петри-объектов; Осуществить преобразование (метод Start()); Пока не достигнут момент окончания моделирования продвинуть время в
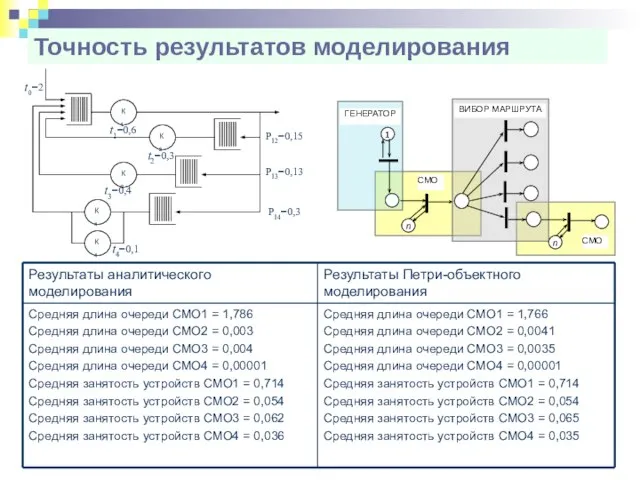
- 58. Точность результатов моделирования
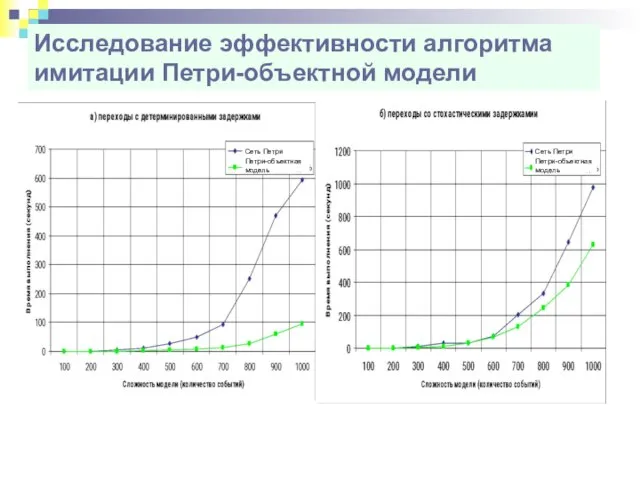
- 59. Исследование эффективности алгоритма имитации Петри-объектной модели
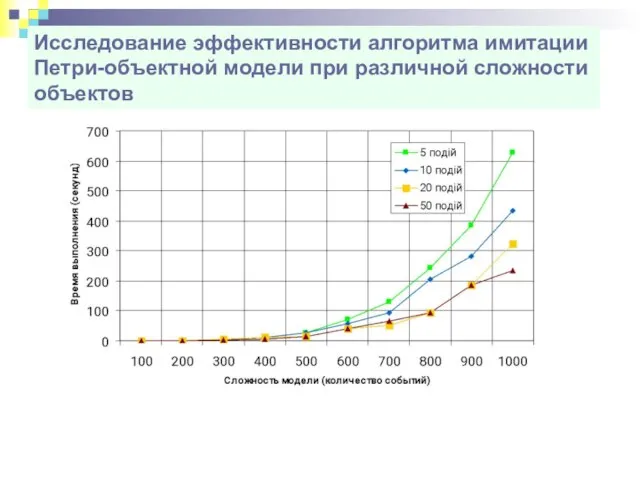
- 60. Исследование эффективности алгоритма имитации Петри-объектной модели при различной сложности объектов
- 61. Петри-объектная модель - это средство формального описания систем, которое: имеет математическое описание, а следовательно, имеет большую
- 62. Практическое применение Петри-объектного моделирования Моделирование систем управления (учебный процесс, транспортные системы) Моделирование параллельных вычислений (грид-системы) Моделирование
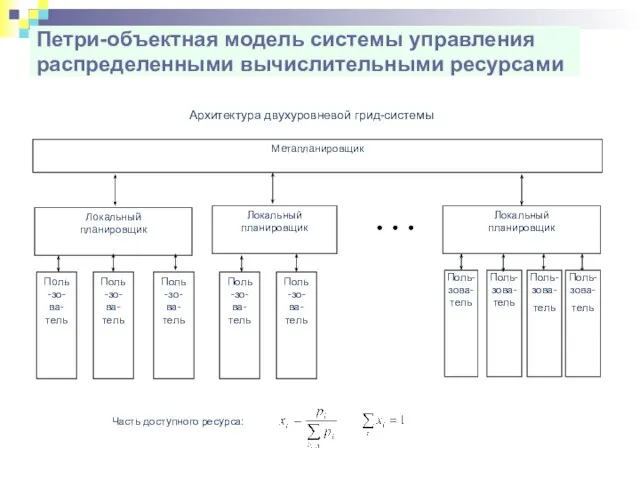
- 63. Петри-объектная модель системы управления распределенными вычислительными ресурсами Метапланировщик Локальный планировщик Локальный планировщик Локальный планировщик Архитектура двухуровневой
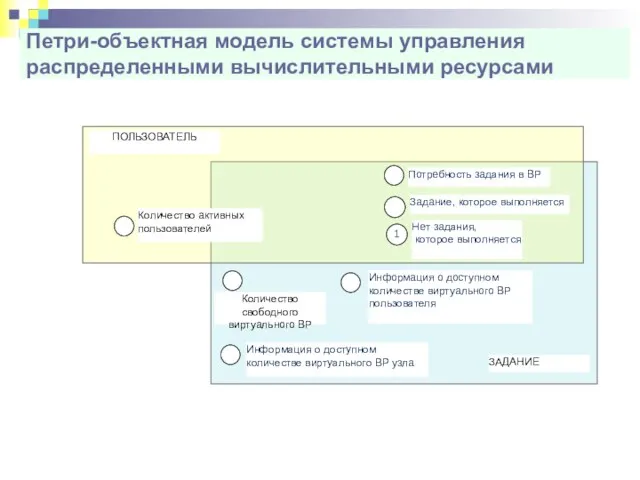
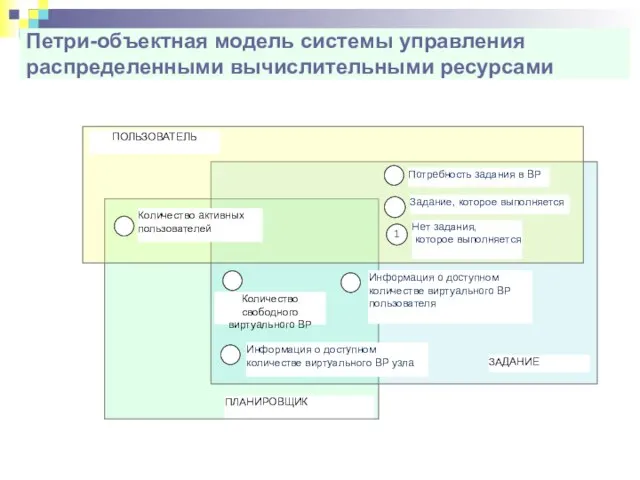
- 64. Петри-объектная модель системы управления распределенными вычислительными ресурсами Количество активных пользователей ПОЛЬЗОВАТЕЛЬ А Потребность задания в ВР
- 65. Петри-объектная модель системы управления распределенными вычислительными ресурсами ЗАДАНИЕ Количество свободного виртуального ВР Количество активных пользователей ПОЛЬЗОВАТЕЛЬ
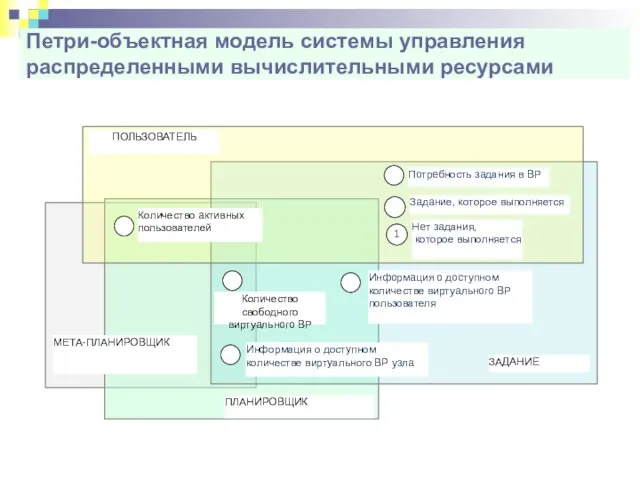
- 66. Петри-объектная модель системы управления распределенными вычислительными ресурсами ЗАДАНИЕ Количество свободного виртуального ВР Количество активных пользователей ПЛАНИРОВЩИК
- 67. Петри-объектная модель системы управления распределенными вычислительными ресурсами
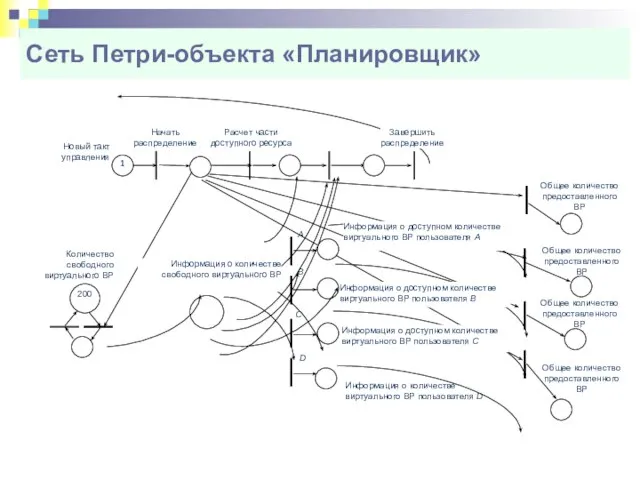
- 68. Сеть Петри-объекта «Планировщик»
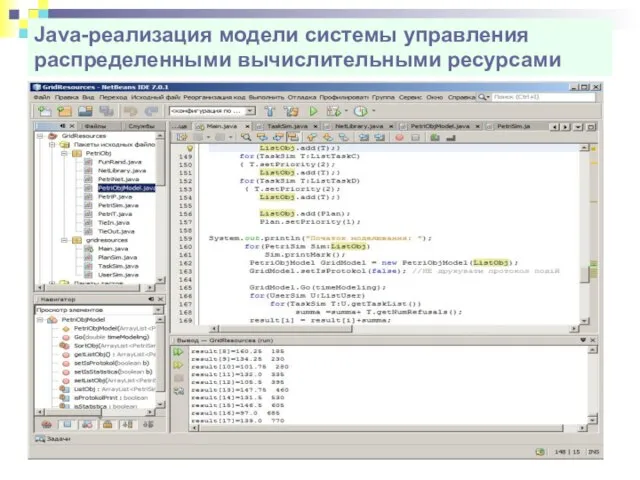
- 69. Java-реализация модели системы управления распределенными вычислительными ресурсами
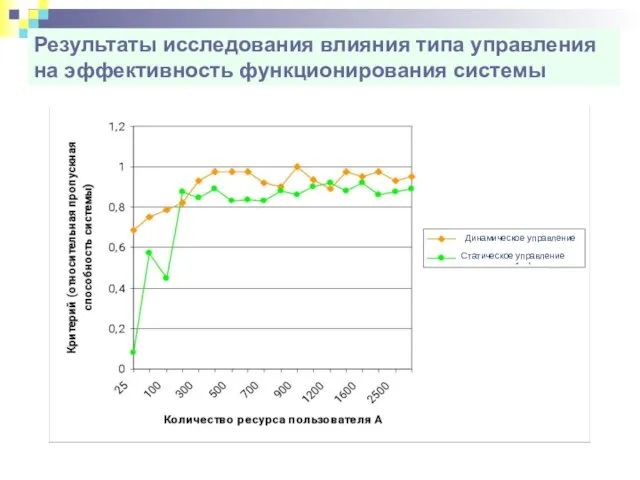
- 70. Результаты исследования влияния типа управления на эффективность функционирования системы
- 71. Заключение Разработаны теоретические основы новой технологии моделирования систем, объединяющей в себе объектно-ориентированную технологию и технологию имитационного
- 73. Скачать презентацию

























 Грамматическая семантика
Грамматическая семантика Разработка проектов и заявок на гранты. Фандрайзинг
Разработка проектов и заявок на гранты. Фандрайзинг Если добрый ты...
Если добрый ты... (“Big read”) «Большое чтение» в Новосибирске
(“Big read”) «Большое чтение» в Новосибирске PowerPoint Title
PowerPoint Title  Literat_Perm (1)
Literat_Perm (1) Click to edit Master title style Click to edit Master subtitle style
Click to edit Master title style Click to edit Master subtitle style  Тема: Государство и его признаки.
Тема: Государство и его признаки. Название бизнес идеи
Название бизнес идеи Презентация на тему Виховна година Ми за здоровий спосіб життя
Презентация на тему Виховна година Ми за здоровий спосіб життя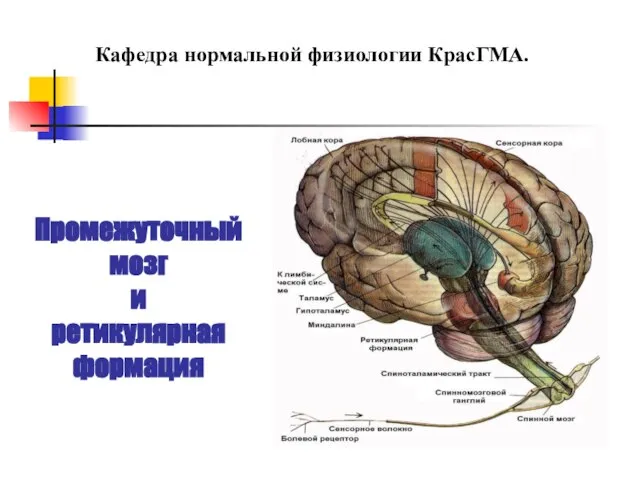 Физиология межуточного мозга
Физиология межуточного мозга образец презентации ИАР
образец презентации ИАР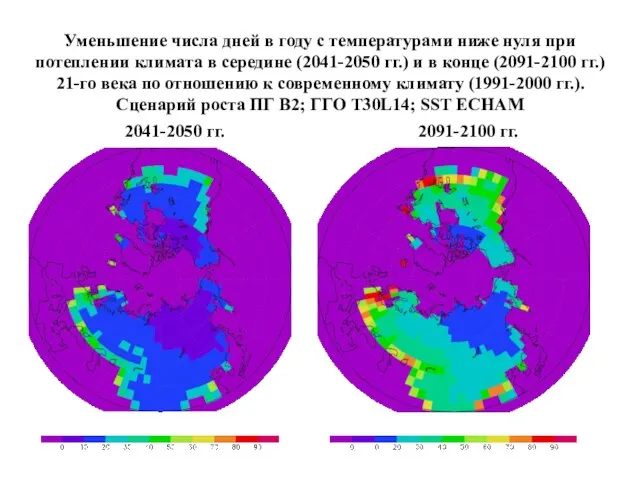 Уменьшение числа дней в году с температурами ниже нуля при потеплении климата в середине (2041-2050 гг.) и в конце (2091-2100 гг.) 21-го века по
Уменьшение числа дней в году с температурами ниже нуля при потеплении климата в середине (2041-2050 гг.) и в конце (2091-2100 гг.) 21-го века по  Критерии оценивания работ, представляемых на НПК НОУ.
Критерии оценивания работ, представляемых на НПК НОУ. «Об итогах работы с одаренными детьми на муниципальном и региональном уровнях в 2011 году и направлениях работы в 2012 году».
«Об итогах работы с одаренными детьми на муниципальном и региональном уровнях в 2011 году и направлениях работы в 2012 году». Пейзажные зарисовки
Пейзажные зарисовки Герман Степанович Титов
Герман Степанович Титов Связь культурных и духовных образов России
Связь культурных и духовных образов России Город Курск
Город Курск Производственная система
Производственная система Модернизация передающей части радиорелейной станций Р-414 для работы потоком Е2
Модернизация передающей части радиорелейной станций Р-414 для работы потоком Е2 Мы очень любим сочинять, читать, писать-всё изучать!А чтобы грамотными стать, нам надо русский изучать!
Мы очень любим сочинять, читать, писать-всё изучать!А чтобы грамотными стать, нам надо русский изучать! Как снимать успешное социальное кино с нулевым бюджетом?
Как снимать успешное социальное кино с нулевым бюджетом? Презентация на тему Биогеоценоз и биоценоз
Презентация на тему Биогеоценоз и биоценоз  Feel the emotions
Feel the emotions Форматирование текста в текстовом редакторе MS Word.
Форматирование текста в текстовом редакторе MS Word. Архитектура 19 века в России
Архитектура 19 века в России Краткий словарь по экономике по теме: рынок ценных бумаг
Краткий словарь по экономике по теме: рынок ценных бумаг