Теория графов

Теория графов – обширный самостоятельный раздел дискретной математики.
Используется при проектировании компьютерных сетей, трубопроводов, строительстве дорог для минимизации затрат на прокладку коммуникаций.

Граф
это конечное множество вершин V и множество ребер R, соединяющих пары вершин, G=(V,R).
Мощности множеств V и R равны N и M.
Множество ребер может быть пустым.
Примеры вершин – объекты любой природы (населенные пункты, компьютерные сети).
Примеры ребер – дороги, стороны, линии.

Вершины, соединенные ребром, называются смежными. Ребра, имеющие общую вершину, также называются смежными.
Ребро и любая из его двух вершин называются инцидентными.
Степень вершины – количество инцидентных ей ребер.
Каждый граф можно представить на плоскости множеством точек, соответствующих вершинам, которые соединены линиями, соответствующими ребрам.

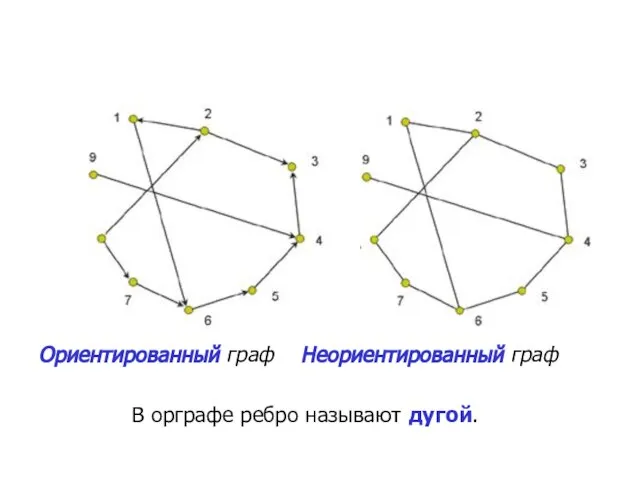
Ориентированный граф Неориентированный граф
В орграфе ребро называют дугой.

Маршрут графа – последовательность вершин и ребер.
Маршрут замкнутый (циклический), если начальная и конечная вершины совпадают.
Маршрут – простая цепь, если все вершины и ребра различны.
Граф связный, если каждая вершина достижима из любой другой.
Вершины, не имеющие инцидентных ребер, называются изолированными.

Взвешенный граф (сеть) – граф, ребрам или дугам которого поставлены в соответствие числа (вес).
Вес сети равен сумме весов ее ребер.

Способы описания графа:
матрица инциденций,
матрица смежности,
списки связи,
перечни ребер.

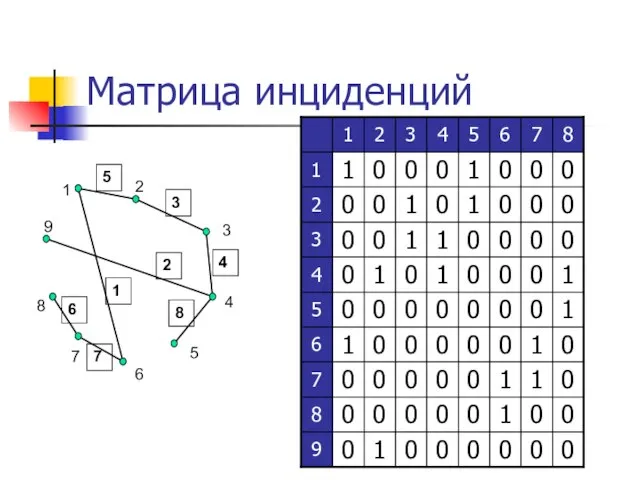
Матрица инциденций
N – количество вершин
M – количество ребер
Матрица инциденций – это двумерный массив размерности N×M

Матрица инциденций
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8

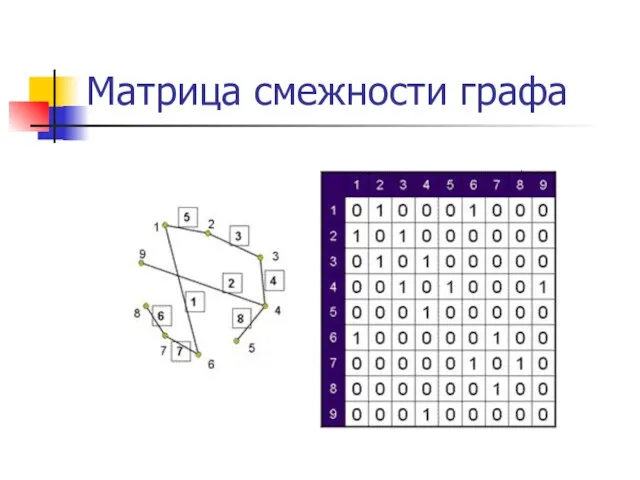
Матрица смежности
– это двумерный массив N*N.

Матрица смежности графа

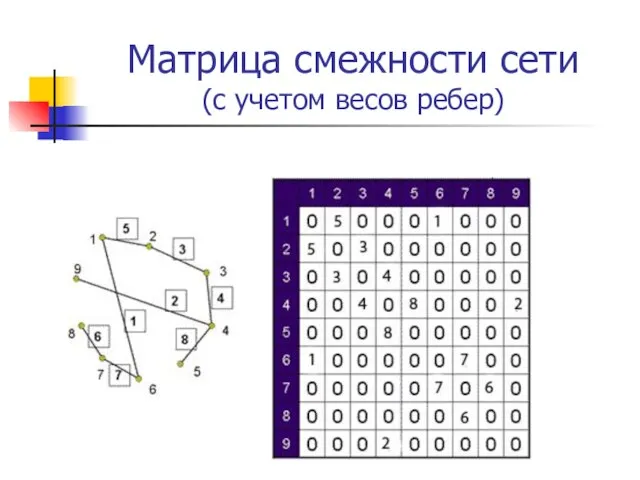
Матрица смежности сети
(с учетом весов ребер)

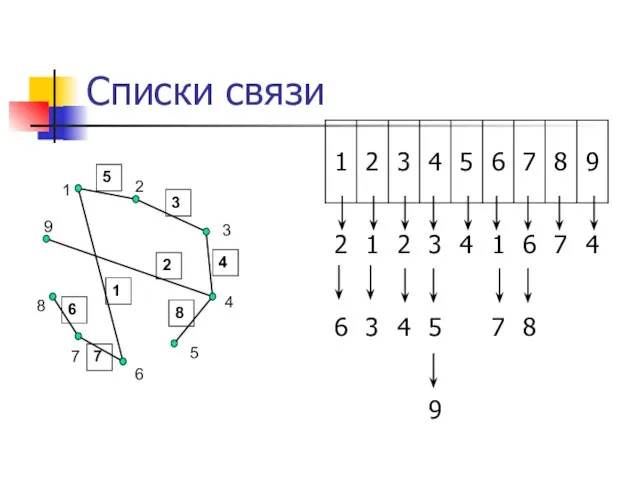
Списки связи
Задание графа списками связи осуществляется с помощью одномерного массива размерности N для хранения указателей.
Элемент массива – указатель на начало списка, в котором содержится информация о вершинах графа, смежных с рассматриваемой.

Списки связи
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8

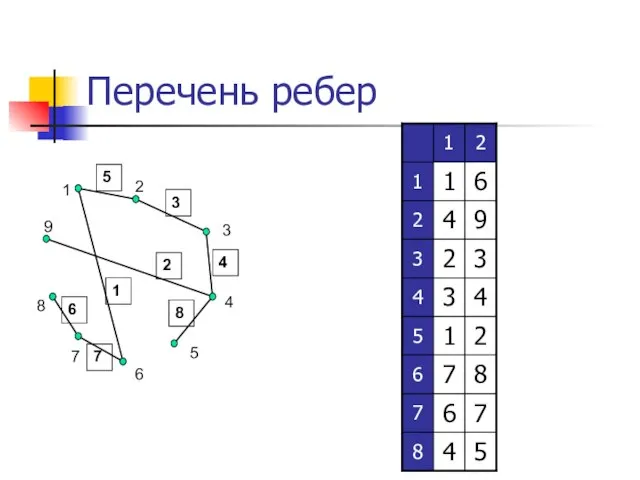
Перечень ребер
Для хранения перечня ребер необходим двумерный массив размерности M×2.
Строка массива описывает ребро.

Перечень ребер
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8

Подграфы и деревья
Подграф графа G называют граф, у которого все вершины и ребра принадлежат графу G.
Остовной связный подграф – это подграф графа G, который содержит все его вершины и каждая его вершина достижима из любой другой.

Подграфы и деревья
Дерево – это граф, в котором нет циклов.
Остовное связное дерево – подграф, включающий все вершины исходного графа G, каждая вершина которого достижима из любой другой, и при этом не содержащий циклов.

Преобразование графа в остовное связное дерево минимального веса
Пусть G=(V,R) – связанный взвешенный неориентированный граф.
Граф G можно представить в виде матрицы смежности, содержащий значения весов ребер.

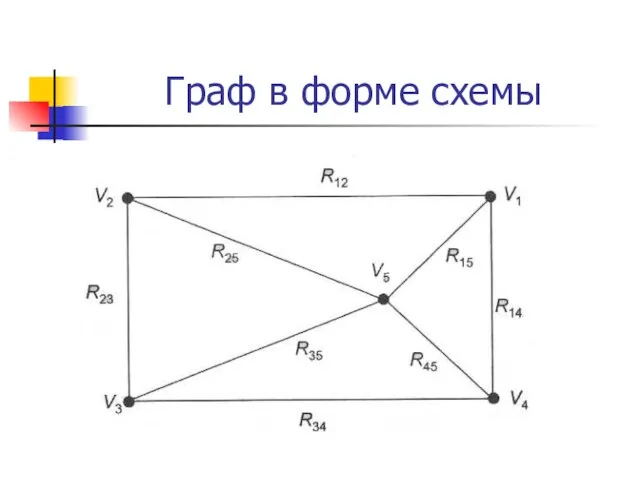
Граф в форме схемы

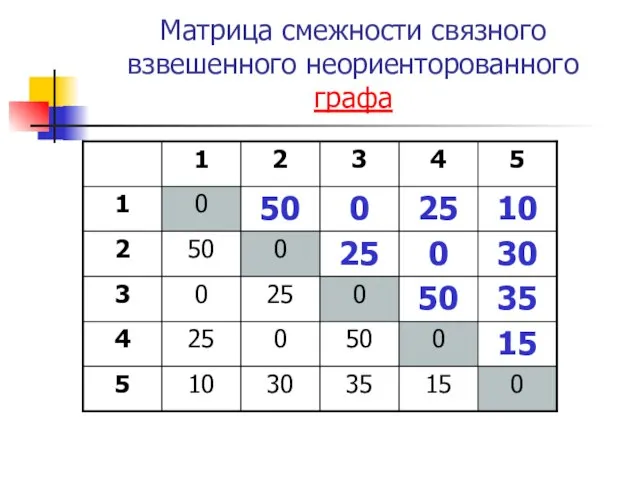
Матрица смежности связного взвешенного неориенторованного графа

Подграф графа, остовной связный подграф, остовное связное дерево

Цикломатическое число γ показывает сколько ребер графа нужно удалить, чтобы в нем не осталось циклов.
γ=m-n+1
Пример, γ=8-5+1=4
Для каждого графа обычно существует несколько связных деревьев, с различными весами.

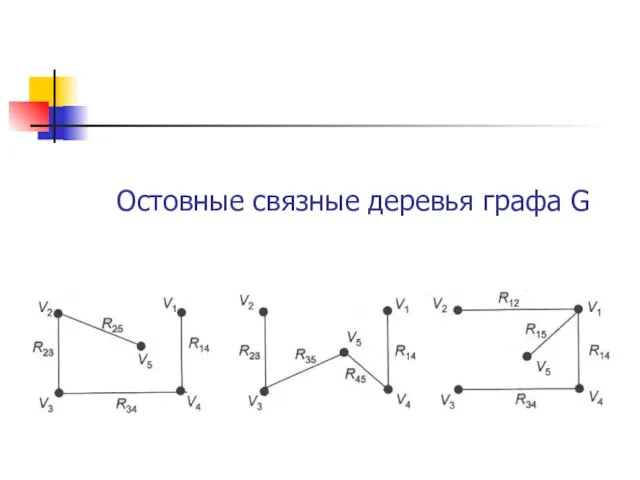
Остовные связные деревья графа G

Построение остовного связного дерева минимального веса.
Алгоритм Крускала
Из графа удаляют все ребра, получается остовной подграф, где все вершины изолированы. Каждая вершина помещается в одноэлементное подмножество.
Ребра сортируются по возрастанию весов.
Ребра последовательно, по возрастанию их весов, включаются в остовное дерево.

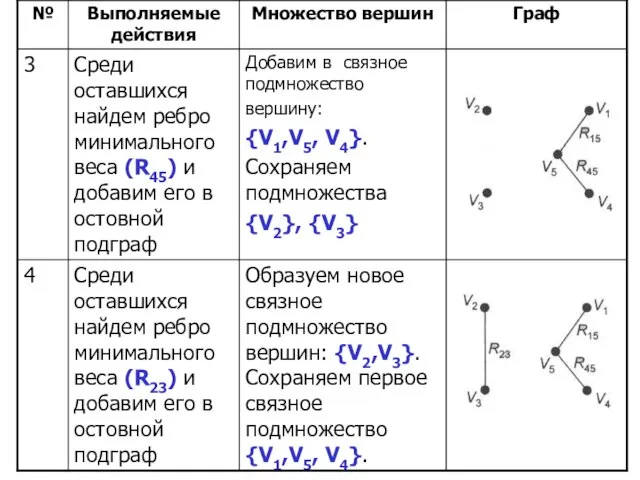
Существует 4 случая:
1) обе вершины включаемого ребра принадлежат одноэлементным подмножествам, тогда они объединяются в новое, связное подмножество;
2) одна из вершин принадлежит связному подмножеству, а другая нет, тогда включаем вторую в подмножество, которому принадлежит первая;
3) обе вершины принадлежат разным связным подмножествам, тогда объединяем подмножества;
4) Обе вершины принадлежат одному связному подмножеству, тогда исключаем данное ребро.

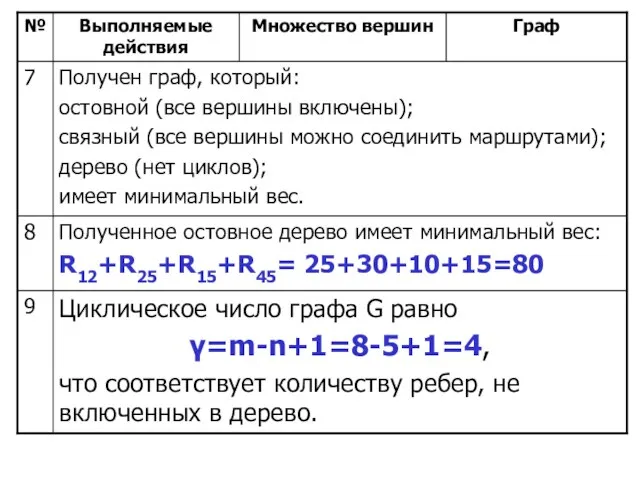
Алгоритм заканчивает работу, когда все вершины будут объединены в одно множество, при этом оставшиеся ребра не включаются в остовное дерево.

Пример построения остовного дерева минимального веса для графа G

Вопросы для закрепления
В какой форме можно представить граф?
В чем разница между орграфом и не орграфом?
Какие графы являются деревьями?
Какой граф обладает минимальным весом?

Изучение графов на языке Паскаль.
Построить остовные связные
деревья минимального веса для графов с 5-ю вершинами
Матрицу смежности графа и дерева вывести в виде таблиц.

Объявление переменных
Два целочисленных пятиэлементных массива X и Y для хранения координат вершин графа
Целочисленный двумерный массив R для хранения весов ребер графа
Целочисленные переменные i, n и k для счетчиков циклов
Целочисленная переменная S для хранения суммы весов ребер дерева минимального веса

Генерация случайных координат 5-ти вершин графа (цикл по i).
Вычисление весов ребер. Вывод матрицы смежности взвешенного орграфа (вложенные циклы по n и по k)
Вывод матрицы смежности взвешенного неориентрованного графа – половины элементов начальной матрицы (начальное значение k=n+1)
Тело программы

Построение остовного связанного дерева минимального веса с учетом 4-х случаев.
Тело программы

Даны координаты вершин графа. Вычислить весы ребер. Вывести матрицу смежности взвешенного неориентированного графа.
Построить остовное связное дерево минимального веса.
V1(50,59)
V2(84,6)
V3(70,32)
V4(22,59)
V5(91,40)

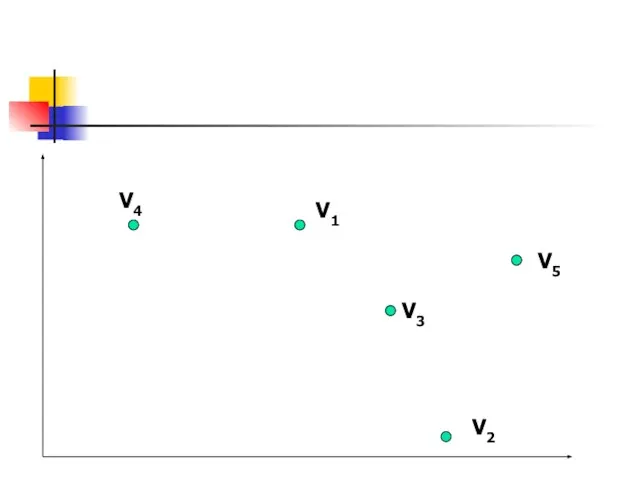
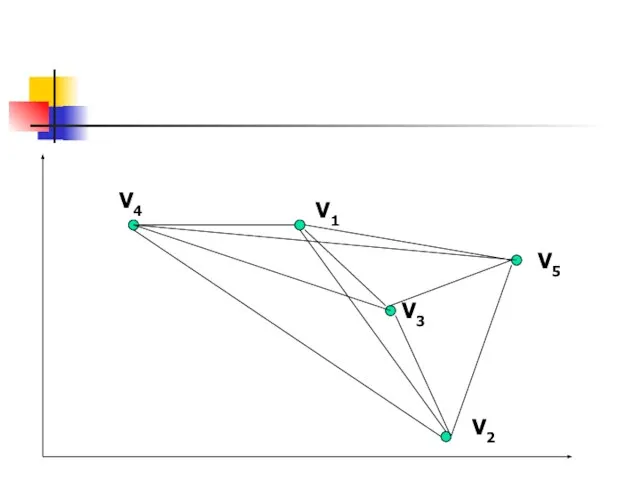
V1
V2
V3
V4
V5

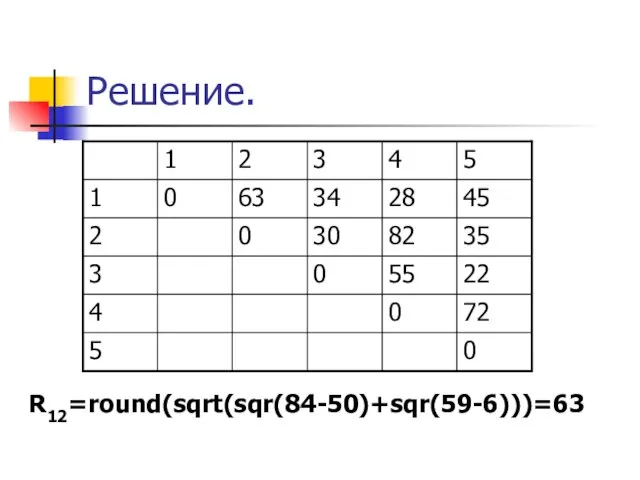
Решение.
R12=round(sqrt(sqr(84-50)+sqr(59-6)))=63

V1
V2
V3
V4
V5

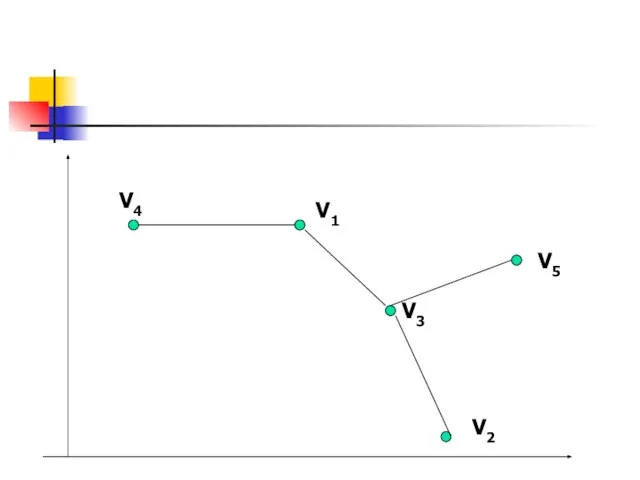
Решение.
мин R35=22, {3,5}
мин R14=28, {3,5}, {1,4}
мин R23=30, {3,5,2}, {1,4}
мин R13=34, {1,2,3,4,5}
S=22+28+30+34=114

V1
V2
V3
V4
V5

Ответы
50 59
84 6
70 32
22 59
91 40
63 34 28 45
30 82 35
55 22
72
22 3 5
28 1 4
30 2 3
34 1 3
114

68 50
22 88
86 10
78 58
79 29
Даны координаты вершин графа.
Вычислить весы ребер. Вывести матрицу смежности взвешенного неориентированного графа. Построить остовное связное дерево минимального веса.

Ответы
68 50
22 88
86 10
78 58
79 29
60 44 13 24
101 64 82
49 20
29
13 1 4
20 3 5
24 1 5
60 1 2
117

Практическая работа
46 51
51 83
43 53
6 60
17 96
32 4 41 54
31 51 36
38 50
38
6
4 1 3
31 2 3
36 2 5
38 3 4
109

4 67
45 74
25 39
43 83
4 33
42 35 42 34
40 9 58
48 22
63
6
9 2 4
22 3 5
34 1 5
35 1 3
100

83 88
78 64
1 43
89 34
83 51
25 94 54 37
80 32 14
88 82
18
6
14 2 5
18 4 5
25 1 2
80 2 3
137

65 34
69 12
33 63
57 18
18 58
22 43 18 53
62 13 69
51 16
56
6
13 2 4
16 3 5
18 1 4
43 1 3
90

29 35
64 37
26 58
73 1
47 82
35 23 56 50
43 37 48
74 32
85
6
23 1 3
32 3 5
35 1 2
37 2 4
127

40 57
7 70
86 76
88 3
98 81
35 50 72 63
79 105 92
73 13
79
6
13 3 5
35 1 2
50 1 3
72 1 4
170

48 37
86 62
40 3
31 40
99 70
45 35 17 61
75 59 15
38 89
74
6
15 2 5
17 1 4
35 1 3
38 3 4
105

2 23
96 36
56 76
89 96
1 20
95 76 114 3
57 60 96
39 78
116
6
3 1 5
39 3 4
57 2 3
60 2 4
159

87 51
11 6
51 15
66 51
59 34
88 51 21 33
41 71 56
39 21
18
6
18 4 5
21 1 4
21 3 5
41 2 3
101