Содержание
- 2. Федеральный государственный образовательный стандарт дошкольного образования от 17 октября 2013 г. N 1155 2.6. Содержание Программы
- 3. Формирование элементарных математических представлений – это целенаправленный процесс передачи и усвоения знаний, приемов и способов умственной
- 4. Задачи формирования элементарных математических знаний и последующего математического развития детей: -приобретение знаний о множестве, числе, величине,
- 5. Современные авторы связывают процесс математического развития ребенка, прежде всего, с развитием его познавательной сферы, разнообразных способов
- 6. Теоретические основы формирования и развития математических представлений у дошкольников Основная цель теоретических основ развития математических представлений
- 7. Основные математические понятия Ключевые слова: множество, число, цифра натуральный ряд чисел, операции с множествами, объединение множеств,
- 8. Множества и операции над ними
- 9. Множество-основное понятие курса математики. Суть понятия передается словами «совокупность», «собрание», «набор» и т.д. Универсальность понятия- под
- 10. Обозначение множеств Множества обозначаются буквами латинского алфавита: А, В, С, …Z. Как называются объекты, из которых
- 11. а ∈ А Объект а принадлежит множеству А Объект а –элемент множества А Множество А содержит
- 12. а ∉ А Объект а не принадлежит множеству А Объект а не является элементом множества А
- 13. Пусть А –множество однозначных чисел Прочтите запись «3 ∈ А» Что можно сказать о числе 3?
- 14. A={а, в, с, d, е} A={а, в, с, d, е …} Чем отличаются данные множества? Конечные
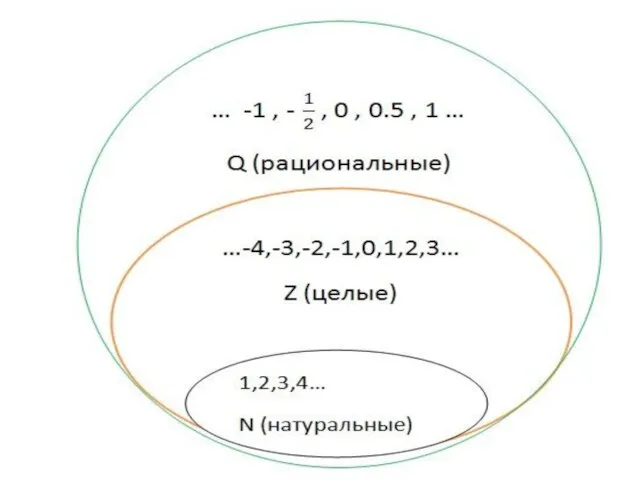
- 15. N-? множество натуральных чисел Натуральные числа-это… Натуральные числа — это числа, используемые для счета предметов или
- 16. Натуральный ряд чисел обладает следующими свойствами: Наименьшим натуральным числом является единица Единица непосредственно не
- 17. Z-? Множество целых чисел Целые числа-это… Натуральные числа, а также все числа противоположные им по знаку,
- 18. Q-? множество рациональных чисел Рациональные числа -это… Рациональные числа - это целые и дробные числа (обыкновенные
- 20. I-? Множество иррациональных чисел Множество иррациональных чисел- это… бесконечные непериодические дроби. √ 3 = 1,730508075... число
- 21. R-? множество действительных чисел Действительное число – это … Действительное число - это любое положительное число,
- 22. Задание №1 выпишите истинные высказывания 1) √4 ∈ N 2) 60/4∈ Z 3) -100 ∈ R
- 23. Способы задания множеств Множество можно задать, перечислив его элементы. А={3, 4, 5, 6 } Такой способ
- 24. Характеристическое свойство элементов Мн-во А – двузначные числа Характеристическое свойство- ? Быть двузначным числом Характеристическое свойство
- 25. Различные характеристические св-ва элементов мн-ва Мн-во В –мн-во квадратов Характеристическое св-ва- ? 1- мн-во прямоугольников с
- 26. Задания № 2 А-множество двузначных чисел, запись которых оканчивается цифрой1. Выпишите числа, которые принадлежат этому множеству
- 27. Отношения между множествами A={а, в, с, d, е} B={ в, d, k, е} в,d,е –общие элементы
- 28. Отношения между множествами A={а, в, с, d, е} B={ с, d, е} Пересекаются, каждый эл-т мн-ва
- 29. Отношения между множествами {∅}-? Приведите пример множества, у которого подмножеством будет {∅} {∅} является подмножеством любого
- 30. Равные множества А=В A= {а, в, с, d, е} В ={а, в, с, d, е} Пересекаются
- 31. Задания № 3. Дано множество Р={3, 5, 7, 9}. Образуй все возможные подмножества множества Р. {3}
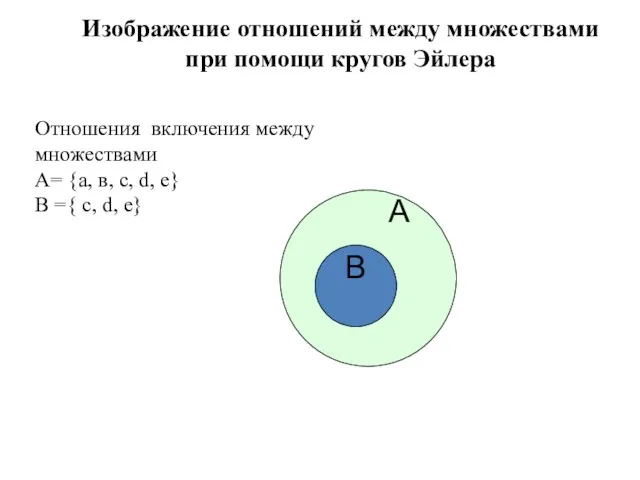
- 32. А Изображение отношений между множествами при помощи кругов Эйлера В Отношения включения между множествами A= {а,
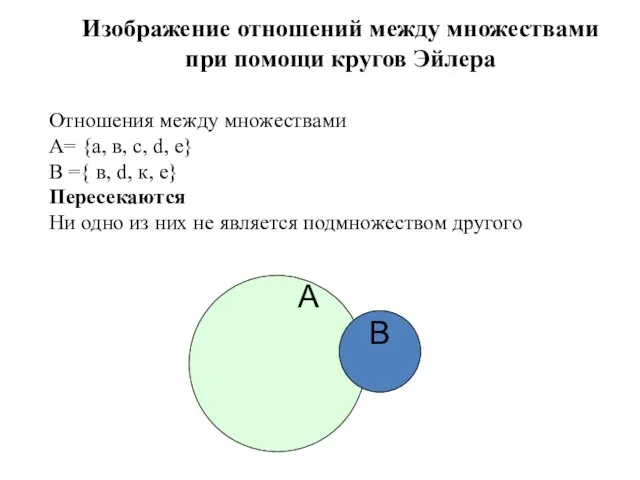
- 33. А Изображение отношений между множествами при помощи кругов Эйлера В Отношения между множествами A= {а, в,
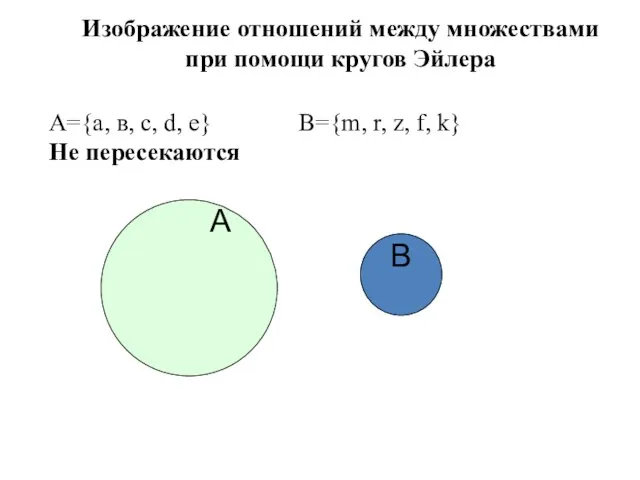
- 34. А Изображение отношений между множествами при помощи кругов Эйлера В A={а, в, с, d, е} В={m,
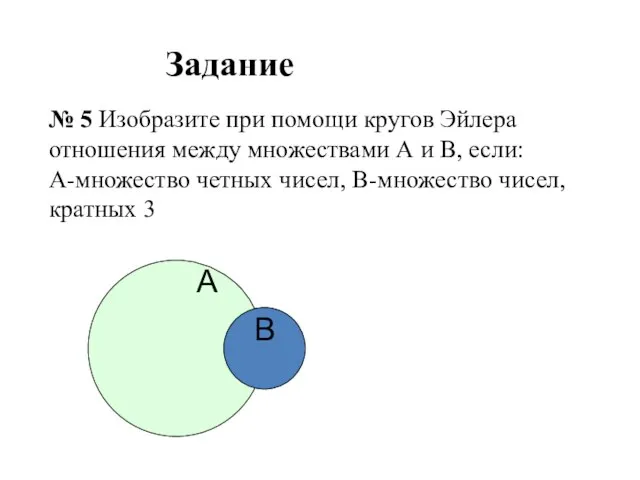
- 35. А В Задание № 5 Изобразите при помощи кругов Эйлера отношения между множествами А и В,
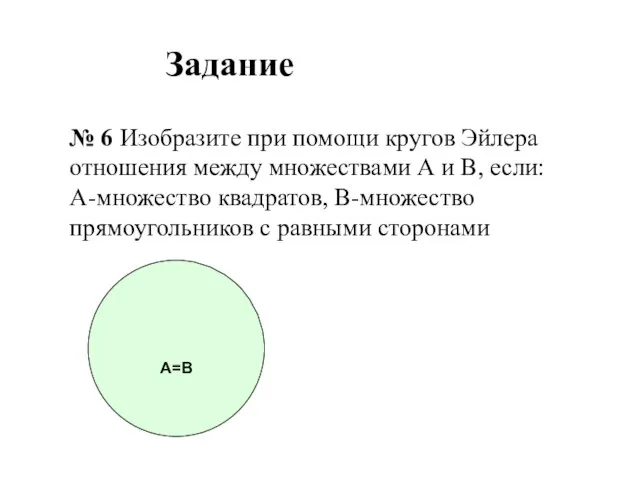
- 36. А=В Задание № 6 Изобразите при помощи кругов Эйлера отношения между множествами А и В, если:
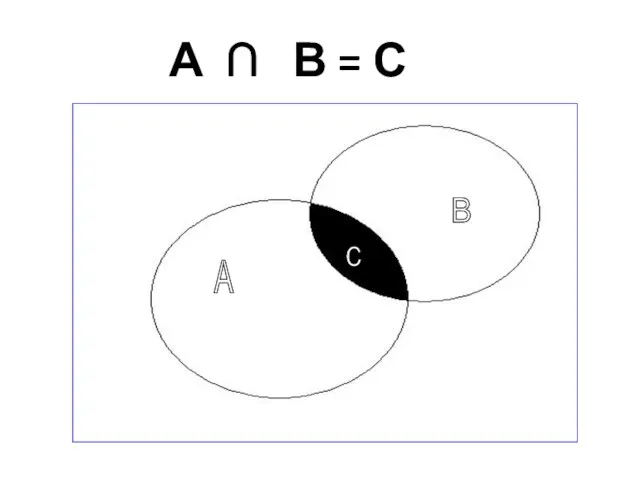
- 37. А ∩ В = С А В с
- 38. Пересечением множеств А и В называется… множество, содержащее только такие элементы, которые принадлежат множеству А и
- 39. А ∩ В = ∅ Множества А и В не имеют общих элементов-пересечение пусто Чтобы найти
- 40. Мн-во А –четные натуральные числа Мн-во В –двузначные натуральные числа Характеристическое св-во эл-тов мн-ва А «быть
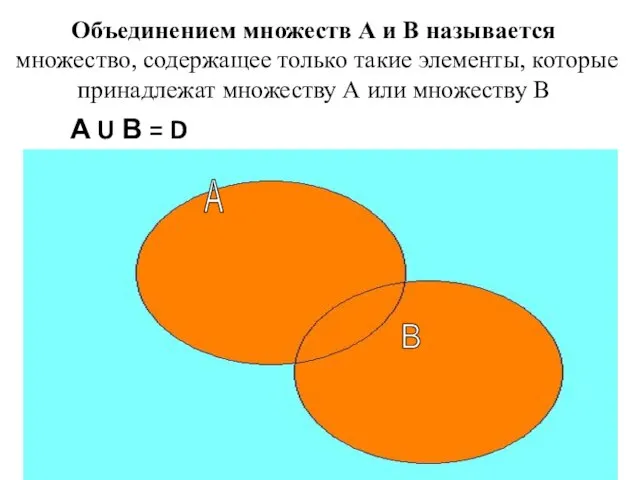
- 41. А U В = D Объединением множеств А и В называется множество, содержащее только такие элементы,
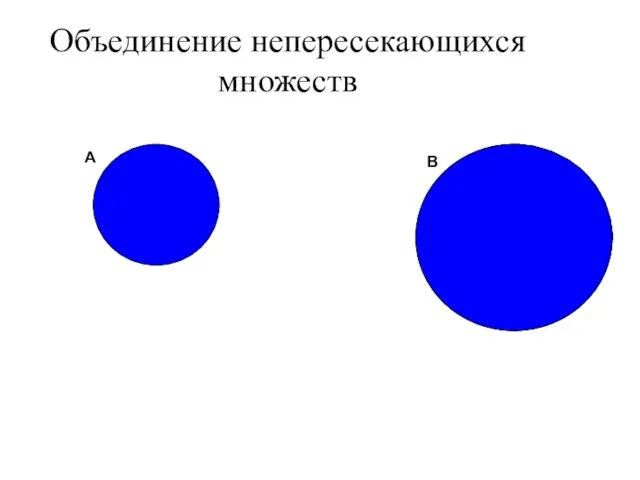
- 42. Объединение непересекающихся множеств В А
- 43. Если эл-ты мн-ва А и В перечислены, то, чтобы найти объединение мн-в А U В достаточно
- 44. Если множества А и В заданы с помощью характеристических св-в, то характеристическое св-во мн-ва А U
- 45. Мн-во А –четные числа Мн-во В –двузначные числа Характеристическое св-во эл-тов мн-ва А «быть четным числом»
- 46. Задание № 7 Мн-во А –четные числа Мн-во В –двузначные числа Выпишите числа, которые принадлежат А
- 47. «ГЕОМЕТРИЯ» «ГЕОГРАФИЯ» Задание № 8 Даны 2 мн-ва букв, из которых составлены слова «геометрия» и «география»
- 48. «ПЕРЕСЕЧЕНИЕ ЭТИХ МНОЖЕСТВ СОСТОИТ ИХ БУКВ: Г Е О Р Ф И Я ОБЪЕДИНЕНИЕ СОСТОИТ ИЗ
- 49. Вместо многоточия поставьте «и» либо «или»: Элемент х принадлежит объединению множеств P и Q тогда и
- 50. Дополнение Пусть В-подмножество А, т.е. В⊂А. Дополнением множества В до множества А называется множество, содержащее только
- 51. Дополнение Если эл-ты мн-ва А и В перечислены, то чтобы найти А\В, достаточно перечислить эл-ты, принадлежащие
- 52. Задание А- множество четных чисел В-множество чисел, кратных 4 Найдите А\В Определите содержатся ли в этом
- 53. Задание № 9 1)Найдите А∪В, А∩В, А\В, В\А, если: А={1,2,4,6} В={6,16,26} А∪В={1,2,4,6,16,26} А∩В={6} А\В={1,2,4} В\А={16,26}
- 54. Классификация-? Это действие распределения объектов по классам на основании сходств объектов внутри класса и их отличия
- 55. Каким условиям должна удовлетворять правильно выполненная классификация? Считают, что множество Х разбито на классы Х1, Х2,…,Хn,если:
- 56. Классификация связана с выделением из множества его подмножеств. Для этого достаточно указать характеристическое св-во его элементов
- 57. Разбиение мн-ва на классы, если указаны 2св-ва(выделение из мн-ва 2 различных подмн-ва) Дано N Выделим 2
- 58. Задания Разбейте множество целых чисел на классы с помощью одного свойства. Установите правильны ли следующие классификации:
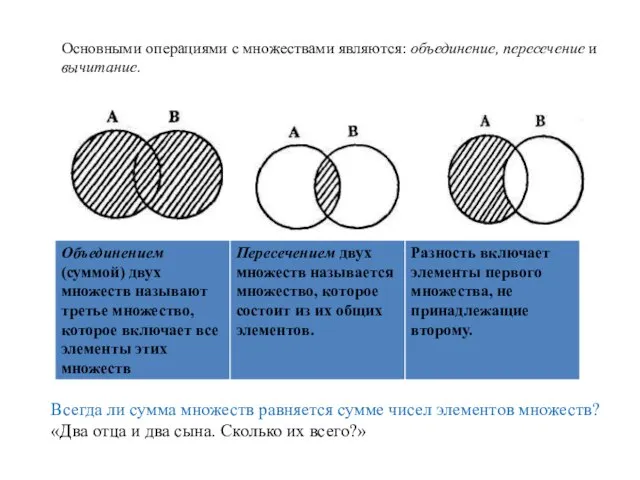
- 59. Основными операциями с множествами являются: объединение, пересечение и вычитание. Всегда ли сумма множеств равняется сумме чисел
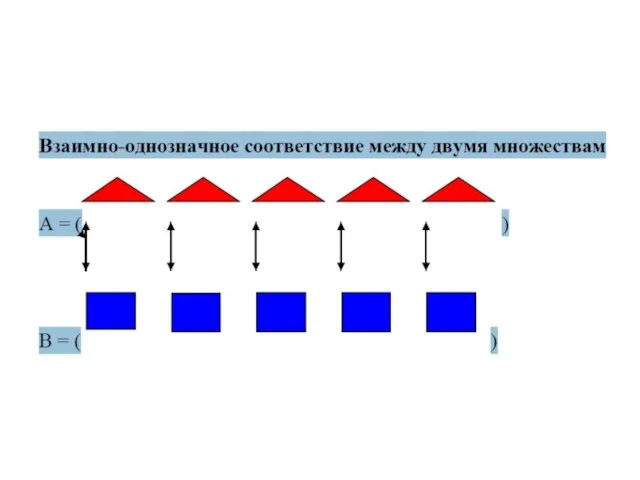
- 61. Счет объектов Счет – это процесс установления взаимно-однозначного соответствия между элементами заданного конечного множества и числами
- 62. Число — показатель мощности прерывной (множества) или непрерывной величины. Число всегда есть отношение этой величины к
- 63. Понятие «величина» в математике рассматривается как основное. Величина — это и протяженность, и объем, и скорость,
- 64. Величина предмета определяется человеком только в сравнении с другой величиной — мерой. Мера является эталоном величины.
- 65. Начальному выделению величины, возникновению элементарных представлений о ней способствуют предметные действия, включающие различные виды непосредственного сопоставления
- 66. Классическая дидактика выделила величину и форму как самостоятельные категории действительности. Уровень познания формы весьма существен, так
- 67. Образцами — эталонами формы выступают геометрические фигуры. Они являются абстрагированием от формы реальных предметов. С помощью
- 68. Основные понятия геометрии Краткая характеристика основных понятий планиметрии Плоские фигуры Краткая характеристика основных понятий стереометрии Объемные
- 71. Основные понятия геометрии Точка — неопределяемое понятие геометрии, элемент пространства. Считается, что точка не имеет ни
- 72. Некоторые характеристические свойства плоскости Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки; Две
- 73. Краткая характеристика основных понятий планиметрии Планиметрия – раздел геометрии, изучающий свойства фигур, лежащих в одной плоскости.
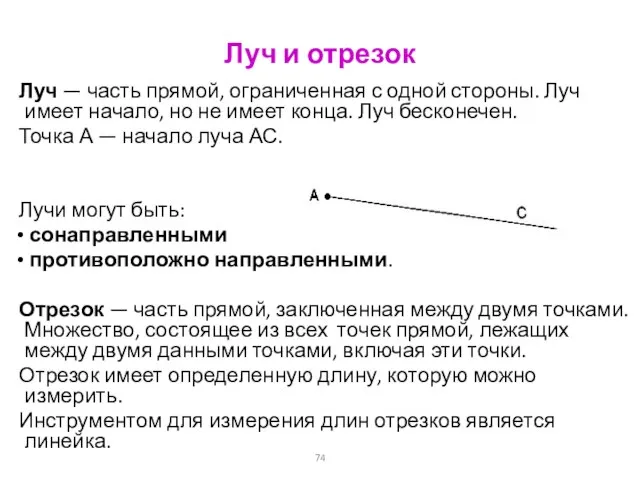
- 74. Луч и отрезок Луч — часть прямой, ограниченная с одной стороны. Луч имеет начало, но не
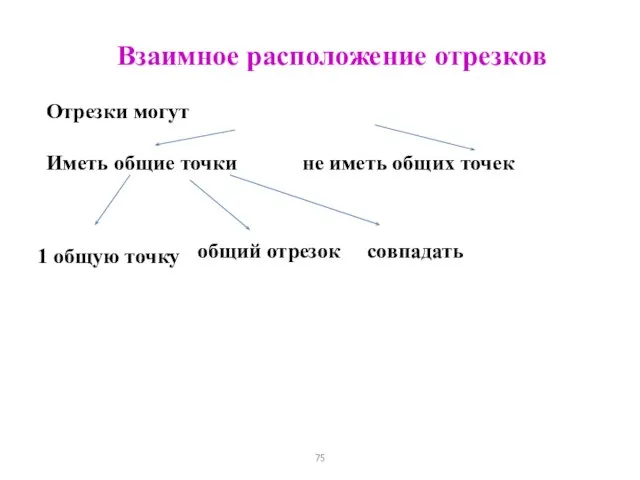
- 75. Взаимное расположение отрезков Отрезки могут Иметь общие точки не иметь общих точек 1 общую точку общий
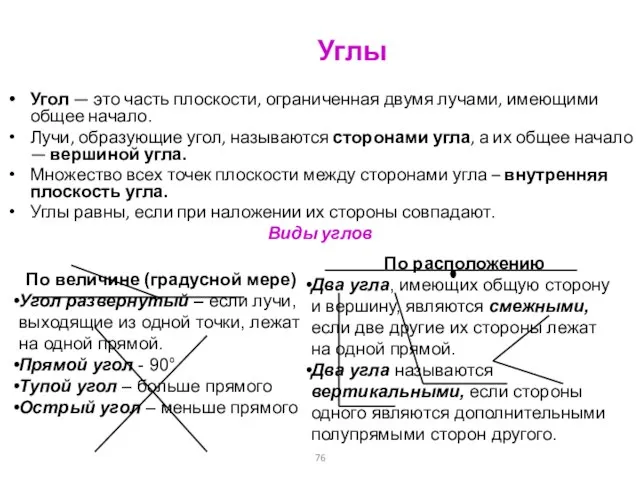
- 76. Углы Угол — это часть плоскости, ограниченная двумя лучами, имеющими общее начало. Лучи, образующие угол, называются
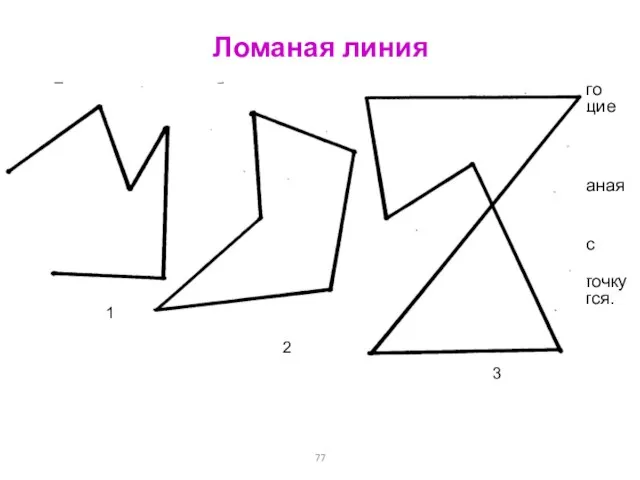
- 77. Ломаная линия Ломаная линия – объединение отрезков, в котором конец каждого отрезка является началом следующего отрезка,
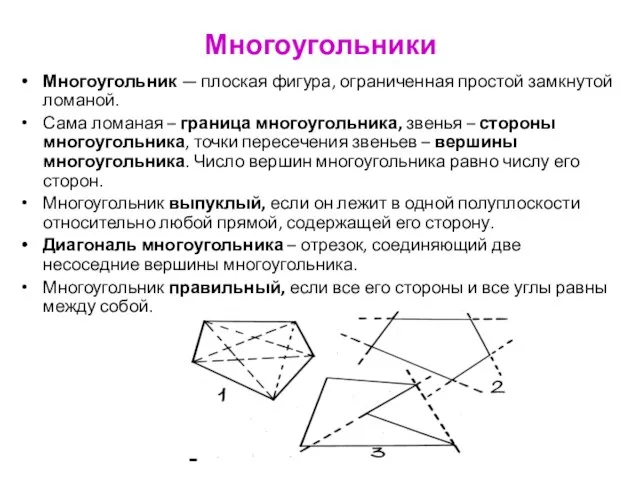
- 78. Многоугольники Многоугольник — плоская фигура, ограниченная простой замкнутой ломаной. Сама ломаная – граница многоугольника, звенья –
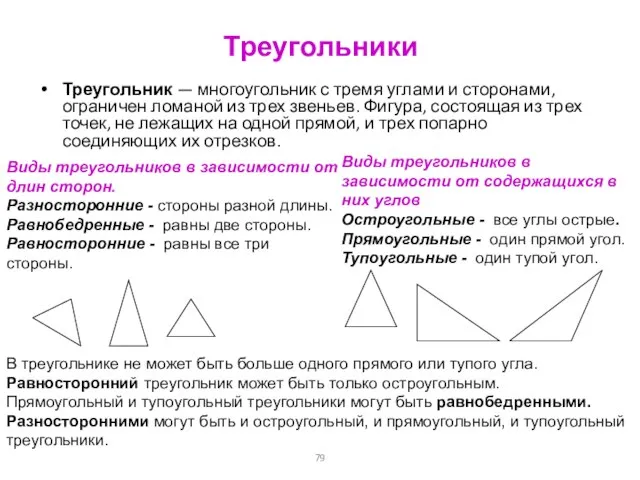
- 79. Треугольники Треугольник — многоугольник с тремя углами и сторонами, ограничен ломаной из трех звеньев. Фигура, состоящая
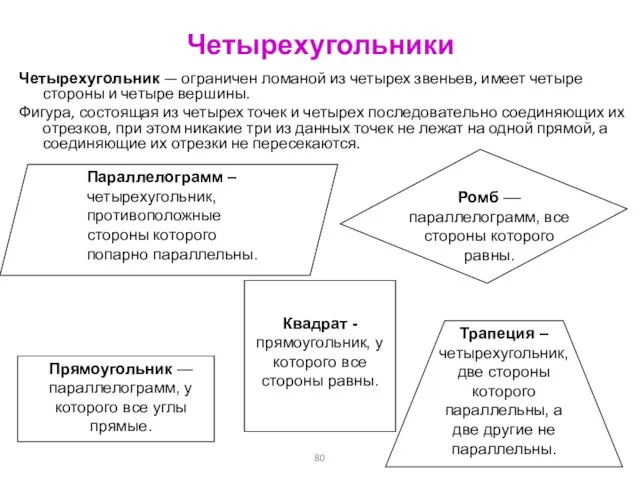
- 80. Четырехугольники Четырехугольник — ограничен ломаной из четырех звеньев, имеет четыре стороны и четыре вершины. Фигура, состоящая
- 81. Среди следующих предложений укажите истинные, ответы обоснуйте: Если в четырехугольнике все углы прямые, то этот четырехугольник
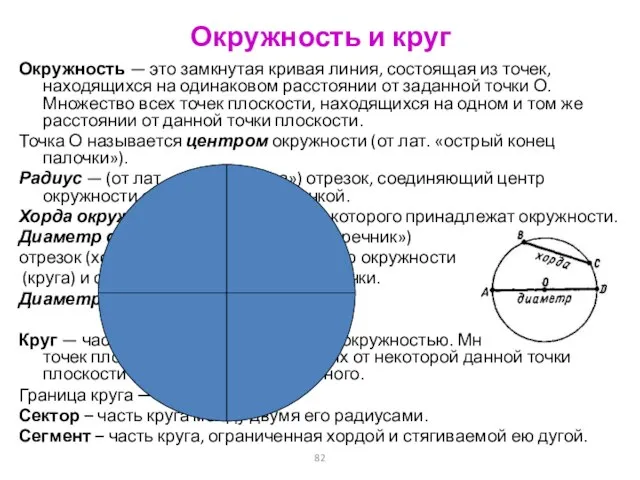
- 82. Окружность и круг Окружность — это замкнутая кривая линия, состоящая из точек, находящихся на одинаковом расстоянии
- 83. Краткая характеристика основных понятий стереометрии Стереометрия – раздел геометрии, который изучает свойства всех фигур пространства. Объемные
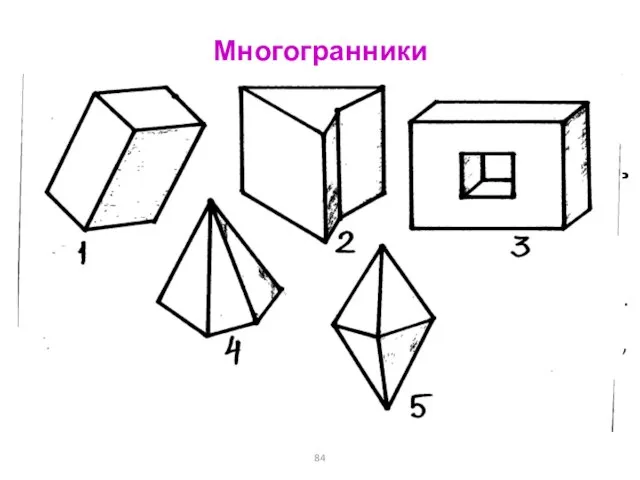
- 84. Многогранники Многогранник – тело, поверхность которого состоит из конечного числа плоских многоугольников. Грани многогранника – плоские
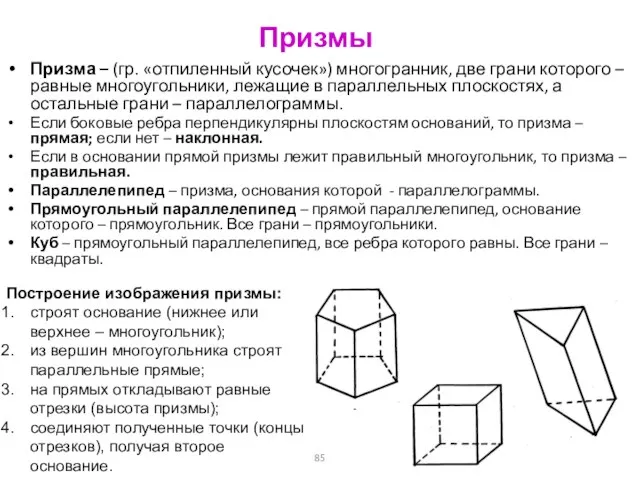
- 85. Призмы Призма – (гр. «отпиленный кусочек») многогранник, две грани которого – равные многоугольники, лежащие в параллельных
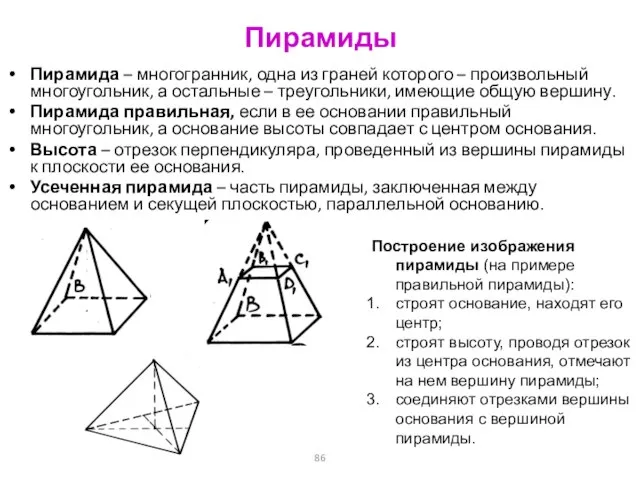
- 86. Пирамиды Пирамида – многогранник, одна из граней которого – произвольный многоугольник, а остальные – треугольники, имеющие
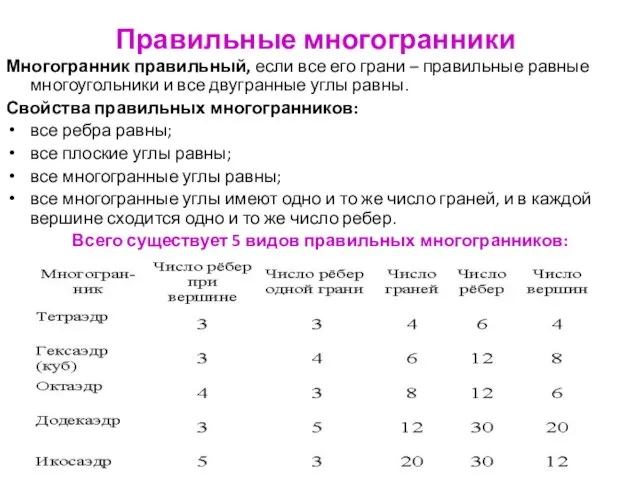
- 87. Правильные многогранники Многогранник правильный, если все его грани – правильные равные многоугольники и все двугранные углы
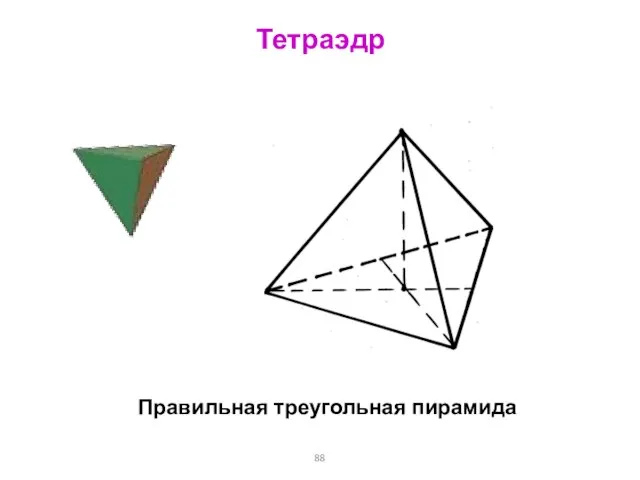
- 88. Тетраэдр Правильная треугольная пирамида
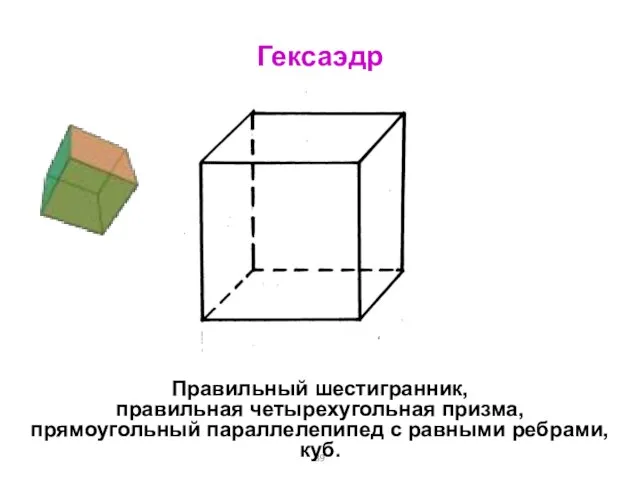
- 89. Гексаэдр Правильный шестигранник, правильная четырехугольная призма, прямоугольный параллелепипед с равными ребрами, куб.
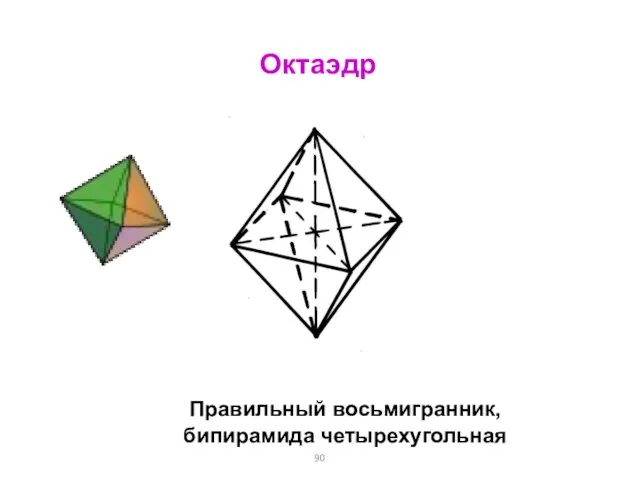
- 90. Октаэдр Правильный восьмигранник, бипирамида четырехугольная
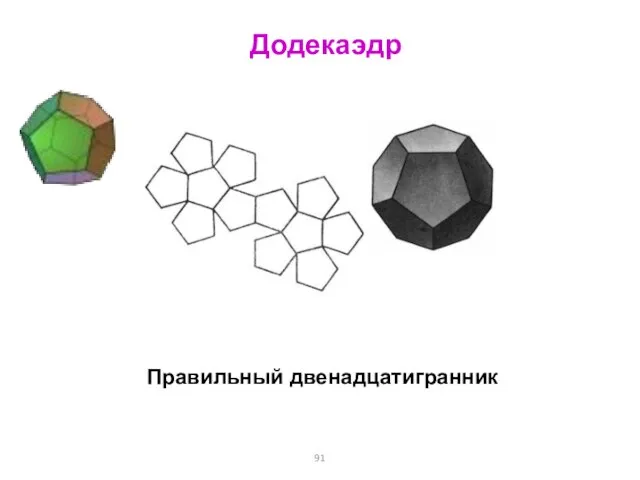
- 91. Додекаэдр Правильный двенадцатигранник
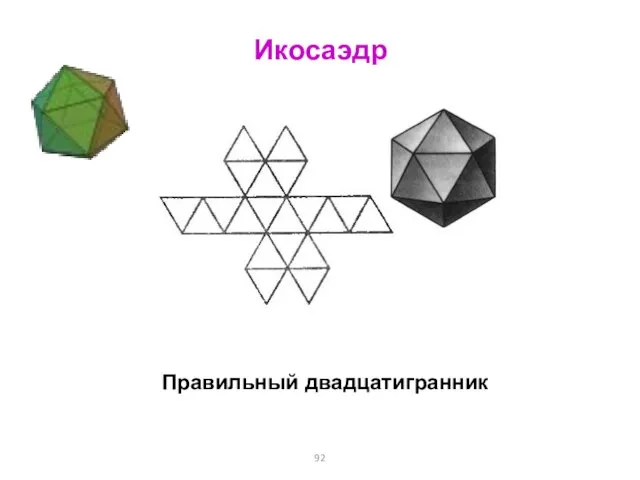
- 92. Икосаэдр Правильный двадцатигранник
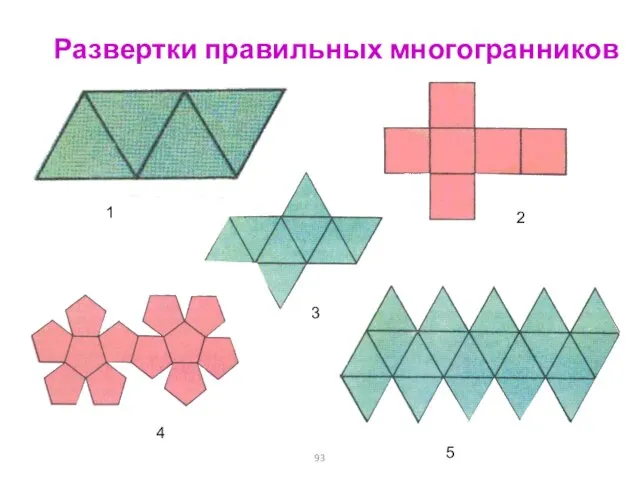
- 93. Развертки правильных многогранников 1 2 3 4 5
- 94. Тела вращения Тела вращения образуются при вращении плоской фигуры вокруг не пересекающей ее оси, имеют гладкие
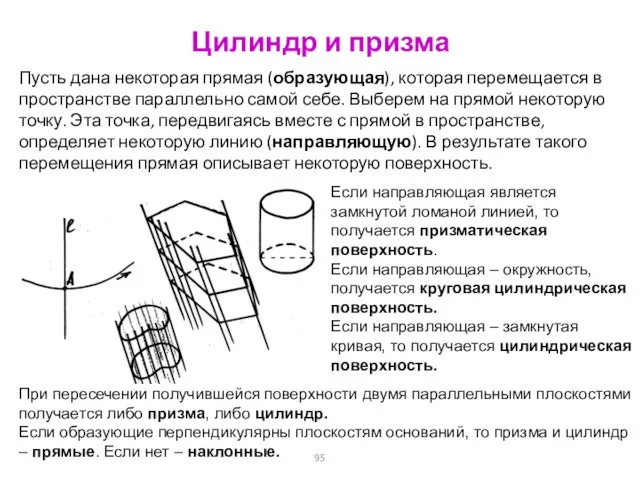
- 95. Цилиндр и призма Пусть дана некоторая прямая (образующая), которая перемещается в пространстве параллельно самой себе. Выберем
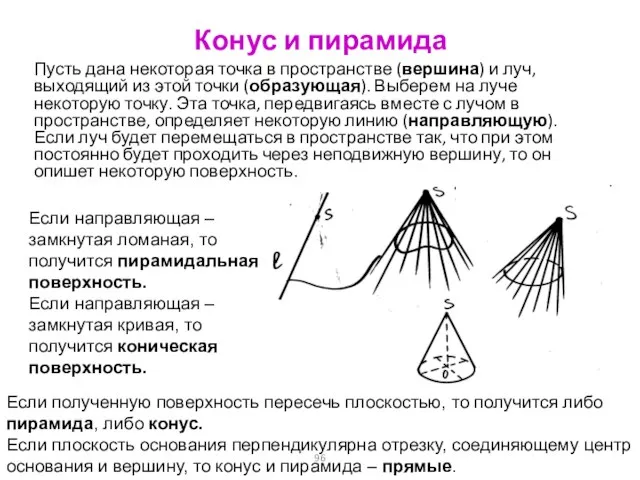
- 96. Конус и пирамида Пусть дана некоторая точка в пространстве (вершина) и луч, выходящий из этой точки
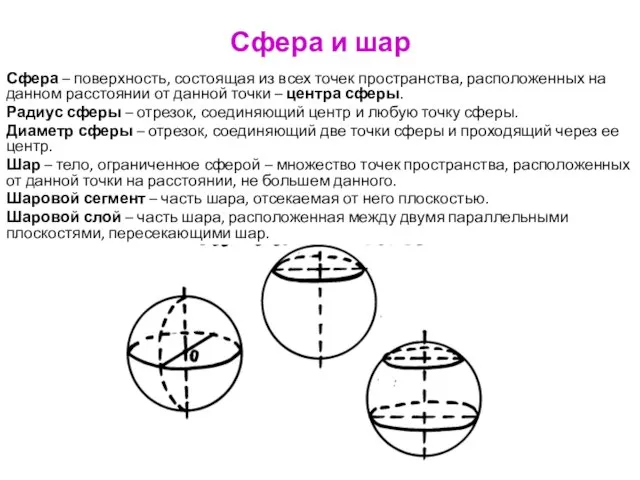
- 97. Сфера и шар Сфера – поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от
- 98. Выбери правильный ответ 1. Конус и цилиндр – это 2. Конус получается вращением а) плоские фигуры
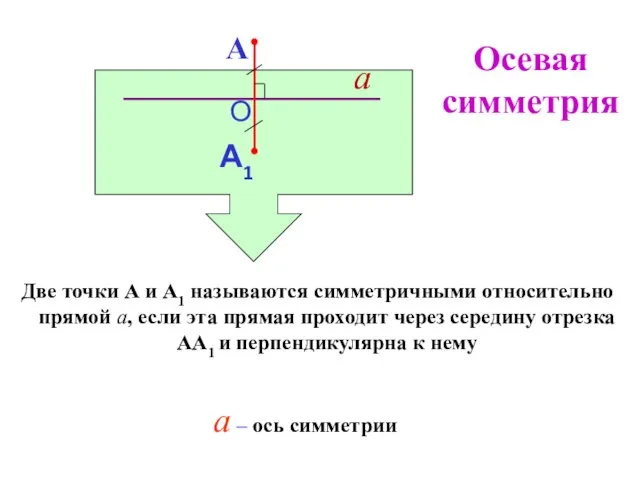
- 99. Понятие симметрии «Симметрия» в переводе с греческого означает «соразмерность» (повторяемость). Симметричным наз. объект, который можно как-то
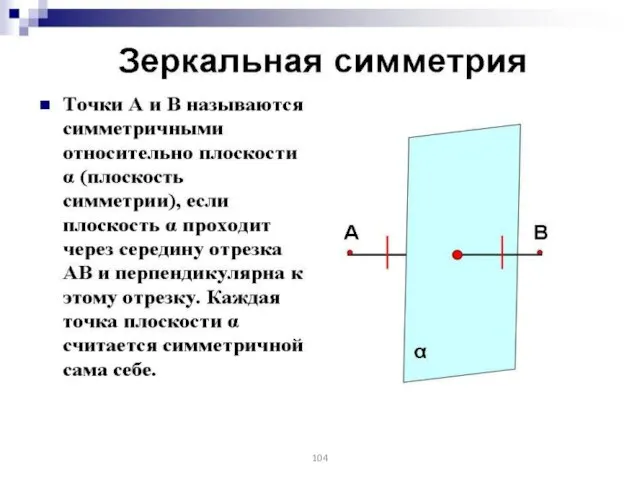
- 100. Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину
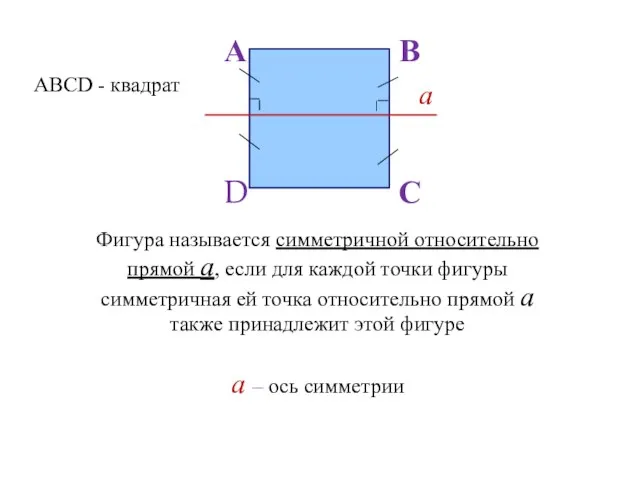
- 101. Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой
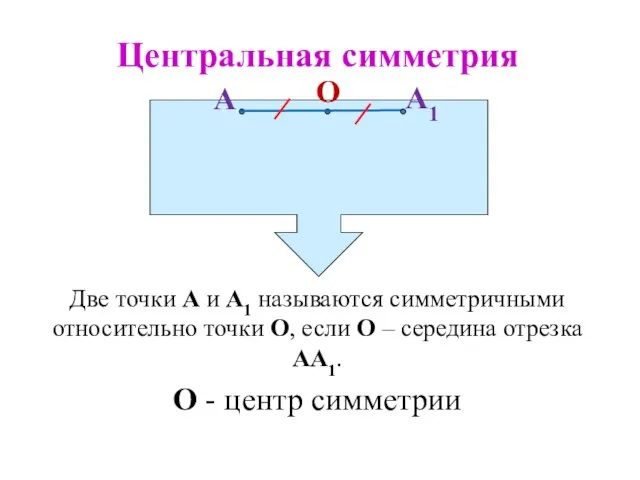
- 102. Две точки А и А1 называются симметричными относительно точки О, если О – середина отрезка АА1.
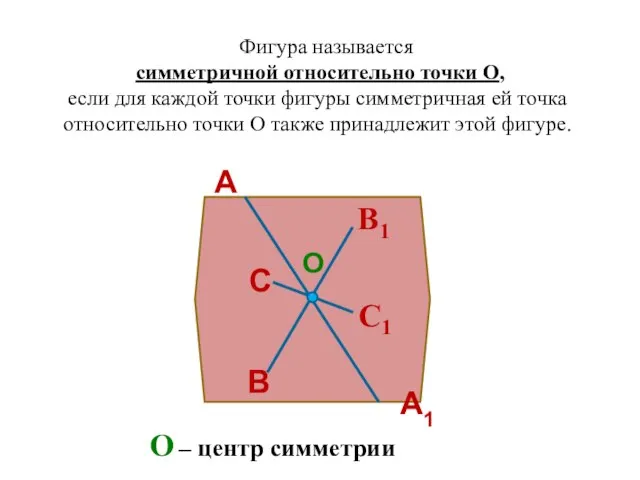
- 103. Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки
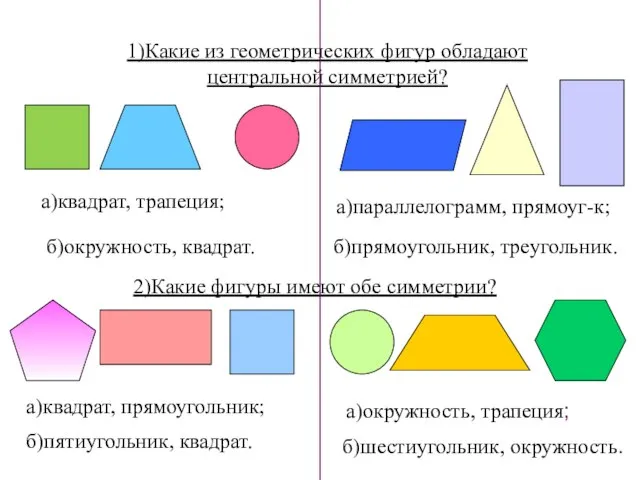
- 106. 1)Какие из геометрических фигур обладают центральной симметрией? 2)Какие фигуры имеют обе симметрии? а)квадрат, трапеция; б)окружность, квадрат.
- 107. В презентации использованы материалы Габовой Марины Анатольевны канд. пед. наук, доцент кафедры ПМДО КГПИ
- 108. Технология математического образования -последовательную систему действий педагога по планированию, применению и оцениванию всего процесса взаимодействия с
- 109. Содержание математического развития дошкольников Под содержанием обучения понимается объем и характер знаний, умений и навыков, которыми
- 110. Основные представления и понятия: «количество», «число», «множество», «подмножество», «величина», «мера», «форма предмета». «геометрические фигуры»; представления о
- 111. Математические зависимости и отношения: отношения между предметными множествами (равночисленность – неравночисленность), отношение порядка в натуральном ряду,
- 112. В методике выделяются две группы математических действий: -основные ( счет, измерение, вычисления); -дополнительные, пропедевтические, сконструированные в
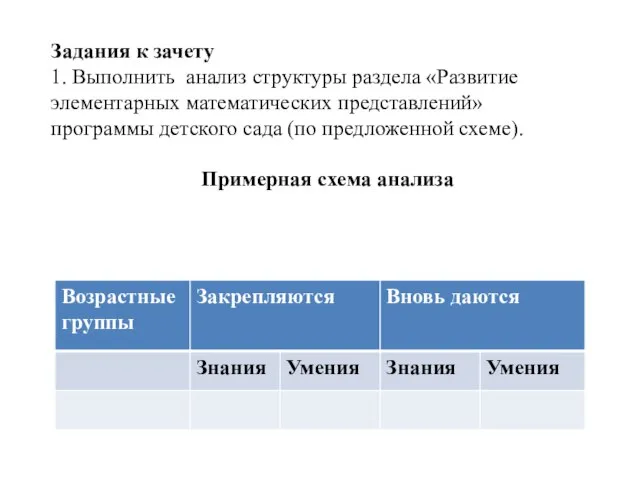
- 113. Задания к зачету 1. Выполнить анализ структуры раздела «Развитие элементарных математических представлений» программы детского сада (по
- 114. 2. Составить библиографический список статей из научно-методических журналов и пособий (не менее 10 наименований) по математическому
- 115. Развитие у детей представлений о множестве Ключевые слова: восприятие и отображение множеств детьми раннего и дошкольного
- 116. Исследования А. М. Леушиной показали, что сначала учить детей надо не числу, а сравнению (способствовать формированию
- 117. Например, игры с куклами. Взрослый просит ребят собрать всех кукол вместе, затем отобрать самых маленьких из
- 118. Развитие у детей представлений о множестве
- 119. Организуя обучение детей, следует: -приучать дошкольников наблюдать за действиями взрослых с предметами, слушать, как словами характеризуются
- 120. Воспитатель должен иметь в виду, что простейшее представление о количестве можно дать детям лишь в том
- 121. К 3 годам активный словарь ребенка включает более чем 1300—1400 слов. Как правило, называют слова-числительные в
- 122. Ребенок становится свидетелем того, как взрослые считают разные предметы: «Принеси две конфеты», «Дай второй ботинок». Это
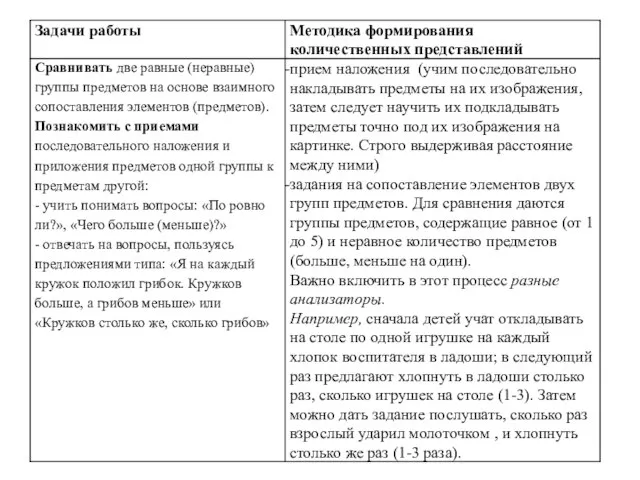
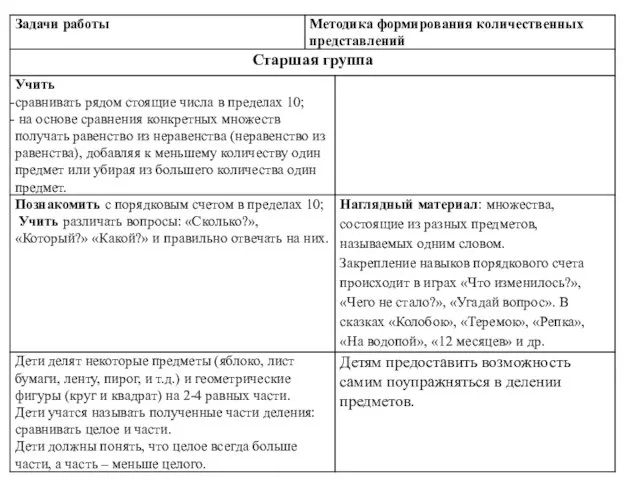
- 123. Этапы формирования количественных представлений. Дочисловой этап и обучение счету
- 129. После усвоения счета предметов дети считают другие объекты: Счет звуков. Дети считают до 5 звуков. Рекомендуется
- 130. Независимость числа от формы расположения предметов и расстояния между предметами. После обучения счету детей знакомят с
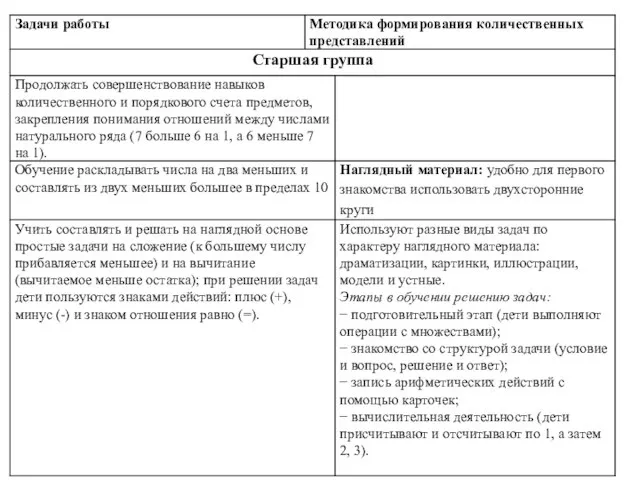
- 135. Методика формирования умения решать и составлять арифметические задачи Арифметические задачи (решаются арифметическим действием). Текстовые задачи (сформулированы
- 136. Методика формирования умения решать и составлять арифметические задачи По характеру наглядности задачи делятся на: 1. Задачи-драматизации
- 137. Методика формирования умения решать и составлять арифметические задачи При обучении дошкольников часто используются различные задачи, отражающие
- 138. Методика формирования умения решать и составлять арифметические задачи Этапы обучения: Подготовительный этап: Работа с множествами, их
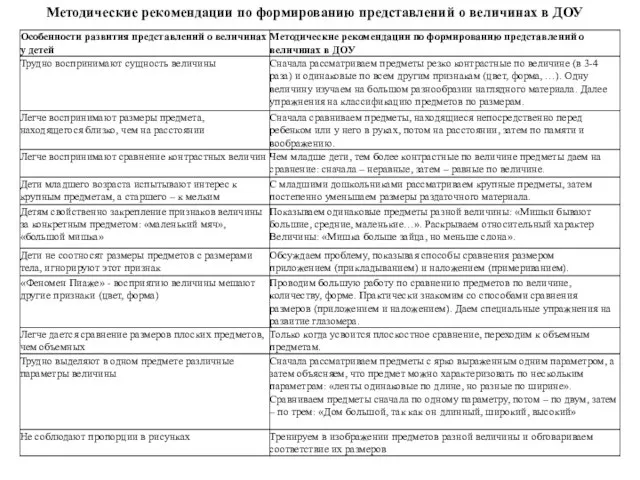
- 139. Особенности и методика формирования и развития у дошкольников представлений о размерах предметов Величина — это и
- 140. Величины, с которыми знакомятся дошкольники Длина – это характеристика линейных размеров предметов. Длины любых предметов можно
- 141. Методические рекомендации по формированию представлений о величинах в ДОУ
- 142. Дошкольники знакомятся: • с плоскими геометрическими фигурами: точкой, различными линиями (обычно в процессе изобразительной деятельности), квадратом,
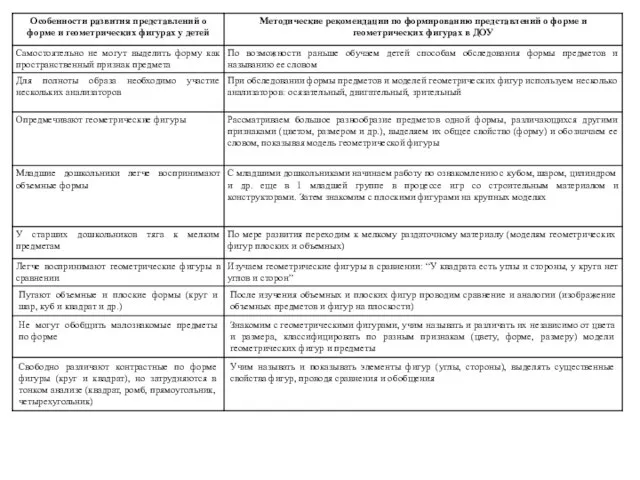
- 143. Особенности формирования и развития у дошкольников представлений о форме предметов и геометрических фигурах Механизмы восприятия формы:
- 144. Особенности формирования и развития у дошкольников представлений о форме предметов и геометрических фигурах Этапы восприятия формы:
- 145. Особенности формирования и развития у дошкольников представлений о форме предметов и геометрических фигурах Этапы восприятия геометрических
- 146. Особенности формирования и развития у дошкольников представлений о форме предметов и геометрических фигурах Этапы восприятия свойств
- 147. Особенности формирования и развития у дошкольников представлений о форме предметов и геометрических фигурах Последовательность в формировании
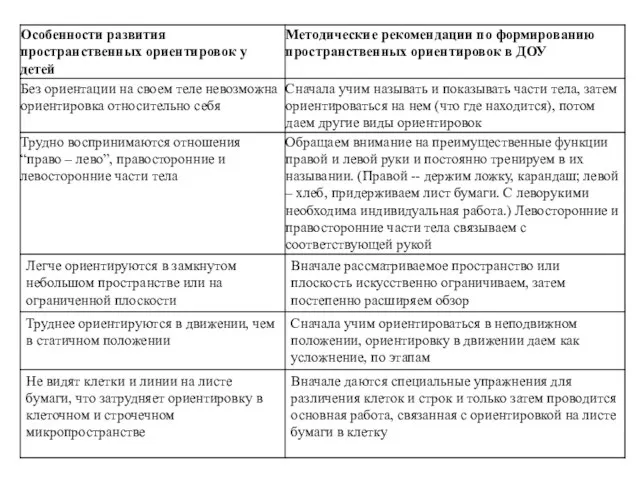
- 149. Особенности и методика формирования и развития пространственных представлений у дошкольников В понятие пространственной ориентации входит оценка
- 150. Особенности и методика формирования и развития пространственных представлений у дошкольников В период раннего детства ребенок ориентируется
- 151. Особенности и методика формирования и развития пространственных представлений у дошкольников Этапы восприятия пространственных отношений между предметами:
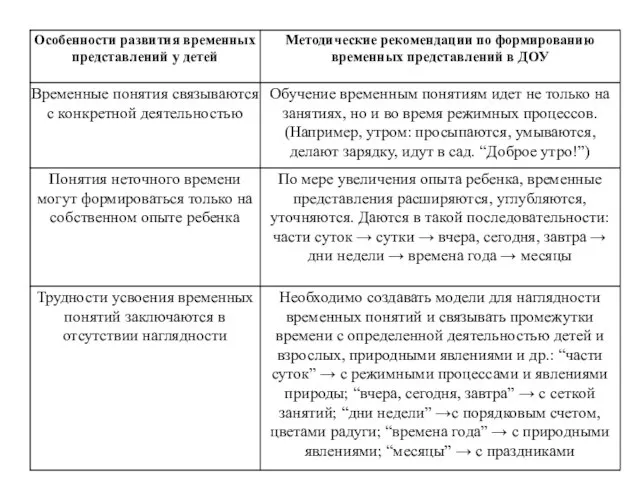
- 153. Особенности и методика формирования и развития представлений о времени у дошкольников Слово «время» происходит от древнерусского
- 154. Особенности и методика формирования и развития представлений о времени у дошкольников Факторы, формирующие чувство времени: -
- 155. Особенности и методика формирования и развития представлений о времени у дошкольников В младшей группе дети способны
- 156. Особенности и методика формирования и развития представлений о времени у дошкольников Значение развития временных представлений у
- 157. Особенности и методика формирования и развития представлений о времени у дошкольников Н.И. Красногорский подчеркивал необходимость развития
- 159. Предметно-развивающая среда как условие эффективного математического развития ребенка. Под развивающей предметно-пространственной средой следует понимать естественную комфортабельную
- 160. Требования к наглядному материалу : -предметы для счета и их изображения должны быть известны детям, они
- 161. Для каждой возрастной группы имеется свой комплект наглядного материала. Это —комплексное дидактическое средство, обеспечивающее формирование элементарных
- 162. Мария Фидлер Математика уже в детском саду : Пособие для воспитателя дет. сада ; Перевод с
- 163. Примеры, рассмотренные в книге, подтверждают возможность проведения самой разнообразной работы как с младшими детьми (трех и
- 164. ДЕТИ МЛАДШЕГО ВОЗРАСТА — ТРЕХ - И ЧЕТЫРЕХЛЕТНИЕ КЛАССИФИКАЦИЯ ПРЕДМЕТОВ ПО РАЗЛИЧНЫМ ПРИЗНАКАМ («принадлежит к...» или
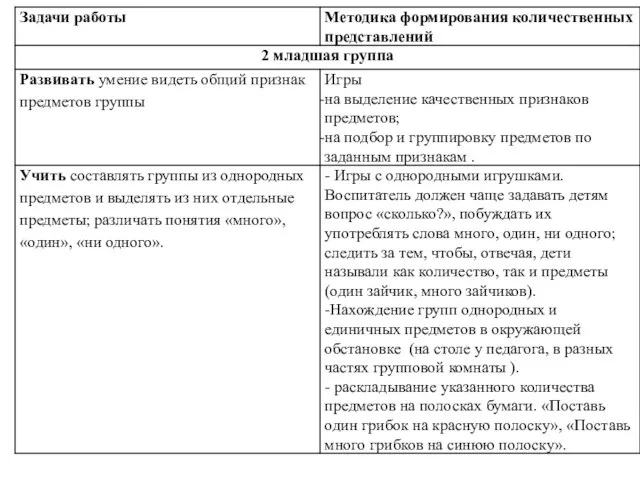
- 165. Дидактический материал по формированию элементарных математических представлений для детей 3–4 лет «Собери неваляшку» Есть у нас
- 166. Этот дидактический материал приготовлен из картона (для более практичности можно заламинировать, с помощью которого решаются сразу
- 167. Задание: Собрать из предложенных фигур неваляшку Какой формы фигуры, из которых собрали неваляшку? Сколько кругов? Какого
- 168. Задание: Под каждый большой круг приложите маленький. Каких кругов больше? Сколько всего будет кругов, если убрать
- 169. "Счетные палочки Кюизенера» Что представляют собой палочки Кюизенера? Каждая палочка Кюизенера символизирует число от 1 до
- 170. Занятия начинаются с простых и понятных малышу игр (подбираем детали по длине и цвету, складываем пирамидку
- 171. Логические блоки Дьенеша Логические блоки придумал венгерский математик и психолог Золтан Дьенеш. Игры с блоками доступно,
- 172. Первое знакомство с геометрическими фигурами Дьенеша Воспитательница сказала детям, что принесла новые кубики, каких у них
- 173. Каждая пара распределяет свои геометрические фигуры так, чтобы было видно, что одни из них — большие,
- 175. В следующий раз игра проводилась по-другому: ребенок, видя перед собой какую-либо геометрическую фигуру, должен был перечислить
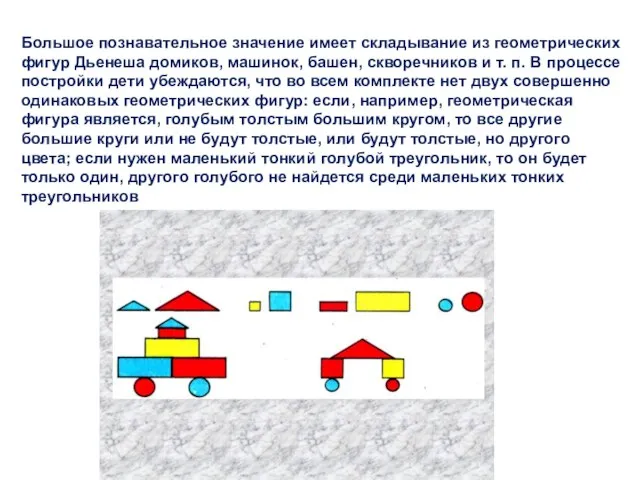
- 176. Большое познавательное значение имеет складывание из геометрических фигур Дьенеша домиков, машинок, башен, скворечников и т. п.
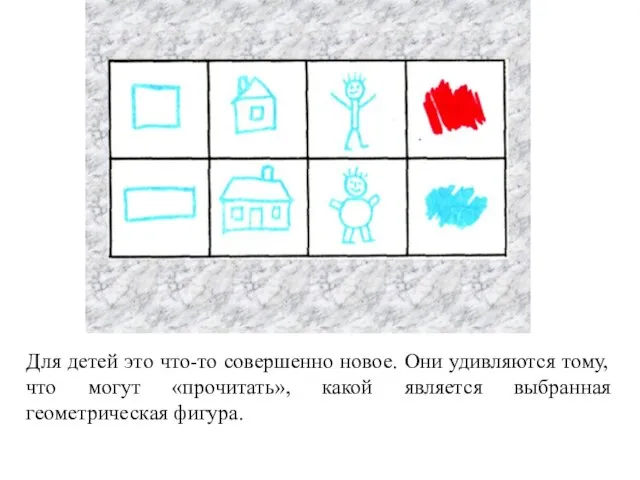
- 177. Для проверки того, насколько хорошо дети усвоили признаки геометрических фигур, был введен специальный код, графически изображающий
- 178. Для детей это что-то совершенно новое. Они удивляются тому, что могут «прочитать», какой является выбранная геометрическая
- 179. Что умеют счетные палочки? 1)Задачи на построение простых фигур; 2)Задачи на построение сложных фигур; 3)Задачи на
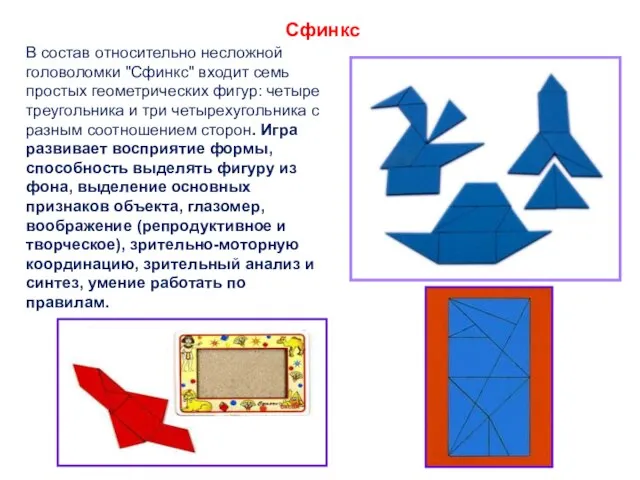
- 180. Сфинкс В состав относительно несложной головоломки "Сфинкс" входит семь простых геометрических фигур: четыре треугольника и три
- 181. Танграм Одна из первых древних игр головоломок. Родина возникновения - Китай, возраст - более 4 000
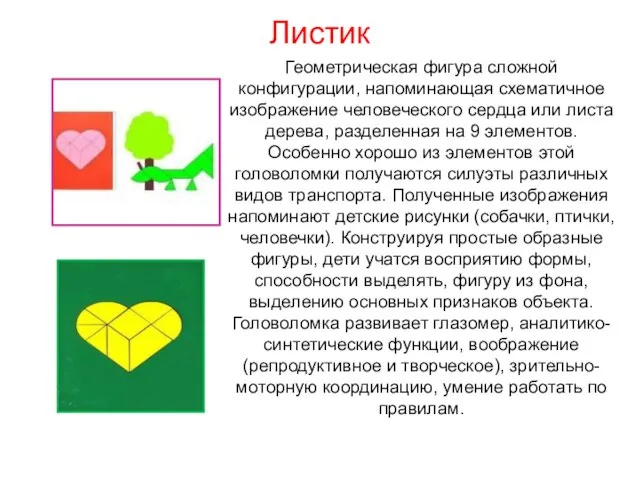
- 182. Листик Геометрическая фигура сложной конфигурации, напоминающая схематичное изображение человеческого сердца или листа дерева, разделенная на 9
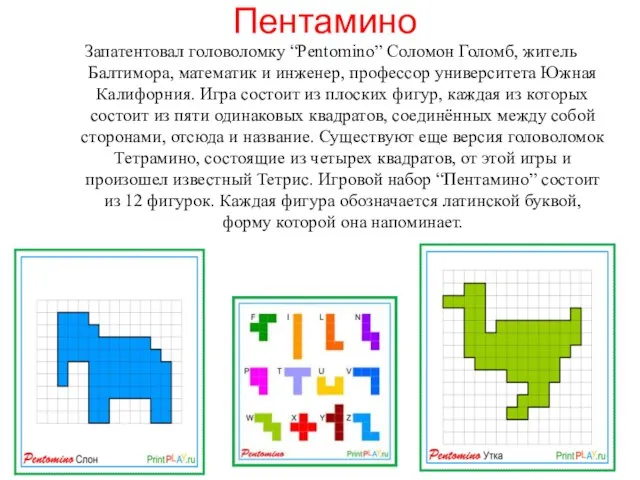
- 183. Пентамино Запатентовал головоломку “Pentomino” Соломон Голомб, житель Балтимора, математик и инженер, профессор университета Южная Калифорния. Игра
- 184. Материалы Монтессори
- 185. ПЕДАГОГИЧЕСКАЯ ДИАГНОСТИКА Педагогическая диагностика позволяет: – установить уровень овладения учебной деятельностью; – выявить характер трудностей ученика
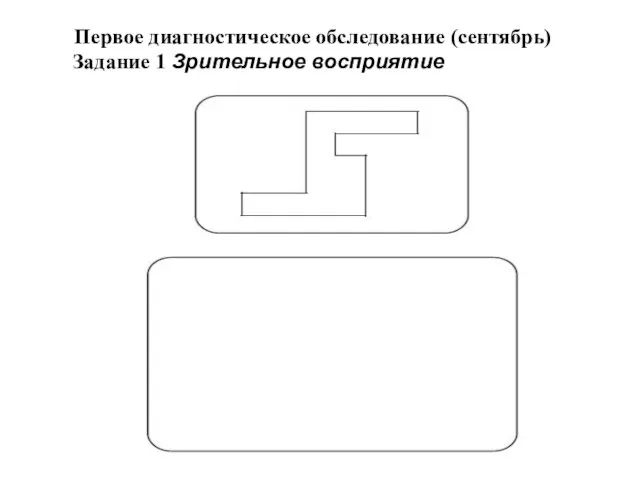
- 186. Первое диагностическое обследование (сентябрь) Задание 1 Зрительное восприятие
- 187. Задание 1 Цель: выявить умение передавать форму фигуры (нарисовать равную или подобную фигуру, соблюдая пропорции между
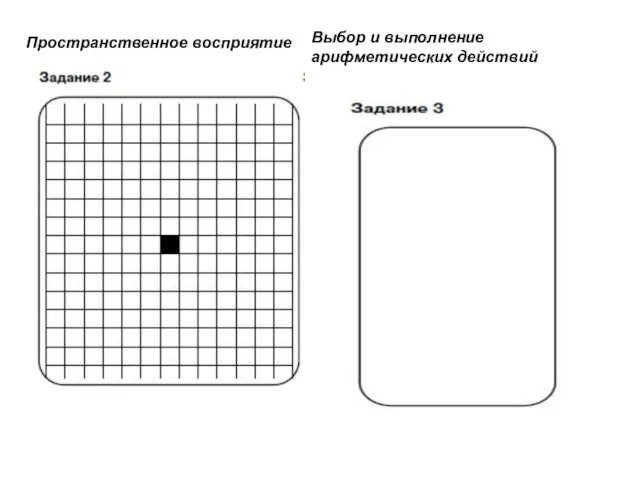
- 188. Пространственное восприятие Выбор и выполнение арифметических действий
- 189. Задание 2 Цель: выявить умение ориентироваться на плоскости (влево, вправо, вверх, вниз). Проверяется также умение пересчитывать
- 190. Задание 3 Цель: выявить умение выбрать и выполнить операцию сложения и вычитания; при умение правильно понять
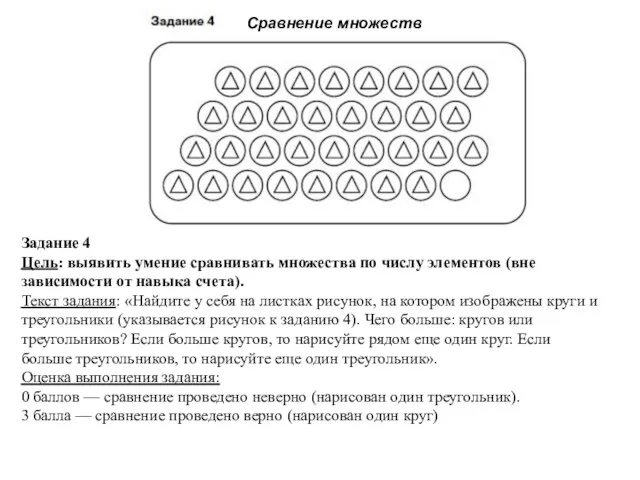
- 191. Задание 4 Цель: выявить умение сравнивать множества по числу элементов (вне зависимости от навыка счета). Текст
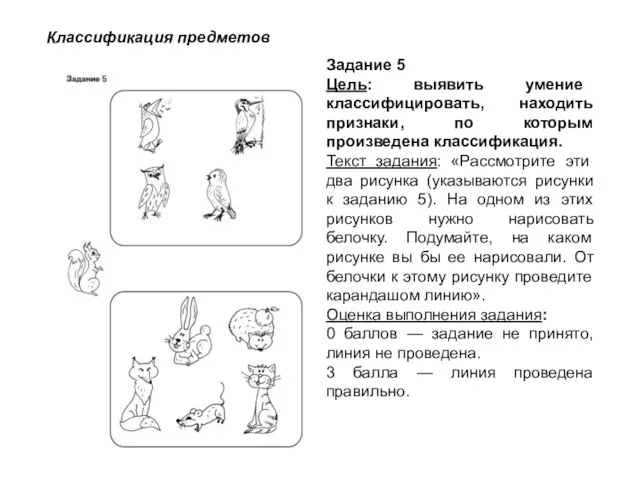
- 192. Задание 5 Цель: выявить умение классифицировать, находить признаки, по которым произведена классификация. Текст задания: «Рассмотрите эти
- 193. http://www.igraemsa.ru/
- 194. http://www.maam.ru/obrazovanie/igry-po-matematike
- 195. http://ideas4parents.ru/mamina_shkola/matematika.html
- 197. Скачать презентацию





































































































































 Управление внутренних дел администрации Московского района г.Минска
Управление внутренних дел администрации Московского района г.Минска Управление закупками государственными автономными и бюджетными учреждениями
Управление закупками государственными автономными и бюджетными учреждениями Презентация на тему: Памятка. Исправление речевых ошибок
Презентация на тему: Памятка. Исправление речевых ошибок Характер и способности
Характер и способности Теоретические основы физиотерапии. Физиопрофилактика. Гальванизация. Электрофорез
Теоретические основы физиотерапии. Физиопрофилактика. Гальванизация. Электрофорез МП
МП Семейная фотосессия
Семейная фотосессия Режущий инструмент
Режущий инструмент Контрольная работа Управление запасами. Расчет параметров поставок
Контрольная работа Управление запасами. Расчет параметров поставок Правила дорожного движения глазами ребенка.
Правила дорожного движения глазами ребенка. Здоровье. Четыре фактора, определяющие состояние индивидуального здоровья
Здоровье. Четыре фактора, определяющие состояние индивидуального здоровья Год науки и технологий. Научные открытия
Год науки и технологий. Научные открытия Автоматизация звука [Ж] в словосочетаниях
Автоматизация звука [Ж] в словосочетаниях Отчет по практике студентов группы Э-143
Отчет по практике студентов группы Э-143 Выявление причин не включения компрессора на одной из секции электропоезда ЭТ2М
Выявление причин не включения компрессора на одной из секции электропоезда ЭТ2М статика и динамика
статика и динамика Диссидентское движение
Диссидентское движение Храмовая архитектура
Храмовая архитектура Качалки и самокачалки для малышей. Мебельная мастерская Adamas
Качалки и самокачалки для малышей. Мебельная мастерская Adamas XII турнир по баскетболу памяти В.П. Видуто
XII турнир по баскетболу памяти В.П. Видуто Что считаетсяизобретением?
Что считаетсяизобретением? Сочинение описание животного 5 класс
Сочинение описание животного 5 класс Основы права. Лекция 8
Основы права. Лекция 8 Презентация на тему Отряд Подёнки
Презентация на тему Отряд Подёнки Самоиндукция
Самоиндукция Модуль MIGRATE и другие средства импорта содержания в Drupal
Модуль MIGRATE и другие средства импорта содержания в Drupal THE KAZAKHSTAN’S MOST ANCIENT ARCHITECTURE: Geoglyphs / The Album of typical examples by Dr. Konstantin I.SAMOILOV. - Almaty, 2016
THE KAZAKHSTAN’S MOST ANCIENT ARCHITECTURE: Geoglyphs / The Album of typical examples by Dr. Konstantin I.SAMOILOV. - Almaty, 2016 Океаны
Океаны