Теорія ймовірностей і математична статистика: описові статистичні показники

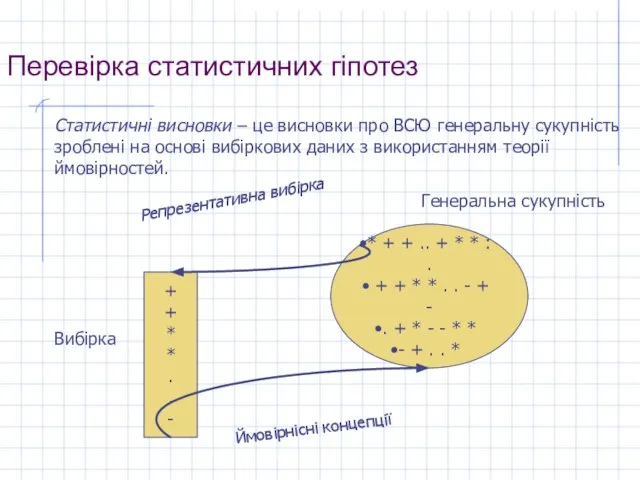
Перевірка статистичних гіпотез
Статистичні висновки – це висновки про ВСЮ генеральну сукупність зроблені на основі вибіркових даних з використанням теорії ймовірностей.
* + + .. + * * : .
+ + * * . . - + -
. + * - - * *
- + . . *
+
+
*
*
.
.
-
Генеральна сукупність
Вибірка
Репрезентативна вибірка
Ймовірнісні концепції

Вступ : типи даних
Кількісні дані: дискретні, неперервні.
Денна кількість відвідувачів: 23, 34, 25, 30, 45.
Ціна на бензин А-95 в різних містах України: 6.42, 6.22, 6.30, 6.52, 6.60.
Якісні дані: порядкові, номінальні.
Кредитний рейтинг: АА+, АА, АА-, А+, А, А-, ВВ+ ....
Список депутатів ВР: ....................................

Вступ : типи даних
Просторів дані та часові ряди.
Просторові дані – дані зібрані в один момент часу з різних об’єктів.
Часові ряди – дані про один об’єкт, що періодично збирались.
Згруповані та незгруповані дані.
Незгруповані дані ціни товару: 3.5, 4, 2.8, 2.5, 2.9.
Згруповані дані ціни товару: дешево – 3, дорого – 2.

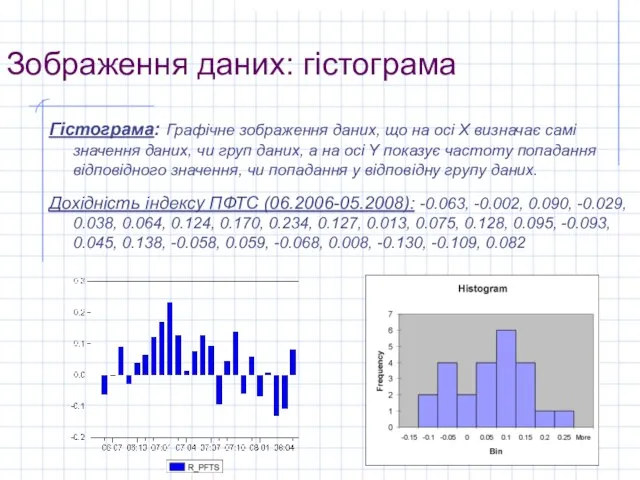
Зображення даних: гістограма
Гістограма: Графічне зображення даних, що на осі Х визначає самі значення даних, чи груп даних, а на осі Y показує частоту попадання відповідного значення, чи попадання у відповідну групу даних.
Дохідність індексу ПФТС (06.2006-05.2008): -0.063, -0.002, 0.090, -0.029, 0.038, 0.064, 0.124, 0.170, 0.234, 0.127, 0.013, 0.075, 0.128, 0.095, -0.093, 0.045, 0.138, -0.058, 0.059, -0.068, 0.008, -0.130, -0.109, 0.082

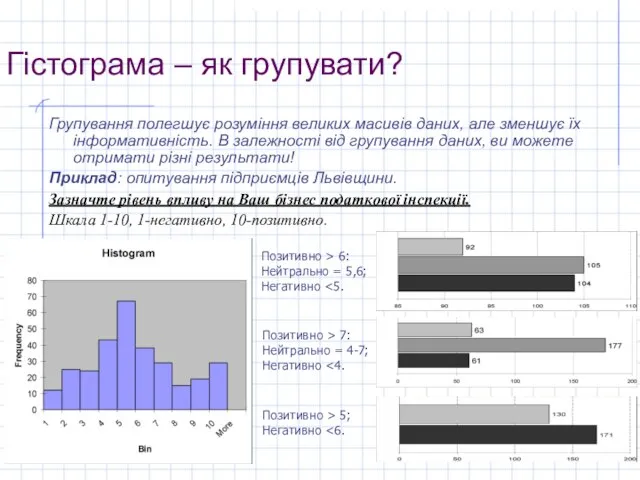
Гістограма – як групувати?
Групування полегшує розуміння великих масивів даних, але зменшує їх інформативність. В залежності від групування даних, ви можете отримати різні результати!
Приклад: опитування підприємців Львівщини.
Зазначте рівень впливу на Ваш бізнес податкової інспекції.
Шкала 1-10, 1-негативно, 10-позитивно.
Позитивно > 6:
Нейтрально = 5,6;
Негативно <5.
Позитивно > 7:
Нейтрально = 4-7;
Негативно <4.
Позитивно > 5;
Негативно <6.

Показники середнього (типового значення)
Середнє значення:
Середнє зважене:
Середнє геометричне:
Медіана – значення, що має порядковий номер (n+1)/2 в ряді даних впорядкованому по зростанню.
Мода – значення, що трапляється найчастіше.

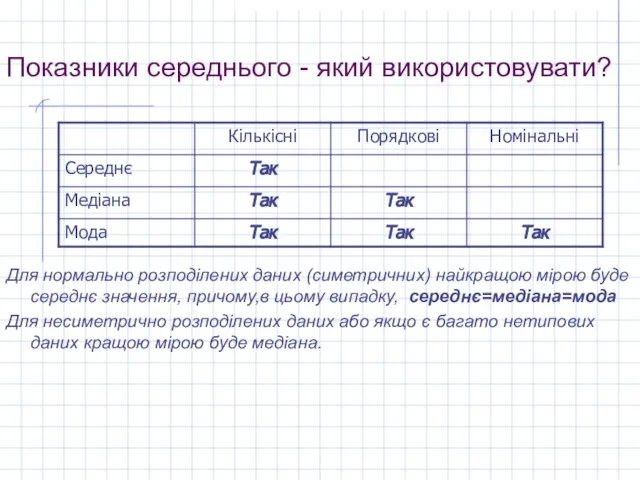
Показники середнього - який використовувати?
Для нормально розподілених даних (симетричних) найкращою мірою буде середнє значення, причому,в цьому випадку, середнє=медіана=мода
Для несиметрично розподілених даних або якщо є багато нетипових даних кращою мірою буде медіана.

Показники розкиду даних
K-тий персентиль – це значення, що відділяє k% даних від решти.
0-ий персентиль = мінімальне значення;
100-ий персентиль = максимальне значення;
50-ий персентиль = медіана.
Нижній квартиль = 25-ий персентиль;
Верхній квартиль = 75-ий персентиль.
Персентилі використовують для:
визначення величини, що відповідає певному персентилю, наприклад, заробітня плата працівника, що відповідає 10-му персентилю становить 1576 грн.
обернено, щоб показати порядковий ранг певного значення з набору даних, наприклад, чистий прибуток філії А склав 50 тис. грн, що відповідає 65-му персентилю.

Показники варіації даних
Стандартне відхилення (середньоквадратичне відхилення):
В Excel – це функція СТОТКЛОН чи STDEV.
Дисперсія = s2.
Коефіцієнт варіації = =
Стандартне відхилення
Середнє
s
X

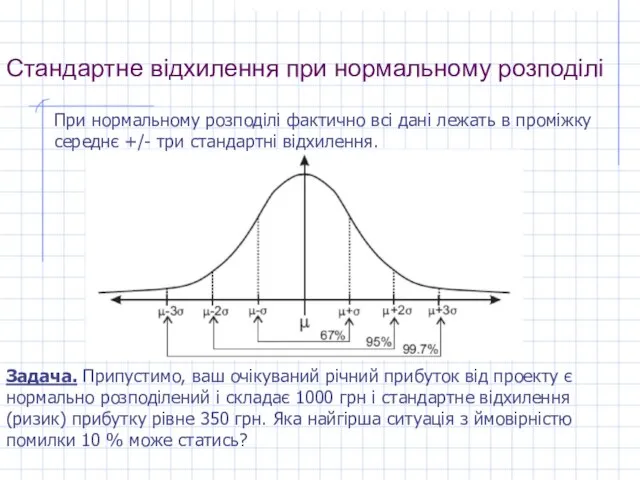
Стандартне відхилення при нормальному розподілі
При нормальному розподілі фактично всі дані лежать в проміжку середнє +/- три стандартні відхилення.
Задача. Припустимо, ваш очікуваний річний прибуток від проекту є нормально розподілений і складає 1000 грн і стандартне відхилення (ризик) прибутку рівне 350 грн. Яка найгірша ситуація з ймовірністю помилки 10 % може статись?

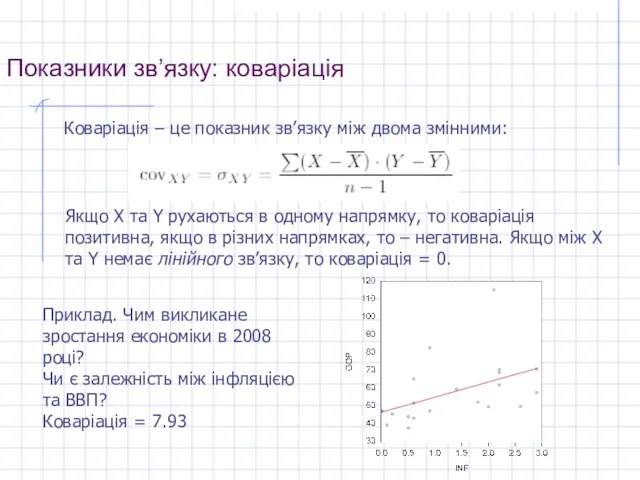
Показники зв’язку: коваріація
Коваріація – це показник зв’язку між двома змінними:
Якщо X та Y рухаються в одному напрямку, то коваріація позитивна, якщо в різних напрямках, то – негативна. Якщо між X та Y немає лінійного зв’язку, то коваріація = 0.
Приклад. Чим викликане зростання економіки в 2008 році?
Чи є залежність між інфляцією та ВВП?
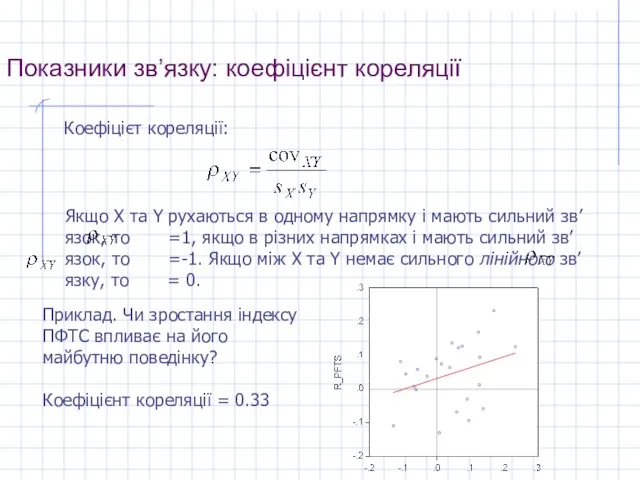
Коваріація = 7.93

Показники зв’язку: коефіцієнт кореляції
Коефіцієт кореляції:
Якщо X та Y рухаються в одному напрямку і мають сильний зв’язок, то =1, якщо в різних напрямках і мають сильний зв’язок, то =-1. Якщо між X та Y немає сильного лінійного зв’язку, то = 0.
Приклад. Чи зростання індексу ПФТС впливає на його майбутню поведінку?
Коефіцієнт кореляції = 0.33