правилами игры действий и его осуществление.
Ходы бывают:
личными – когда игрок сознательно выбирает и осуществляет тот или другой вариант действия (пример –– любой ход в шахматах);
случайными – когда выбор осуществляется не волей игрока, а каким-то механизмом случайного выбора (бросание монеты, игральной кости).
Игры бывают:
парные – игра между двумя игроками;
множественные – в них участники могут образовывать коалиции (постоянные или временные);
кооперативные – играют более двух человек, которые образуют кооперации до конца игры;
коалиционные – объединение, но не до конца игры;
не коалиционные – с начала и до конца каждый играет сам за себя.



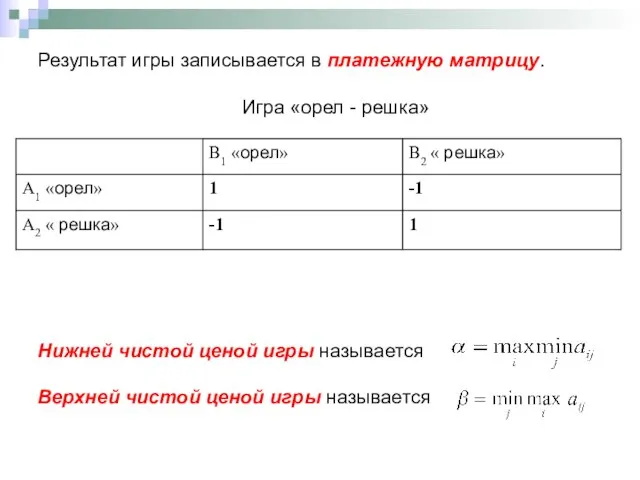







 Как построить гараж?
Как построить гараж? Оптическое просветление биологических тканей – перспективы применения в медицинской диагностике и фототерапии
Оптическое просветление биологических тканей – перспективы применения в медицинской диагностике и фототерапии Дорожное движение, безопасность участников дорожного движения (5 класс)
Дорожное движение, безопасность участников дорожного движения (5 класс) Профессия – ученик
Профессия – ученик Один путь к Богу
Один путь к Богу О денежно-кредитной политике инновационного экономического развития
О денежно-кредитной политике инновационного экономического развития Презентация о стрекозах...
Презентация о стрекозах... Презентация Слива
Презентация Слива Изменения в законе РФ О занятости населения в Российской Федерации. Информация для работодателей
Изменения в законе РФ О занятости населения в Российской Федерации. Информация для работодателей Ян Вермеер Делфтеский (картины)
Ян Вермеер Делфтеский (картины) Законы Кеплера
Законы Кеплера Презентация на тему Как написать сочинение
Презентация на тему Как написать сочинение Презентация на тему Составное глагольное сказуемое
Презентация на тему Составное глагольное сказуемое  Презентация на тему Происхождение человека. Человеческие расы
Презентация на тему Происхождение человека. Человеческие расы  день отца
день отца Тема 2 Система и источники МЧП
Тема 2 Система и источники МЧП Национальные традиции, обычаи, культура народов нашего края
Национальные традиции, обычаи, культура народов нашего края Решение задач повышенного уровня
Решение задач повышенного уровня Як заповнити оціночну форму
Як заповнити оціночну форму История кино. Кинематограф
История кино. Кинематограф Презентация Сущность и функции методологического подхода
Презентация Сущность и функции методологического подхода Stili_rechi_ISP9-21_Sidorov
Stili_rechi_ISP9-21_Sidorov Настольные игры от разработчиков
Настольные игры от разработчиков Куклы - обереги 4 класс
Куклы - обереги 4 класс Прогностика, пророчества и осуществление единственного будущего
Прогностика, пророчества и осуществление единственного будущего О Программе «Национальная банковская система России 2010, 2020»
О Программе «Национальная банковская система России 2010, 2020» Размножение организмов 6 класс
Размножение организмов 6 класс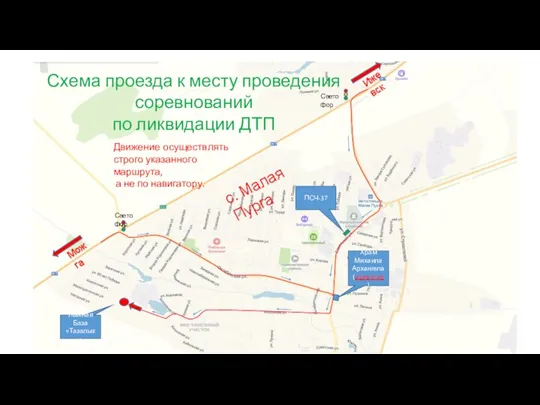 Схема проезда к месту проведения соревнований по ликвидации ДТП, лыжная база Тазалык
Схема проезда к месту проведения соревнований по ликвидации ДТП, лыжная база Тазалык