Теория нормализации

Теория нормализации
Нормализация данных – это декомпозиция (разбиение путем проецирования) отношения, находящегося в предыдущей нормальной форме, на два или более отношений, удовлетворяющих требованиям следующей нормальной формы.
Нормализация данных – это разложение отношений на большее количество более простых таблиц.

Цели нормализации
Основной целью теории нормальных форм первоначально была экономия места на диске.
Данные должны быть устроены так, чтобы при их редактировании или удалении, необходимо было исправлять данные только в одном месте БД.
Группировка данных по содержанию (каждая таблица - определенная тематика).
Принцип модульности (несколько унифицированных независимых блоков).

Первая нормальная форма
Отношение R находится в первой нормальной форме (1NF) тогда и только тогда, когда значения всех его атрибутов атомарны.
Замечания:
Отношение R должно быть регулярно.
Отношение R не должно содержать вычисляемых полей.

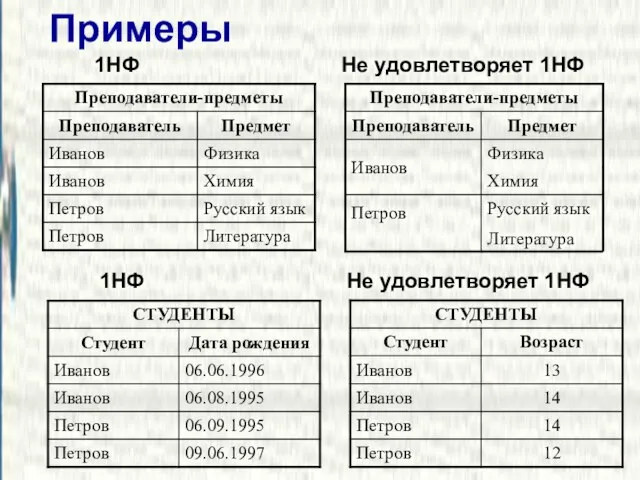
Примеры
1НФ
Не удовлетворяет 1НФ
1НФ
Не удовлетворяет 1НФ

Декомпозиция без потерь
Основой нормализации является процесс разбиения - или декомпозиции. Причем нас будет интересовать не просто процесс декомпозиции, а процесс декомпозиции без потерь.
Определение. Процесс декомпозиции будем называть декомпозицией без потерь, если из полученных отношений можно полностью восстановить исходное отношение без потери информации.
По своей сути декомпозиция представляет собой проекцию. А обратное преобразование - операция соединения.

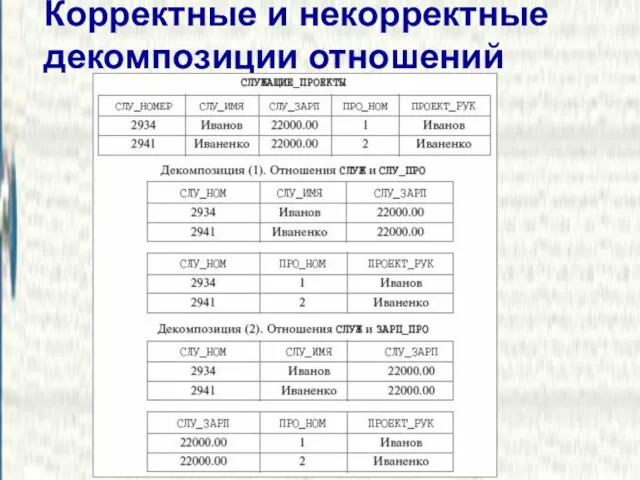
Корректные и некорректные декомпозиции отношений

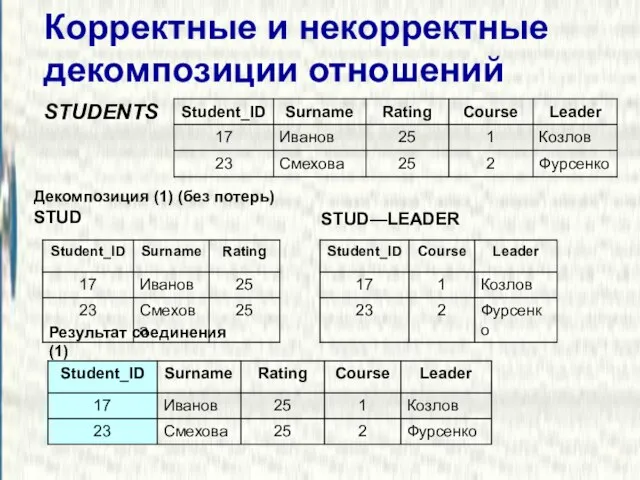
Корректные и некорректные декомпозиции отношений
STUDENTS
Декомпозиция (1) (без потерь)
STUD
STUD—LEADER
Результат соединения (1)

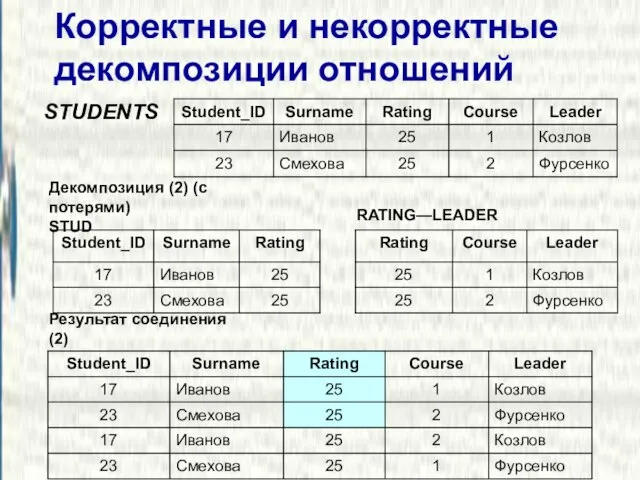
Корректные и некорректные декомпозиции отношений
STUDENTS
Результат соединения (2)
Декомпозиция (2) (с потерями)
STUD
RATING—LEADER

Теорема Хита
Пусть дано отношение r (A, B, C),
где A, B и C – непересекающиеся подмножества множества (в противном случае получим избыточность FD) атрибутов R. Причём множество атрибутов R равно объединению подмножеств A, B, C.
Если R удовлетворяет функциональной зависимости В → С, то R равно естественному соединению его проекций {A, B} и {В, C}.
r = (r PROJECT {A, B}) NATURAL JOIN
(r PROJECT {B, C}).

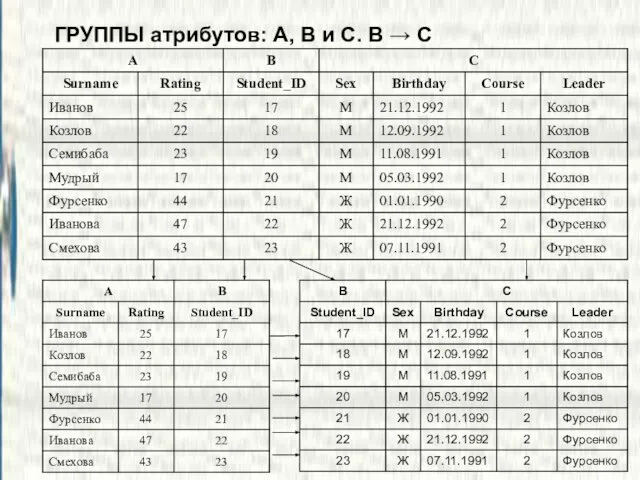
ГРУППЫ атрибутов: A, B и C. B → C

Атрибут B минимально зависит от атрибута A, если выполняется минимальная слева FD A→B.

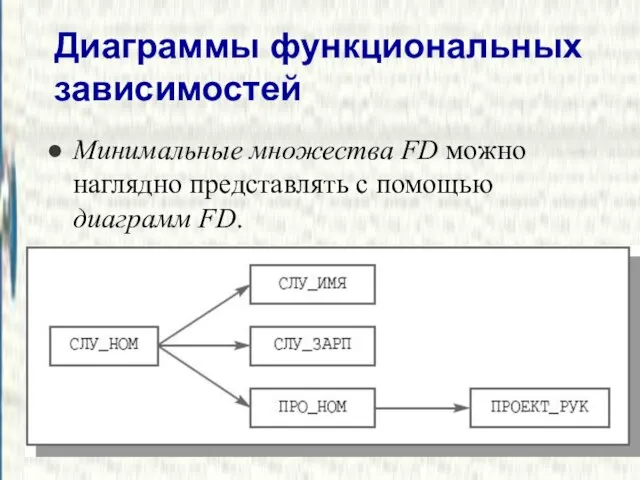
Диаграммы функциональных зависимостей
Минимальные множества FD можно наглядно представлять с помощью диаграмм FD.

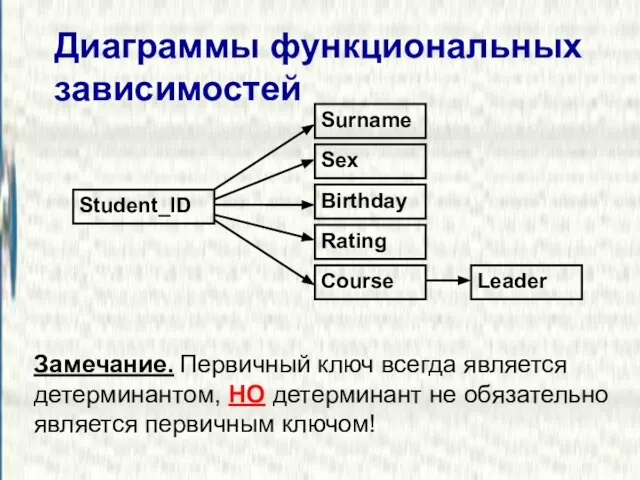
Диаграммы функциональных зависимостей
Замечание. Первичный ключ всегда является детерминантом, НО детерминант не обязательно является первичным ключом!

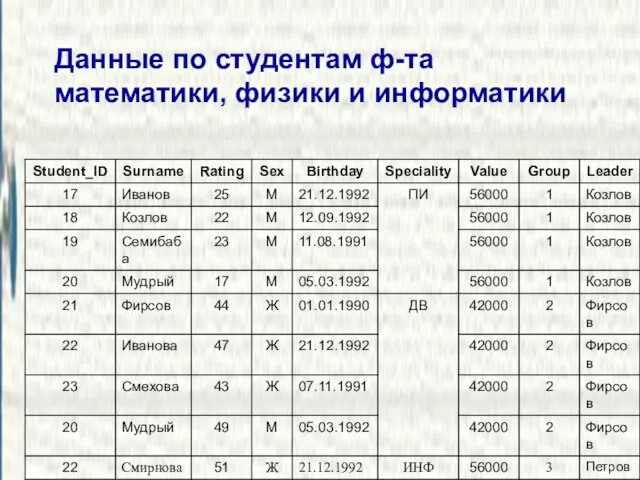
Данные по студентам ф-та математики, физики и информатики

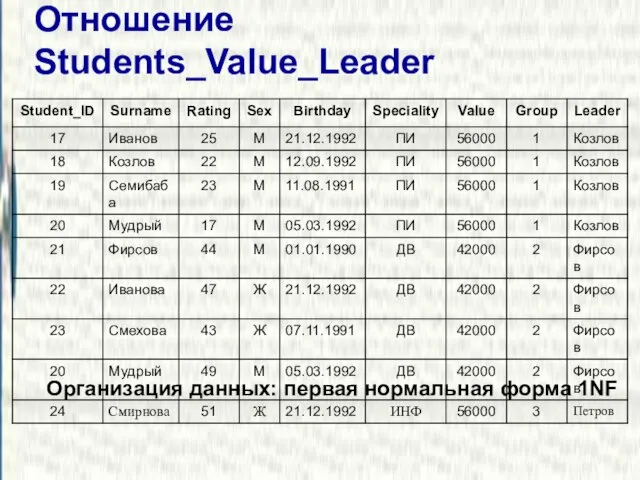
Отношение Students_Value_Leader
Организация данных: первая нормальная форма 1NF

Аномалии модификации
Избыточность данных приводит к следующим аномалиям:
аномалия удаления
аномалия вставки
аномалия модификации
Необходимость нормализации прямо следует из необходимости устранения аномалий

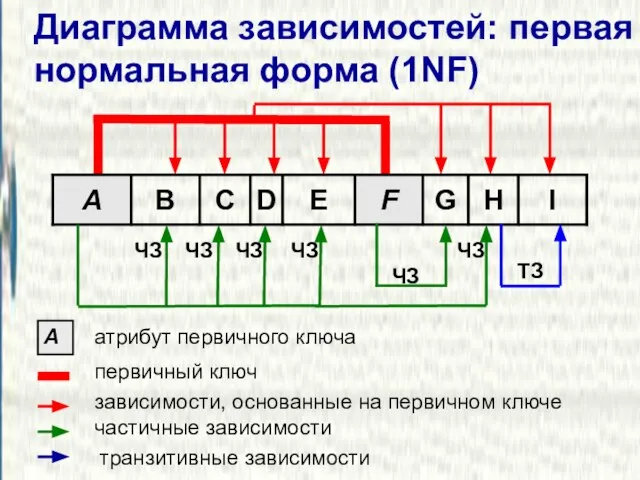
Диаграмма зависимостей: первая нормальная форма (1NF)
A
атрибут первичного ключа
зависимости, основанные на первичном ключе
частичные зависимости
транзитивные зависимости
первичный ключ
ТЗ
ЧЗ
ЧЗ
ЧЗ
ЧЗ

Комментарии к диаграмме зависимостей
Частичная зависимость (partial dependency) – зависимость, определяемая только частью составного первичного ключа.
Транзитивная зависимость (transitive dependency) – зависимость одного непервичного атрибута от другого непервичного атрибута.
Замечание: транзитивные зависимости могут стать причиной аномалии данных.

Приведение к 1NF
Таблица приведена к 1NF, если в ней:
определены все ключевые атрибуты;
отсутствуют повторяющиеся группы (на пересечении каждого столбца и каждой строки содержится только одно (атомарное) значение);
все атрибуты зависят от первичного ключа.
Замечания:
Отношение должно быть регулярно.
Отношение не должно содержать вычисляемых полей.
3. Все реляционные таблицы удовлетворяют требованиям, предъявляемым к 1NF.

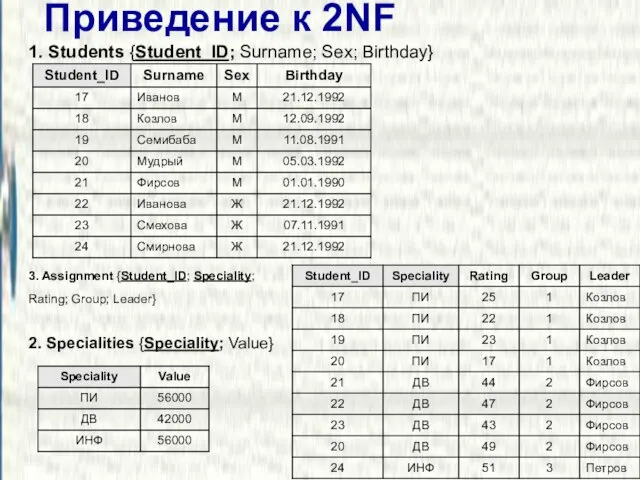
Приведение к 2NF
1. Students {Student_ID; Surname; Sex; Birthday}
2. Specialities {Speciality; Value}
3. Assignment {Student_ID; Speciality;
Rating; Group; Leader}

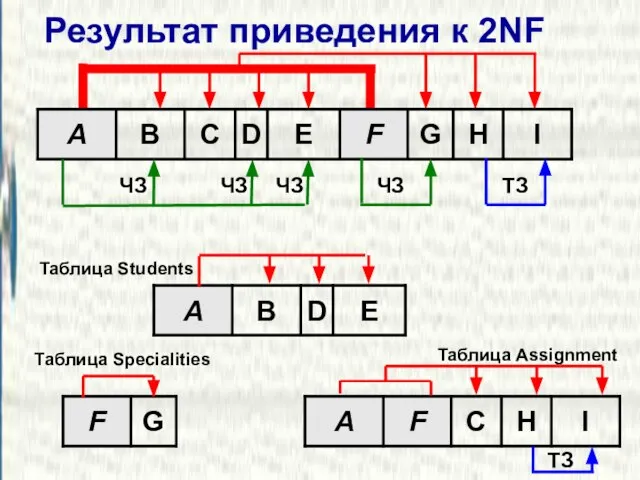
Результат приведения к 2NF
ТЗ
ЧЗ
ЧЗ
ЧЗ
ЧЗ
Таблица Assignment
Таблица Specialities
Таблица Students
ТЗ

Приведение к 2NF
Таблица приведена к 2NF, если:
она приведена к 1NF;
в ней отсутствуют частичные зависимости.
Замечания:
В таблицах, приведённых к 2NF, может иметь место транзитивная зависимость.
Таблицы, в которых первичный ключ содержит всего лишь 1 атрибут, автоматически будут иметь 2NF, если они имеют 1NF.

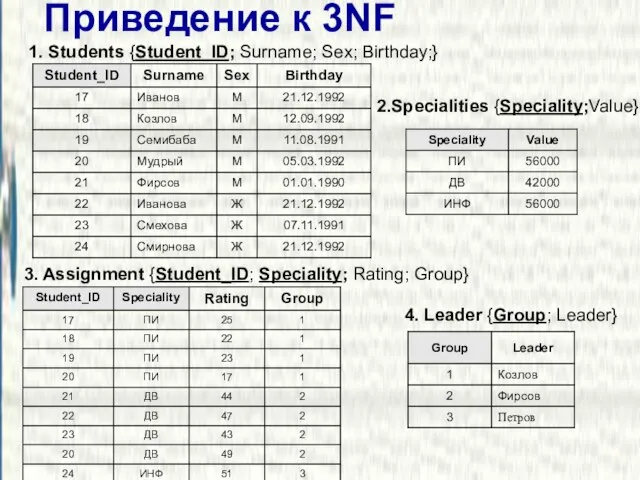
Приведение к 3NF
1. Students {Student_ID; Surname; Sex; Birthday;}
2.Specialities {Speciality;Value}
3. Assignment {Student_ID; Speciality; Rating; Group}
4. Leader {Group; Leader}

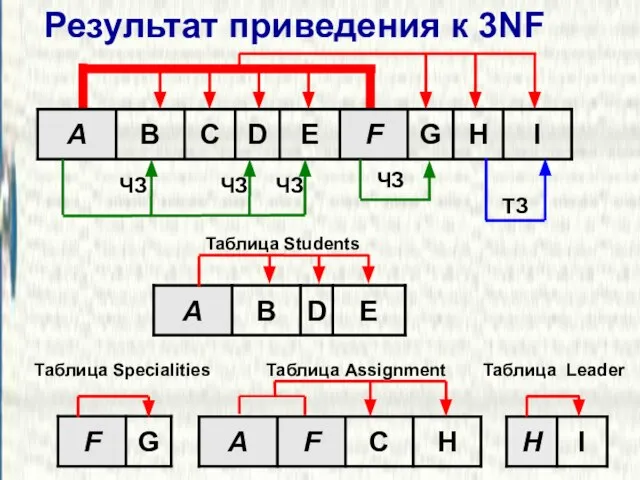
Результат приведения к 3NF
ТЗ
ЧЗ
ЧЗ
ЧЗ
ЧЗ
Таблица Assignment
Таблица Specialities
Таблица Students
Таблица Leader

Приведение к 3NF
Таблица приведена к 3NF, если:
она приведена к 2NF;
в ней отсутствуют транзитивные зависимости.

Нормальная форма
Бойса-Кодда (BKNF)
Таблица приведена к BKNF, если:
она приведена к 3NF;
каждый детерминант таблицы является потенциальным ключом.
Замечание.
Если таблица содержит только один потенциальный ключ, то формы 3NF и BKNF эквивалентны.

Необходимость приведения 3NF к BKNF
Если неключевой атрибут является детерминантом ключевого атрибута, это удовлетворяет требованиям отношения в 3NF форме, но не отвечает правилам BKNF.
A + B → C, D
C → B (неключевой атрибут определяет часть первичного ключа, зависимость нетранзитивна)

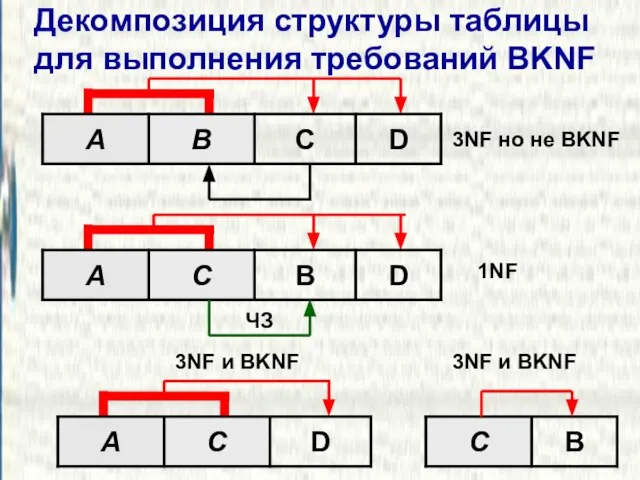
Декомпозиция структуры таблицы для выполнения требований BKNF
3NF но не BKNF
ЧЗ
1NF
3NF и BKNF
3NF и BKNF

Пример
Рассмотрим отношение R:

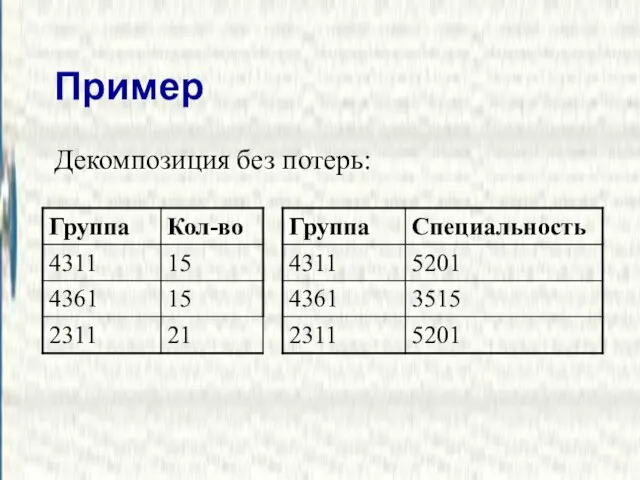
Пример
Декомпозиция без потерь: