Теория вероятностей, математическая статистика и случайные процессы(ТВ, МС и СП)

Измеримые пространства
Вероятностное пространство, определяемое алгебраической системой в виде кортежа из трех множеств: (Ω, A, P), является одним из видов измеримого пространства. В общем случае измеримое пространство – множество Х , на котором задана некоторая мера.
Мера множества – неотрицательная аддитивная функция μ( X ) множества из семейства его подмножеств , обладающая свойствами:
μ(X)≥ 0 , мера – это неотрицальное число,
μ(X1)+ μ(X2) = μ(X1 U X2), если X1 ∩ X2 =Ø;
, , Xi , Xj ∈

Примеры мер
Пример меры для множества действительных чисел: R(1) - длина отрезка.
Ei = [ ai, bi], ai ≤ bi , μ(Еi) = bi - ai , или μ(Еi) = |bi - ai |. (Евклидово пространство измеримо). Аналогично можно распространить данную меру на двух, трех мерное и т.д. пространства. Такими мерами могут быть площадь, объем областей в Евклидовом пространстве.
Для конечных множеств их мерой может служить количество элементов: μ(А(n))=n=|А(n)|.
Действительно если A(n1) ∩ A(n2) =Ø, то μ(A(n1))+ μ(A(n2)) = μ(A(n1) U A(n2)) = n1 + n2 (правило сложения комбинаторики).

Геометрическая модель ВЭ
Вероятностное пространство равновозможных исходов (Ω,A*, P*), является одним из видов измеримого пространства, в котором = Ω и μ(Аj)=P*(Aj) (вероятностная мера Р*).
Например, в Евклидовом двух мерном пространстве действительных чисел (на плоскости xOy), исходом могут служить (x, y) - координаты точки плоскости,
множеством исходов – замкнутая область Ω ={(x,y)|Ω(x,y) ≤0},
событием – замкнутая область A={(x,y)|А(x,y)≤0 }, A⊆ Ω;
вероятностной мерой – Р*= S(А)/S(Ω), т.е. отношением площади области А (S(А) ) к площаде области Ω (S(Ω)).
Эту величину называют геометрической оценкой вероятности случайного события А.
На рисунке приведена модель ВЭ:
«Стрельба по прямоугольному щиту
с круглой мишенью»
y
x
O

Геометрическая оценка вероятности
В общем случае измеримых пространств с равновозможными исходами вероятностная мера определяется формулой:
Р*геом (А)= ,
где mes( * ) – мера измерения геометрических характеристик областей пространства, соответствующих событий.
Она применима для непрерывных вероятностных пространств, когда события (множество исходов) представляются бесконечными несчетными множествами мощности «континуум)

Аксиомы теории вероятности (аксиомы Колмогорова).

Основные свойства вероятности
Рассмотрим основные свойства вероятностной меры (вероятности), которые представляют собой теоремы или следствия, выводимые из аксиом (теорем) ТВ и тождеств алгебры множеств. Обычно в теории вероятностей это называют алгеброй событий.
Свойство 1) P(Ø) = 0 . Следствие: ∀Aj ∈  P(Aj) ∈ [ 0,1].
Доказательство:
Из алгебры множеств известно: Ω+Ø=Ω, Ω ∩ Ø = Ø.
По третьей аксиоме теории вероятности имеем:
P(Ω+Ø)=P(Ω)=1, P(Ω)+P(Ø)=P(Ω), 1+P(Ø)=1, P(Ø)=0 (что и требовалось доказать.

Формула вычитания вероятностей.
Свойство 2.
Пусть = Ω \A , тогда P ( ) = 1 – P(A).
Следствие : Если А ⊆ B , то P(B\A) = P(B) – P(A). (Формула вычитания вероятностей).
Доказательство следствия:
(А ⊆ B) → (B=AU(B\A)) (по теореме Алгебры Мн-в),
по аксиоме (3) ТВ , так как A∩(B\A) = Ø, то P(B)=P(A(B\A) )=P(A)+P(B\A).
Из последнего равенства следует: P(B\A)= P(B) – P(A)
(что и требовалось доказать).

Формула сложения вероятностей
Свойство 3.
P(A U B) = P(A) + P(B) – P(A∩B).
Следствие: (Формула сложения вероятностей)
Если A∩B=Ø , то P(A U B) = P(A) + P(B)
Свойство 4. ∀Aj
Свойство 5.
∀Aj
Свойство 6. ∀A,В (А ⊆ B) → ( P(A) ≤ P(B) )

Свойство непрерывности вероятности
Для последовательности вложенных событий :
Если А1⊆ A2 ⊆ …. ⊆ An ⊆ … , то
;
Для последовательности расширяющихся событий :
Если А1⊇ A2 ⊇ …. ⊇ An ⊇ … , то .
Ω
An
An-1
A1
Ω
A1
A2
An

1.5 Основные виды событий
( Содержательное наполнение теоретико-множественных понятий алгебры событий)
Три составляющие алгебры событий:
Задание аксиом ТВ, определяющих свойства вероятностного пространства (вероятностей);
Содержательное наполнение теоретико-множественных понятий вероятностного пространства (алгебры событий);
Математические средства и методы вычисления вероятностей, тождественно-истинные преобразования формул алгебры событий.

Основные виды событий
Для удобства содержательной интерпретации теоретико-множественных понятий вероятностного пространства (моделей ВЭ) в алгебре событий за множествами с определенными свойствами закреплены определенные названия видов событий. Использование названий событий (терминология) значительно упрощает содержательную интерпретацию математических моделей ВЭ. Многообразие понятийных категорий определяет содержательное богатство формальных теорий, в частности алгебы событий.
Основными видами событий являются: случайное, элементарное, сложное, невозможное, достоверное, противоположное, совместное, зависимое и прочие.

Классификация случайных событий
1) Случайным (произвольным) событием называется любое множество A∈ A, обладающее свойствами :
А ={ω1, ω2, … ,ωm | ωj∈Ω, ∀i≠j ωi∩ ωj =Ø}= ,
P(A)= , P(A) ∈ [ 0,1,]. Если А=В, то Р(А) = Р(В).
2) «Элементарное (простое) случайное событие» называется случайное событие, содержащее только один исход. Символически это можно выразить: A = ω (m=1), P(ω) ∈ [ 0,1]. Для простоты, прилагательное случайное в названиях событий будем опускать, предполагая, что все далее сказанное относится прежде всего к случайным событиям.
Противоположное этому понятию, является понятие сложного (составного) события: - при m > 1 событие А называется сложным.
3) Равновозможные (исходы) события : Вероятности равновозможных событий равны

Классификация случайных событий
4) Невозможное событие - событие, которое не может произойти ни при каком исходе ВЭ. Ему соответствует пустое множество и символически его обозначают символом Ø. Свойство в вероятностном пространстве:
Р(Ø) = 0.
5) Достоверное событие – событие которое происходит каждый раз, когда осуществляется ВЭ. Символически его обозначают символом Ω. Ему соответствует множество исходов.
P(Ω)=1.

Распределение вероятностей
Достоверное событие очень важное понятие, обеспечивающее связь вероятностных экспериментов с детерминированными (вероятностного пространства с детерминированным). С вероятностными свойствами достоверного события связано еще одно фундаментальной понятие ТВ – распределение вероятностей:
{ (ωi, P(ωi)) | ωi∈Ω, =1 } ,
( ∀i≠j ωi∩ ωj =Ø, , P(Ω)= =1 ).
Оно обладает замечательным свойством: любой ВЭ эксперимент может быть однозначно описан в вероятностном пространстве распределением вероятностей! На основе распределения вероятностей можно без особого труда определить множество Р вероятностного пространства, причем для этого потребуется всего n значений вместо 2n
Определение. Множество событий H ={H1, H2, …,HK} образуют полную группу событий если события Нi обладают свойствами:
.

Классификация случайных событий
Над событиями, как над множествами можно выполнять различные операции, например: ∩, U, \ и получать, таким образом новые сложные события и новые их виды.
6) Противоположное событие А – в символической форме оно определяется:
= Ω \A , P( ) = 1 – P(A).
7) События А и В называются несовместными, если А∩ В =Ø. Р(А∩ В) = 0.
Теорема: Противоположные события несовместны: А∩ = Ø. Док-во. Самостоятельно!
8) События А и В называются зависимыми, если Р(А∩В) ≠ 0.
События А и В называются независимыми, если Р(А∩В)= Р(А)*Р(В)≠ 0.
Далее на последующих лекциях мы будем знакомиться с новыми видами событий

Приложение
Основы теории множеств
Множество – это первичное неопределяемое понятие математики (как, например, точка в геометрии). Слова «набор», «совокупность», «семейство» употребляют в качестве его синонимов.
Пример 1. Множествами являются:
– набор из десяти арабских цифр;
– совокупность учащихся института;
– семейство бобовых;
– множество людей на Земле;
– множество действительных чисел.

Используемые обозначения
Множество может состоять из любых различимых объектов (чисел, букв, людей, растений…). Эти объекты называются элементами данного множества. Элементы множества обозначаются строчными буквами латинского алфавита. Если данный объект x является элементом множества X, то говорят, что x принадлежит X (обозначается: x ∈X). В противном случае говорят, что x не принадлежит X (обозначается: x∉X). Для обозначения множеств используются заглавные буквы латинского алфавита.
Множество, не содержащее ни одного элемента, называется пустым (обозначается: ∅ ). Множества, состоящие из конечного числа элементов, называются конечными и обозначать: А(n) (например, первые 4 множества из примера 1). Аналогично, множества, состоящие из бесконечного числа элементов, называются бесконечными (например, последнее множество из примера 1). Мы будем рассматривать, в основном, конечные множества.

Способы задания множества:
1) перечислить все элементы этого множества;
2) указать свойство, которым обладают только элементы этого множества (характеристическое свойство);
3) описать метод (алгоритм) построения этого множества (порождающую процедуру).
Пример 2. Множество С сигналов светофора можно задать первым способом, просто выписав их названия, неважно в каком порядке. Будем делать это так: С = {красный, желтый, зеленый}.

Пример 3. Множество K квадратов можно задать вторым способом, указав, что это совокупность всех прямоугольников, у которых длины всех сторон равны. Формальная запись такова:
K = { Прямоугольники | Длины всех сторон равны }.
Пример 4. Множество X корней уравнения x2-5x+6=0 можно задать третьим способом, описав метод нахождения его элементов, например, графический: построить график функции f(x)=x2-5x+6 в координатной плоскости Oxy и найти точки его пересечения с осью Ox. Множество X можно задать и первыми двумя способами:
1) X = {2, 3};
2) множество чисел, при подстановке каждого из которых вместо x, уравнение x2-5x+6=0 превращается в верное равенство; формально это выглядит так: X = {x | x2-5x+6=0}.

Равенство множеств
Множества A и B называются равными, если их элементы совпадают (обозначается: A=B, в противном случае – A≠B ). Множество A называется подмножеством множества B, если каждый элемент множества А является элементом множества B (обозначается: A ⊆ B). При этом говорят, что A содержится в B, а B включает A. Если A ⊆ B и A≠B, то A называется собственным подмножеством B (обозначается: A⊂ B). Пустое множество содержится в любом множестве. Любое множество является своим подмножеством (несобственным). Теперь можно дать другое определение равенства множеств: A=B, если A ⊂ B и B ⊂ A.
Обычно, в каждом конкретном случае берется некоторое множество U (универсум), которое включает все рассматриваемые множества. В следующих 4-х определениях операций над множествами предполагается A ⊆ U, B ⊆ U.

Операции над множествами
Пересечением множеств A и B называется множество, каждый элемент которого принадлежит и A, и B одновременно (обозначается A∩B). A ∩ B = AB= {x | x∈ A и x∈ B}.
Обычно дают следующую графическую интерпретацию этого определения. Универсум изображают в виде прямоугольника, внутри которого кругами изображают рассматриваемые множества. Точки, лежащие внутри кругов можно рассматривать как элементы соответствующих множеств. Пересечением множеств будет заштрихованная область, общая для обоих кругов (см. рис.1). Полученное изображение называют диаграммой Эйлера-Венна.
рис.1

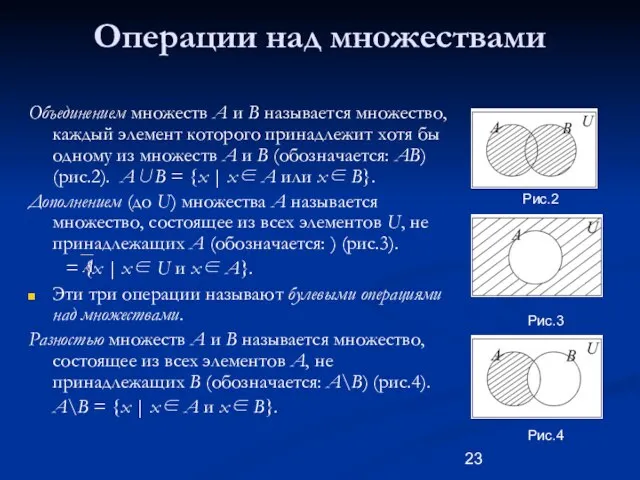
Операции над множествами
Объединением множеств A и B называется множество, каждый элемент которого принадлежит хотя бы одному из множеств A и B (обозначается: AB) (рис.2). A∪B = {x | x∈ A или x∈ B}.
Дополнением (до U) множества A называется множество, состоящее из всех элементов U, не принадлежащих A (обозначается: ) (рис.3).
= {x | x∈ U и x∈ A}.
Эти три операции называют булевыми операциями над множествами.
Разностью множеств A и B называется множество, состоящее из всех элементов A, не принадлежащих B (обозначается: A\B) (рис.4).
A\B = {x | x∈ A и x∈ B}.
Рис.2
Рис.3
Рис.4

Свойства операций над множествами.
1. A=A.
2. Свойства дополнения:
A ∩A= ∅ A∪A =U
3. Идемпотентность:
A ∩ A=A A∪A=A
4. Коммутативность:
A ∩ B=B∩A A∪B=B∪A
5. Ассоциативность:
(AB)C=A(BC)
(AB)C=A(BC)
6. Дистрибутивность:
A(BC)=(AB)(AC)
A(BC)=(AB)(AC)
7. Поглощение:
A∩(B∪A)=A A∪(B∩A)=A
8. Свойства U:
A∩U=A A∪U=U
9. Свойства ∅:
A ∩ ∅ = ∅ A ∪ ∅ =A
10. Законы де Моргана:
11. Инволютивность:
=A
12. Связь U с ∅ :
=∅ = U
13. Связь операций :
A\B = A∩B