Тетраэдр, виды сечений и решение задач по тетраэдру

Цель работы:
Выяснить какие виды сечений тетраэдра существуют
Терминология
Показать на примерах решения задач тетраэдра

Терминология:
Тетраэдр – поверхность, составленная из четырех треугольников
Сечение – многоугольник, образованный при пересечении граней тетраэдра секущей плоскостью, сторонами которого являются отрезки по которым они пересекаются.

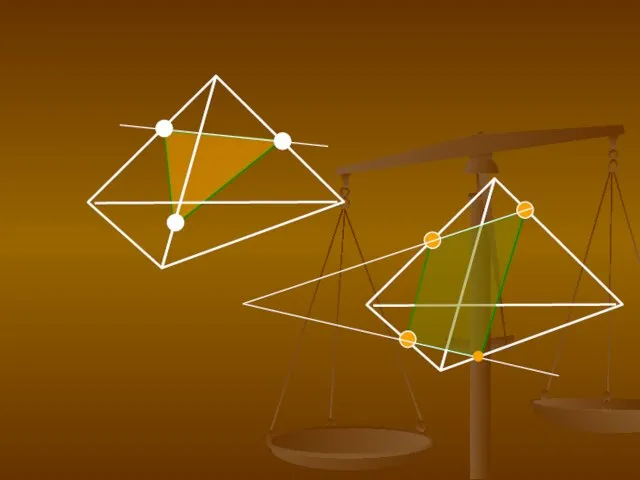
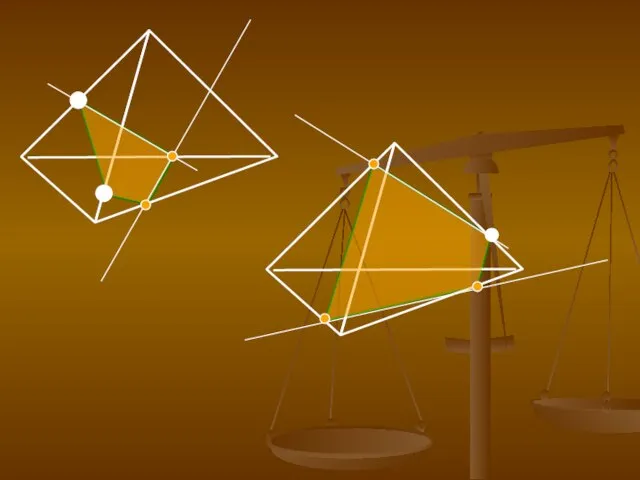
Виды сечений:

Геометрическое утверждение
Если две точки одной прямой лежат в плоскости, то и
вся прямая лежит в этой плоскости.

Задача №1
Назовите все пары скрещивающихся
(т.е.принадлежащих скрещивающимся прямым) ребер тетраэдра ABCD. Сколько таких пар ребер имеет тетраэдр?

Решение:
В тетраэдре три пары скрещивающихся ребер:
AC и DB;AB и DC;AD и CB.
D
B
C
A

Задача №2
Точки М и N – середины ребер AB и BC тетраэдра ABCD. Докажите, что прямая MN параллельна плоскости BCD.

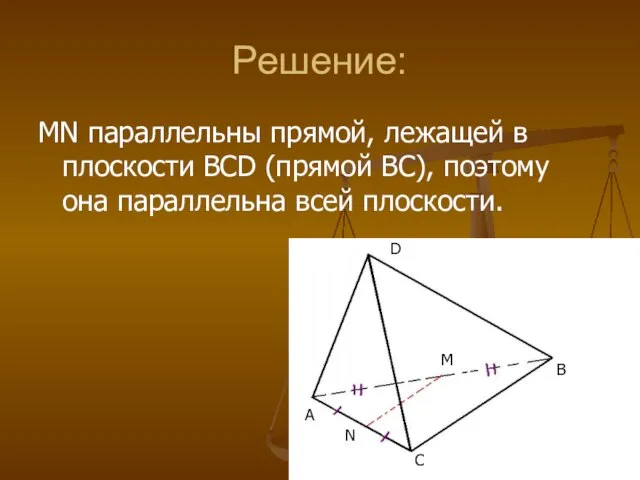
Решение:
MN параллельны прямой, лежащей в плоскости BCD (прямой BC), поэтому она параллельна всей плоскости.
A
C
B
D
M
N

Задача №3
Через середины ребер AB и BC тетраэдра SABC проведена плоскость параллельно ребру SB. Докажите , что эта плоскость пересекает грани SAB и SBC по параллельным прямым.

Решение:
Плоскость SBC и плоскость, проходящая через прямую MN параллельно ребру SB, пересекаются по прямой, проходящей через точку N.
По теореме линия пересечения параллельна SB.
В плоскости SBC через т.N проходит NQ SB.
Плоскость SAB и плоскость MNQ пересекаются по прямой, проходящей через т. М(прямая MP).
По теореме линия пересечения параллельна SB.
PM SB
NQ SB
PM NQ.
Утверждение доказано.
S
B
C
N
A
P
Q
M

Заключение:
В результате работы над темой я изучил терминологию , виды сечения. Рассмотрел задачи на построение сечений , предложенных в различных спецкурсах по геометрии.