Технология решения экономических задач в Excel

Операции с массивами в табличном процессоре
Массив – набор данных одного типа. Массив в Excel хранится в диапазоне ячеек. Адресная ссылка на диапазон имеет формат:
<адрес начальной ячейки диапазона >:< адрес конечной ячейки>,
например, А2:С5.
Массив также может быть задан именем диапазона (1 – выделить диапазон и в поле имени записать идентификатор; 2 – Вставка/Имя/Присвоить)
Excel позволяет создавать одномерные (вектора), двумерные (матрицы), трехмерные массивы.
Чтобы указать, что производится операция над массивом, следует нажать комбинацию клавиш Ctrl+Shift+Enter.

Операции с массивами в табличном процессоре
Пример. Умножить элементы массива размерностью 2×2 на число 3 в электронной таблице. Исходный массив
Решение
Введем в ячейки диапазона A1:B2 значения элементов массива. Выделим диапазон ячеек D1:E2 такой же размерности, в которой будет помещаться результат операции. Введем в выделенный диапазон формулу в формате:
=<адрес начальной ячейки диапазона >:< адрес конечной ячейки диапазона >*< адрес второго операнда >,
т.е. =A1:B2*3
Нажмем комбинацию клавиш Ctrl+Shift+Enter. В ячейках выделенного диапазона появится результат.

Операции с массивами в табличном процессоре
Операции с векторами:
Вычисление суммы векторов
Вычисление произведения вектора на число
Вычисление скалярного произведения векторов (=СУММ(Вектор1*Вектор2))
Операции с матрицами:
Умножение матрицы на число
Суммирование и вычитание матриц

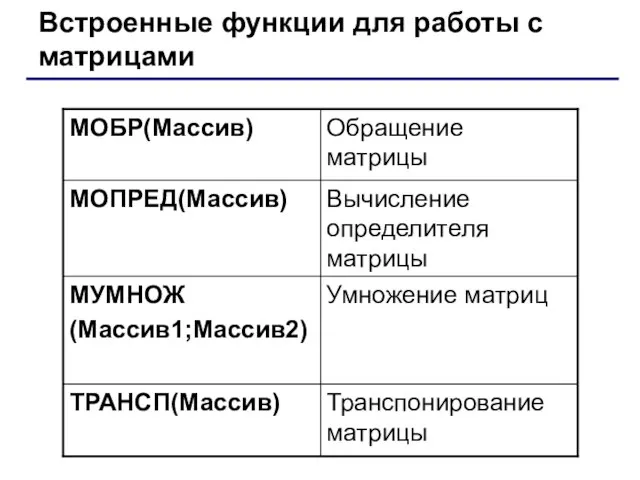
Встроенные функции для работы с матрицами

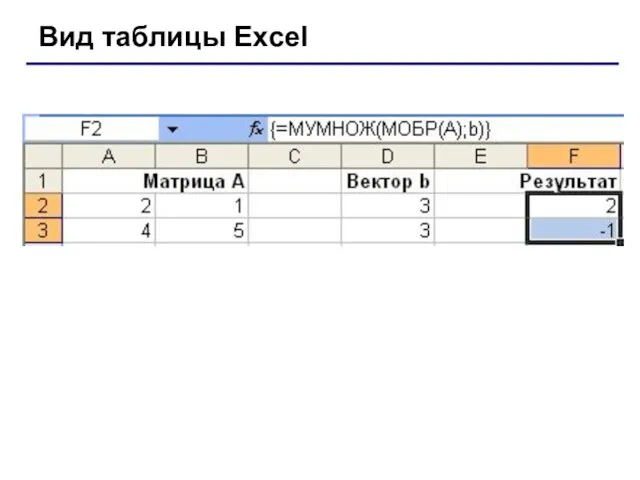
Пример. Система уравнений Ax = b задана матрицей А и вектором b.
Решить систему методом обратной матрицы:
Решение. Присвоим диапазону А2:В3 имя (например, А) и введем значения элементов матрицы. Присвоим диапазону имя D2:D3 имя (например, b) и введем значения элементов вектора.
Выделим диапазон F2:F3 и введем в него формулу МУМНОЖ(МОБР(А);b). Нажмем комбинацию клавиш Ctrl+Shift+Enter. В ячейках выделенного диапазона появится результат.
Решение систем линейных уравнений

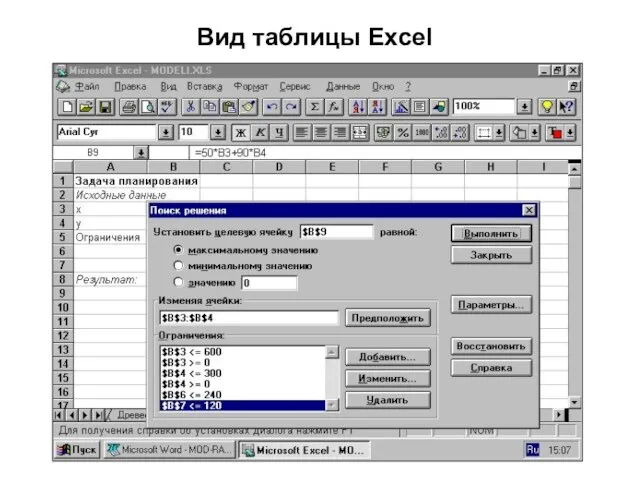
Вид таблицы Excel

Решение систем линейных уравнений методом наименьших квадратов
Пример. Требуется решить систему уравнений
Применяется, когда число столбцов матрицы не совпадает с числом строк

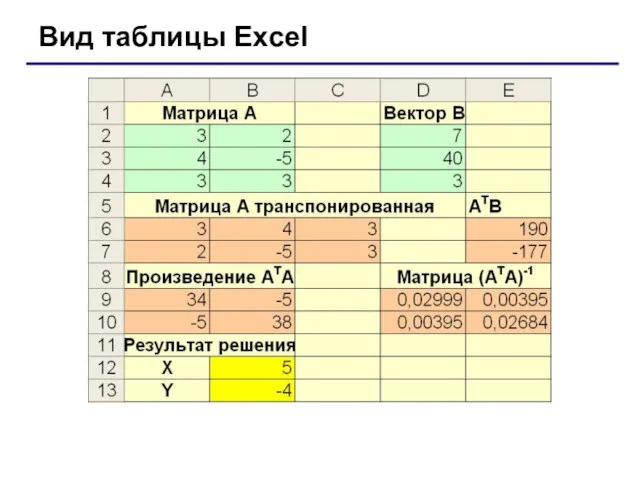
Введем значения элементов матрицы А в диапазон А2:В4, вектора В в ячейки D2:D4.
Транспонируем матрицу А: выделяем диапазон размерностью 2×3 А6:С7, вводим функцию ТРАНСП(А2:В4), нажимаем комбинацию клавиш Ctrl+Shift+Enter.
Вычисляем произведение матрицы АT и вектора В: выделяем диапазон Е6:Е7, вводим функцию МУМНОЖ(А6:С7;D2:D4), нажимаем комбинацию клавиш Ctrl+Shift+Enter.
Вычисляем произведение матриц АT и А: выделяем диапазон А9:В10, вводим функцию МУМНОЖ(А6:С7;А2:В4), нажимаем комбинацию клавиш Ctrl+Shift+Enter.
Вычисляем обратную матрицу (АTА)-1: выделяем диапазон D9:E10, вводим функцию МОБР(А9:В10).
Вычисляем результат: выделяем диапазон В12:В13, вводим функцию МУМНОЖ(D9:E10; Е6:Е7).
Решение в Excel

Вид таблицы Excel

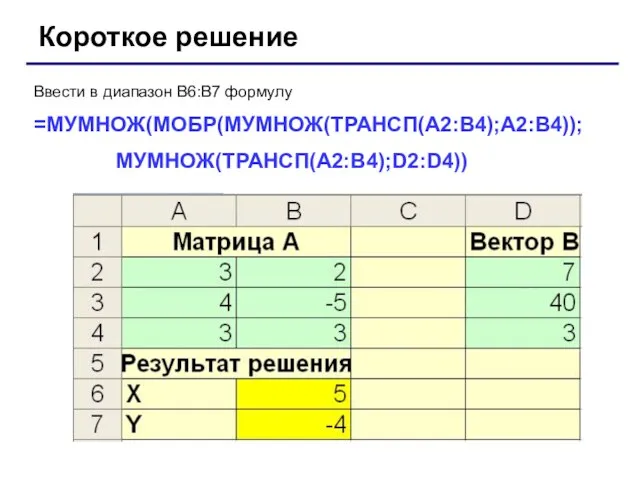
Ввести в диапазон В6:В7 формулу
=МУМНОЖ(МОБР(МУМНОЖ(ТРАНСП(A2:B4);A2:B4));
МУМНОЖ(ТРАНСП(A2:B4);D2:D4))
Короткое решение

Анализ данных в электронных таблицах Excel

Инструмент Подбор параметра
Подбор параметра – инструмент анализа «что-если», когда желаемый результат одиночной формулы известен, но неизвестны значения, которые требуется ввести для получения этого результата.
Сервис/Подбор параметра
При подборе параметра Microsoft Excel изменяет значение в одной конкретной ячейке до тех пор, пока формула, зависимая от этой ячейки, не возвращает нужный результат.

Решение уравнений с использованием
подбора параметра
Пример 1
Все ученики класса обменялись своими фотографиями. Всего было передано друг другу 756 фотографий. Сколько человек в классе?
РЕШЕНИЕ
Математическая модель
Пусть в классе N учеников. Каждый из них отдал N-1 фотографию. Следовательно, всего отдано N*(N – 1) фотографий.
Получаем уравнение:
N*(N – 1) = 756

Технология решения задачи
Первый способ – Подбор параметра
В ячейку А1 занести текст: “Учеников в классе -”
В ячейку А2 занести текст: “Фотографий”
2. В ячейку В2 занести формулу: =В1*(В1-1)
3. Вызвать меню СЕРВИС / ПОДБОР ПАРАМЕТРА. Установить требуемые реквизиты в следующем виде:
Получим

Второй способ – ПОИСК РЕШЕНИЯ
Надстройка «Поиск решения»
Надстройка – вспомогательная программа, служащая для добавления в MS Excel специальных команд или возможностей. Может быть загружена либо только для текущего сеанса, либо для каждого сеанса работы в Microsoft Excel.
Загрузка надстройки:
В меню Сервис выберите команду Надстройки.
Нажмите кнопку Обзор, чтобы найти надстройку, которой нет в окне Список надстроек.
Установите в окне Список надстроек флажок той надстройки, которую необходимо загрузить, а затем нажмите кнопку OK.

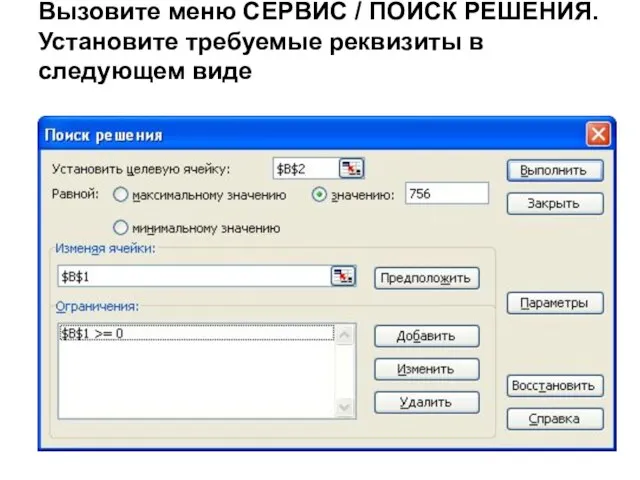
Вызовите меню СЕРВИС / ПОИСК РЕШЕНИЯ. Установите требуемые реквизиты в следующем виде

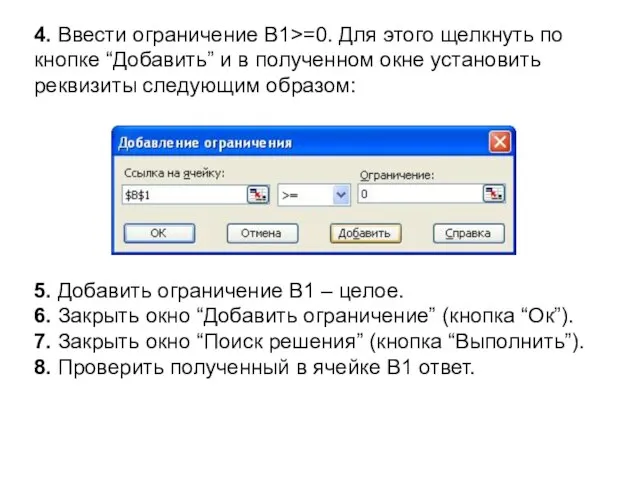
4. Ввести ограничение В1>=0. Для этого щелкнуть по кнопке “Добавить” и в полученном окне установить реквизиты следующим образом:
5. Добавить ограничение В1 – целое.
6. Закрыть окно “Добавить ограничение” (кнопка “Ок”).
7. Закрыть окно “Поиск решения” (кнопка “Выполнить”).
8. Проверить полученный в ячейке В1 ответ.

Оптимизационное моделирование
Используется в сфере управления сложными системами в экономике, когда необходимо осуществить поиск наиболее оптимального пути развития системы
Оптимальное развитие соответствует экстремальному значению выбранного целевого параметра
K = F(X1, X2, …, XN),
где К – значение целевого параметра, Х1…ХN - параметры

Цель исследования:
Найти экстремум функции (MAX, MIN), если функция нелинейная.
Определить ограничения на параметры, если целевая функция линейная.

Пример 2. Оптимальный план выпуска продукции
Фирма выпускает прогулочные и спортивные велосипеды. Ежемесячно сборочный цех способен собрать не более 600 прогулочных и не более 300 спортивных велосипедов. Качество каждого велосипеда проверяется на двух стендах А и В. Каждый прогулочный велосипед проверяется 0,3 ч. на стенде А и 0,1 ч. – на стенде В, а каждый спортивный велосипед проверяется 0,4 ч. на стенде А и 0,3 ч. – на стенде В. По технологическим причинам стенд А не может работать более 240 ч. в месяц, а стенд В – более 120 ч. в месяц. Реализация каждого прогулочного велосипеда приносит фирме доход в 50 руб., а каждого спортивного – 90 руб. Сколько прогулочных и сколько спортивных велосипедов должна ежемесячно выпускать фирма, чтобы ее прибыль была наибольшей?

Постановка задачи
Цель моделирования — составить такой производственный план, который обеспечит максимальную прибыль.
Объект моделирования — процесс производства и реализации велосипедов
Разработка модели
Исходные данные:
x - количество прогулочных велосипедов, выпускаемых ежемесячно фирмой;
y - количество спортивных велосипедов.
Занятость стенда А составляет 0,3х + 0,4y, что не должно превышать 240 ч.
Занятость стенда В составляет 0,1х + 0,3y, что не должно превышать 120 ч.
Прибыль фирмы составляет S = 50х + 90у (руб.)
Итак, мы пришли к следующей модели: необходимо найти целые значения х и у, удовлетворяющие системе неравенств
0,3х + 0,4y ≤ 240 О1
0,1х + 0,3y ≤ 120 О2
0 ≤ x ≤ 600 О3
0 ≤ y ≤ 300 О4
и такие, чтобы прибыль S = 50х + 90у была наибольшей.

Электронная таблица в режиме отображения формул

Компьютерный эксперимент
В среде электронных таблиц существует возможность автоматического поиска максимального (минимального) значения функции. Для этого:
Введите значения исходных данных в ячейки В3 и В4 – любые целые числа, учитывая ограничения О3 и О4;
Выберите команду [Сервис-Поиск решения...];
В появившемся диалоговом окне введите адрес ячейки, где содержится формула (функция для оптимизации);
Укажите цель оптимизации (максимальное значение);
Введите диапазон ячеек, посредством изменения значений которых будет достигнуто оптимальное значение целевой функции;
Введите все ограничения.

Вид таблицы Excel

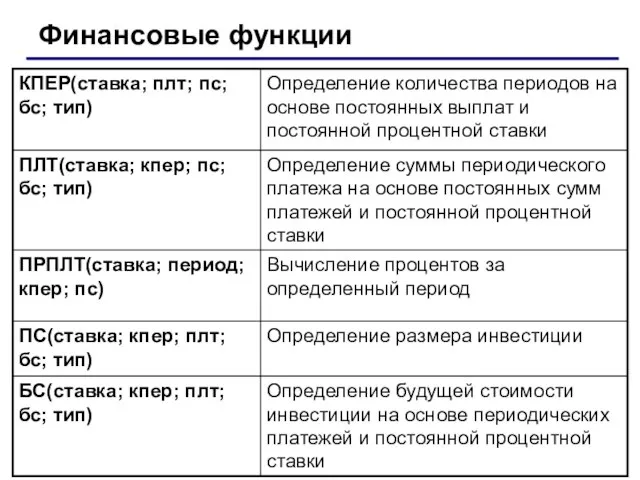
Финансовые функции

Аргументы функции ПЛТ
Ставка – процентная ставка по ссуде.
Кпер – общее число выплат по ссуде.
Пс – приведенная к текущему моменту стоимость, или общая сумма, которая на текущий момент равноценна ряду будущих платежей, называемая также основной суммой.
Бс – требуемое значение будущей стоимости, или остатка средств после последней выплаты. Если аргумент бс опущен, то он полагается равным 0 (нулю), т. е. для займа, например, значение Бс равно 0.
Тип – число 0 (нуль) или 1, обозначающее, когда должна производиться выплата – в конце периода (0) или в начале периода (1) .