The Capital Asset Pricing Model

CAPM впервые предложил У.Шарп
В России эту модель также называют МОДА (модель оценки долгосрочных активов)
CAPM позволяет точно прогнозировать взаимосвязь между риском какого-либо финансового актива и его ожидаемой доходностью.

Допущения в модели CAPM
Инвесторы не могут влиять на цены в результате сделок
Все инвесторы находятся в одинаковых условиях
Инвесторы не платят налогов на получаемые ими доходы и не несут операционных издержек при торговле ценными бумагами
Поведение инвесторов рационально

Основные финансовые понятия
Ожидаемая прибыль от вложений
r = (p1 + d - p0) / p0
Риск – распределение ожидаемой прибыли
Премия за риск
j = rj – rf
Предельная прибыль
Предельная прибыль k = δrp / δwk = rk
Предельная дисперсия
Предельная дисперсия k = δσp2 / δwk = 2∑wiσik = 2σkp
! Большинство инвесторов желают получить более высокие прибыли, при этом не расположены к риску.

Диверсификация как способ снижения риска
a) при n=2
rp = r1w1 + r2w2
σp2 = w12σ12 + w22σ22 + 2w1w2σ12 =
= σp2 = w12σ12 + w22σ22 + 2 w1w2p12σ1σ2 , т.к.
σ12 = p12σ1σ2
b) при n > 2

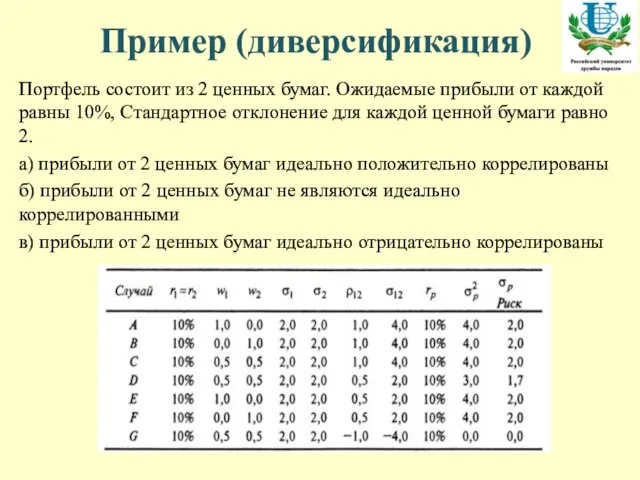
Пример (диверсификация)
Портфель состоит из 2 ценных бумаг. Ожидаемые прибыли от каждой равны 10%, Стандартное отклонение для каждой ценной бумаги равно 2.
а) прибыли от 2 ценных бумаг идеально положительно коррелированы
б) прибыли от 2 ценных бумаг не являются идеально коррелированными
в) прибыли от 2 ценных бумаг идеально отрицательно коррелированы

β- коэффициент
Чувствительность доходности ценной бумаги к изменениям доходности всего рынка
βk = σkp / σp2
Предельная дисперсия k = 2δσp2βk
Принцип оптимальности портфеля ценных бумаг
Оптимальным является портфель ценных бумаг, в котором все ценные бумаги с той же самой предельной дисперсией (или β-значением) должны иметь идентичные ожидаемые прибыли

Линейная зависимость между риском и прибылью
rp = (1-wa) rf + wara
σp2 = wa2σa2 + (1-wa)2σf2 + 2wa(1-wa)σaf , т.к.
σf2 = σaf = 0 , то σp2 = wa2σa2 или σp = waσa
Перегруппируем второе выражение и подставим в уравнение ожидаемой прибыли портфеля
rp = rf + ((ra- rf) / σa ) σp

Эконометрическая реализация структуры модели
Линейная зависимость для можели CAPM
rj - rf = (σj / σm) (rm - rf)
Первый множитель представляет собой βj
2. Обобщим уравнение путем добавления к нему постоянного члена αj и случайного возмущения εj
3. Уравнение оценки:
rj - rf = αj + βj(rm - rf) + εj

Применение CAPM
Управление инвестициями (сравнение ожидаемой доходности с объективной доходностью)
Планирование долгосрочных инвестиций (вычисление IRR)
Критика CAPM
Невозможно сформировать портфель, включающий абсолютно все активы
Не существует безрисковой ставки
критика предпосылки об идеальных инвесторах
На ожидаемую доходность влияет не только систематический риск