Содержание
- 2. Для каждого из событий определите, каким оно является – невозможным, достоверным или случайным: а) из 25
- 3. Типы событий || Противоположное событие (по отношению к рассматриваемому событию А) – это событие , которое
- 4. Примеры противоположных событий: если сейчас день, то сейчас не ночь; если человек спит, то в данный
- 5. Задание 1 Назовите событие противоположное данному: при бросании монеты выпала решка; Алеша вытащил выигрышный билет в
- 6. Типы событий || Два события А и В называют совместными, если они могут произойти одновременно, при
- 7. Примеры совместных и несовместных событий: совместные события: идет дождь и идет снег, человек ест и человек
- 8. Задание 2 Укажите совместность – несовместность случайных событий: а) (Катя со Славой играли в шахматы) А
- 9. Действия над событиями 1. Суммой нескольких событий называется событие, состоящие в наступлении хотя бы одного из
- 10. Действия над событиями Пример. В урне находятся красные, белые и черные шары. Вынимается один шар. Возможные
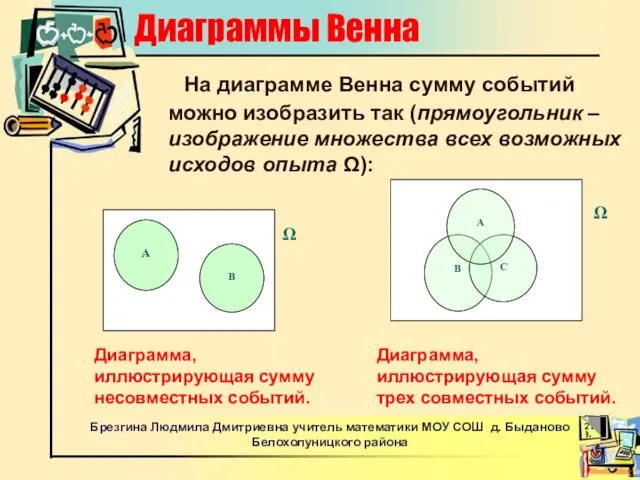
- 11. Диаграммы Венна На диаграмме Венна сумму событий можно изобразить так (прямоугольник – изображение множества всех возможных
- 12. Примеры суммы событий: пусть А - идет дождь, а В - идет снег, то (А +
- 13. Действия над событиями 2. Произведением нескольких событий называется событие, состоящие в совместном наступлении всех этих событий
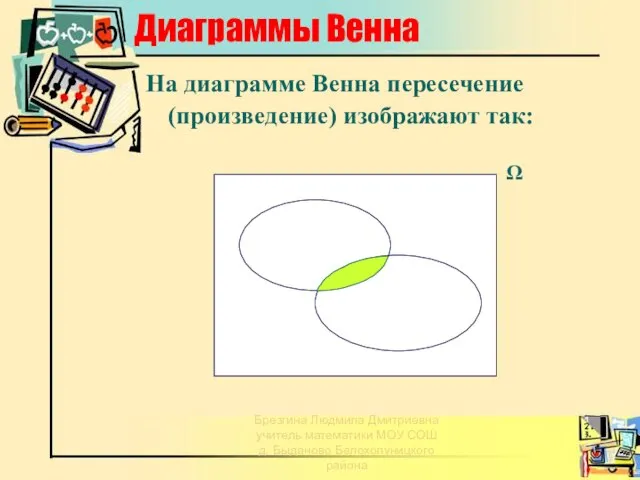
- 14. Диаграммы Венна На диаграмме Венна пересечение (произведение) изображают так: Ω Брезгина Людмила Дмитриевна учитель математики МОУ
- 15. Примеры произведения событий: Пусть А - из урны вытянули белый шар, В - из урны вытянули
- 16. Задание 3 Опишите, в чем состоит сумма следующих несовместных событий. А – учитель вызвал к доске
- 17. Диаграммы Венна Графические изображения на плоскости соотношений между множествами называются диаграммами Венна. Брезгина Людмила Дмитриевна учитель
- 18. Дополнительные задания Задание 4. Из событий: 1) «наступило утро»; 2) «сегодня по расписанию шесть уроков»; 3)
- 19. Вопросы Могут ли события быть одновременно и несовместными и совместными? Входит ли в понятие суммы событий
- 21. Скачать презентацию
















 Стипендия Правительства области
Стипендия Правительства области المالية االستدامة المالية
المالية االستدامة المالية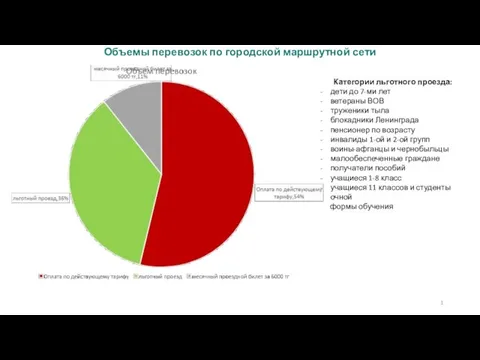 Объемы перевозок по городской маршрутной сети
Объемы перевозок по городской маршрутной сети День инвалида
День инвалида Презентация на тему Интернет и его возможности
Презентация на тему Интернет и его возможности Extenzionálne modely. Algebraická teória. Transformácie intervalov. Definícia funkcie Glob. (Téma 5)
Extenzionálne modely. Algebraická teória. Transformácie intervalov. Definícia funkcie Glob. (Téma 5) Культура Древней Греции
Культура Древней Греции Штриховая гладь
Штриховая гладь Профессия Повар-кондитер
Профессия Повар-кондитер Организационное стимулирование. Условия для внедрения мотивации персонала
Организационное стимулирование. Условия для внедрения мотивации персонала Что такое бенилюкс?
Что такое бенилюкс? Презентация на тему Здоровьесберегающие технологии на уроках в начальной школе. Окружающий мир 3 класс
Презентация на тему Здоровьесберегающие технологии на уроках в начальной школе. Окружающий мир 3 класс  FOOD SAFETY
FOOD SAFETY  Ассирия
Ассирия Презентация на тему Кометы и метеоры
Презентация на тему Кометы и метеоры Руководство Ernst&Young по составления бизнес-планов
Руководство Ernst&Young по составления бизнес-планов Куклы из махровых носков
Куклы из махровых носков Конституционные суды Приволжского Федерального округа
Конституционные суды Приволжского Федерального округа Японская каллиграфия - диалог культур Токио - Красноярск
Японская каллиграфия - диалог культур Токио - Красноярск «Пилот»: Маркетинг в компании
«Пилот»: Маркетинг в компании Устный журнал. В мире имён и названий
Устный журнал. В мире имён и названий Баскетбол. Тест по физической культуре
Баскетбол. Тест по физической культуре Материаловедение 5-6р
Материаловедение 5-6р Применение приборов серии IVS для решения задач вибродиагностики
Применение приборов серии IVS для решения задач вибродиагностики Композиционное решение для предприятий автомобилестроительной отрасли на основе системы MFG/PRO
Композиционное решение для предприятий автомобилестроительной отрасли на основе системы MFG/PRO Никола Тесла-повелитель молний
Никола Тесла-повелитель молний Проверка понимания озвученного текста
Проверка понимания озвученного текста Представление графической информации в компьютере
Представление графической информации в компьютере