Содержание
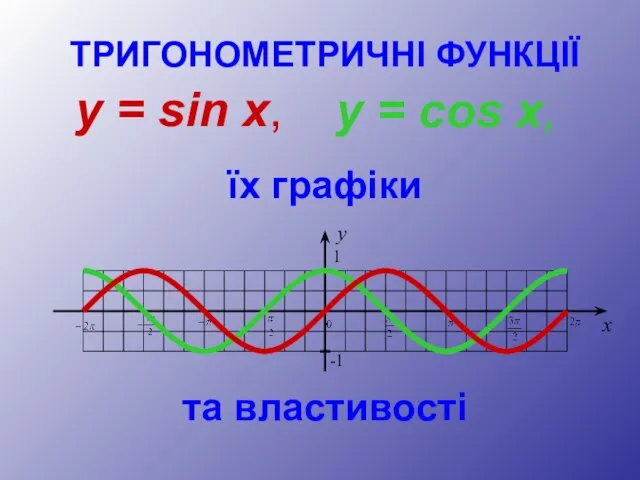
- 2. ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ y = sin x, y = cos x, їх графіки та властивості y 1
- 3. Синус (від лат. sinus) – вигин, кривизна.
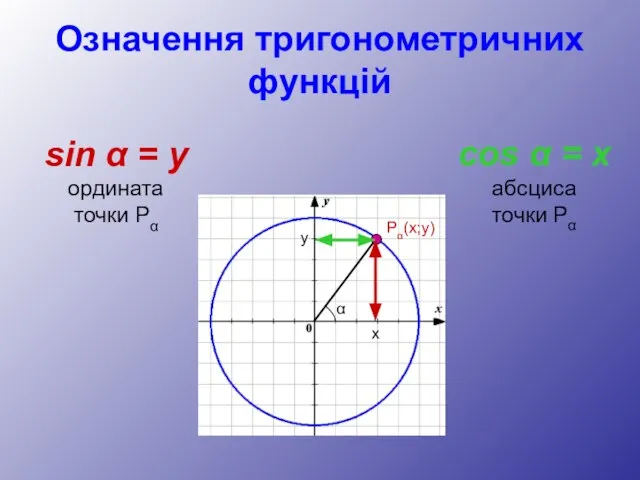
- 4. Означення тригонометричних функцій sin α = y ордината точки Pα cos α = x абсциса точки
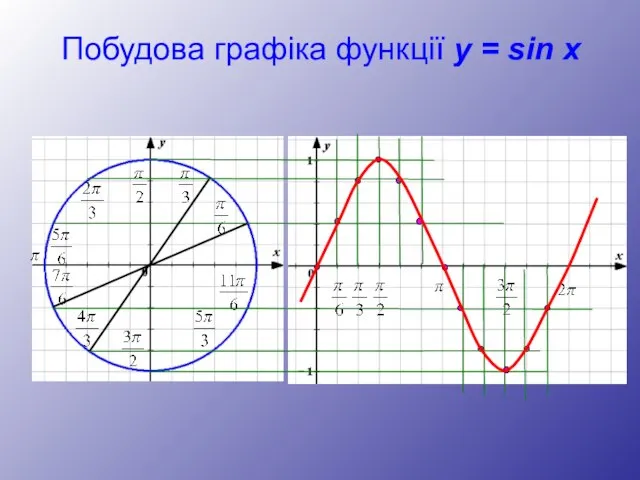
- 5. Побудова графіка функції y = sin x
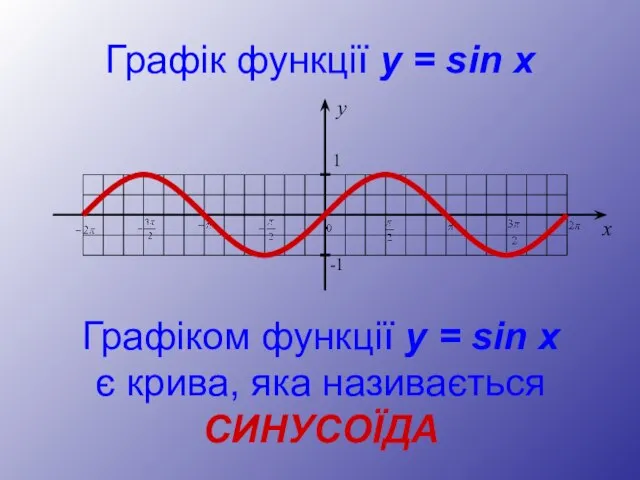
- 6. Графік функції y = sin x Графіком функції y = sin x є крива, яка називається
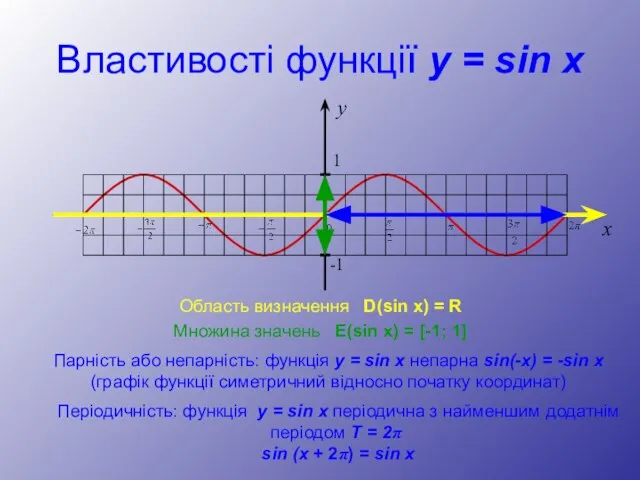
- 7. Властивості функції y = sin x Область визначення D(sin x) = R Множина значень E(sin x)
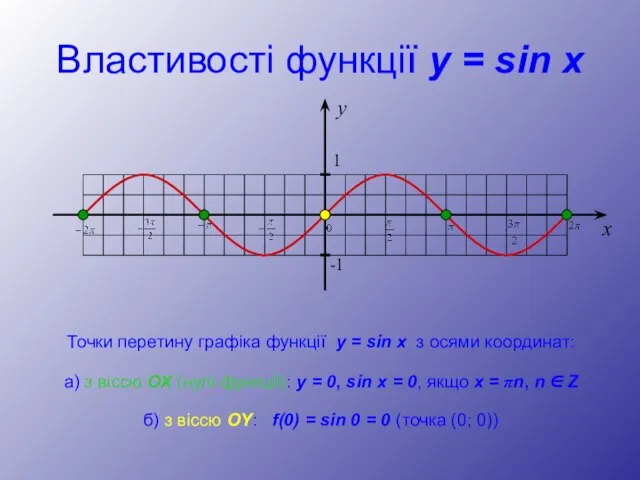
- 8. Властивості функції y = sin x Точки перетину графіка функції y = sin x з осями
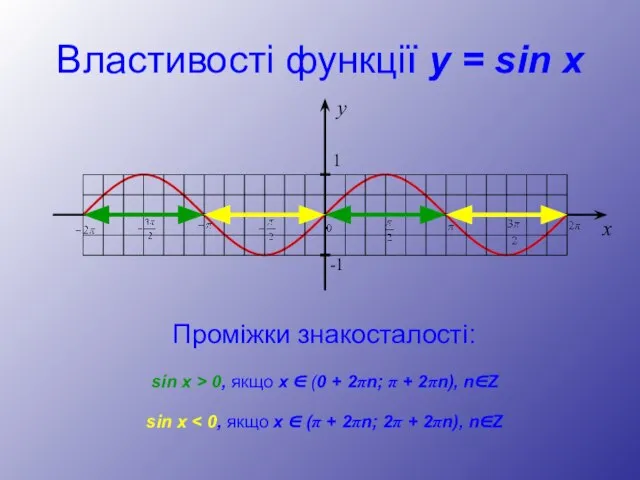
- 9. Властивості функції y = sin x Проміжки знакосталості: sin x > 0, якщо х ∈ (0
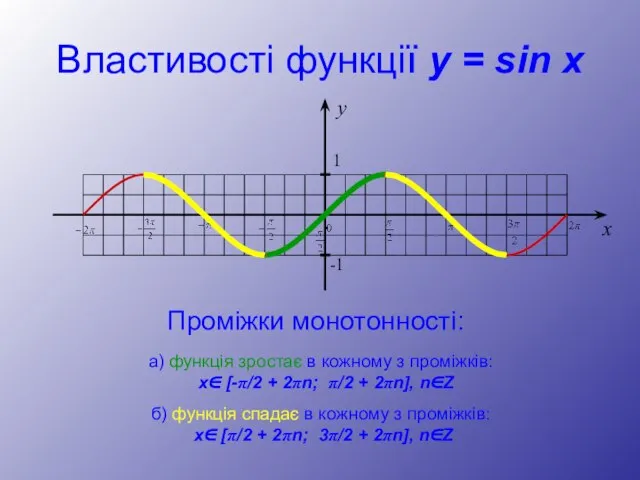
- 10. Властивості функції y = sin x Проміжки монотонності: а) функція зростає в кожному з проміжків: x∈
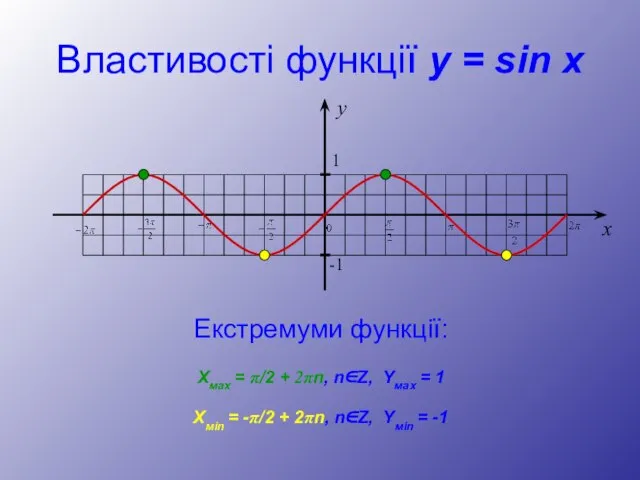
- 11. Властивості функції y = sin x Екстремуми функції: Хмах = π/2 + 2πn, n∈Z, Yмах =
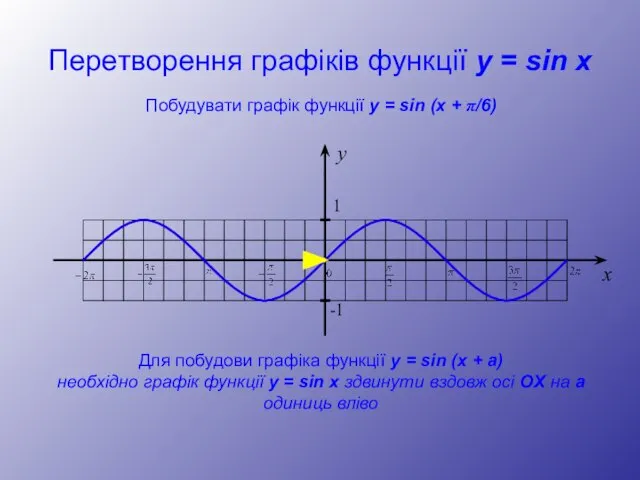
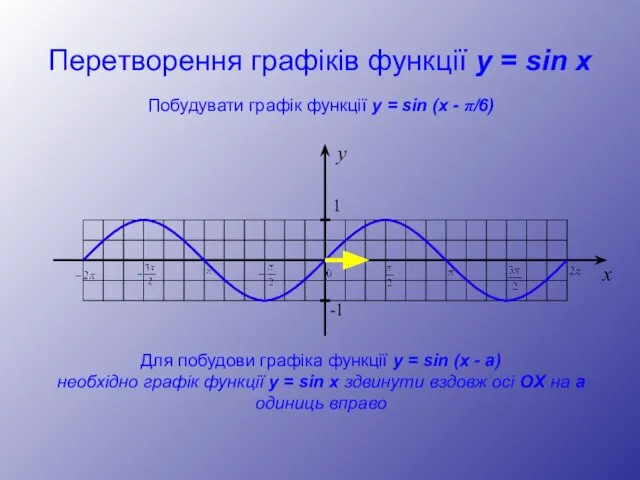
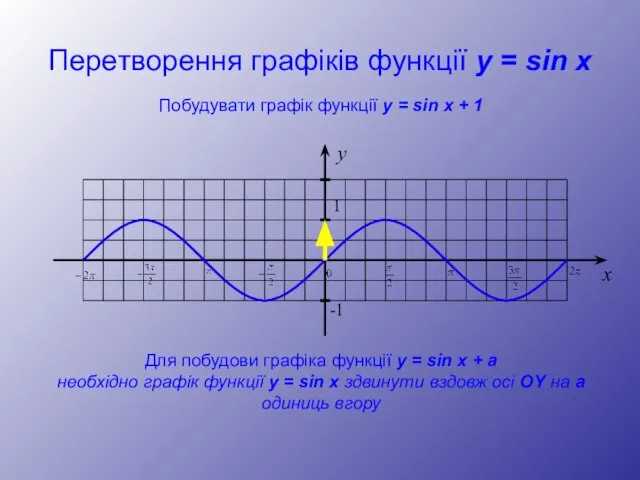
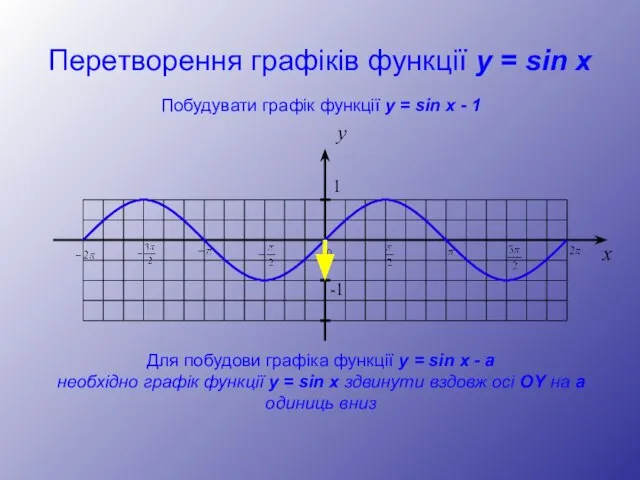
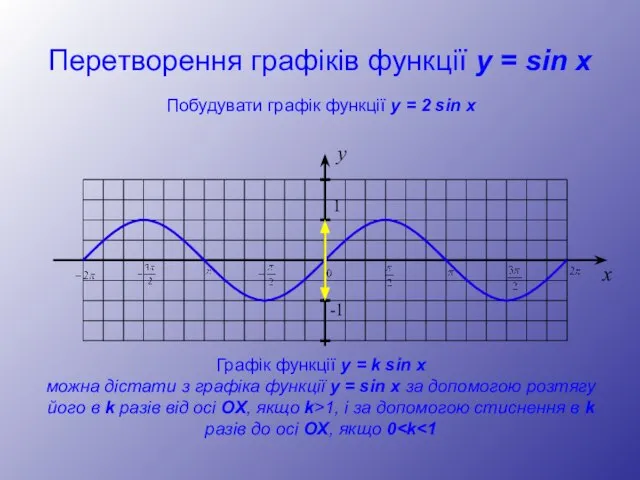
- 12. Перетворення графіків функції y = sin x y 1 -1 x Побудувати графік функції y =
- 13. Перетворення графіків функції y = sin x y 1 -1 x Побудувати графік функції y =
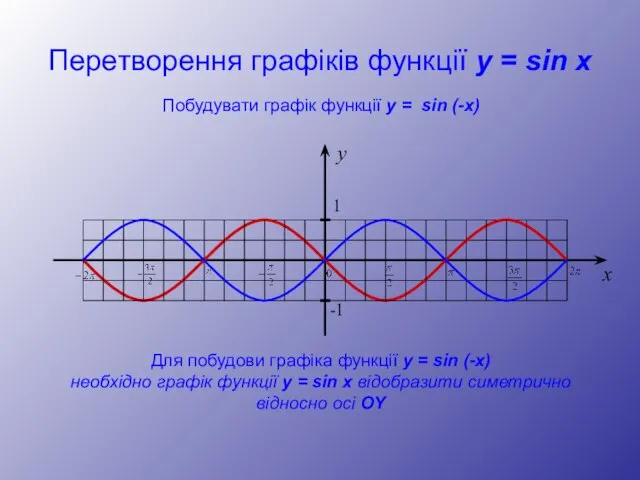
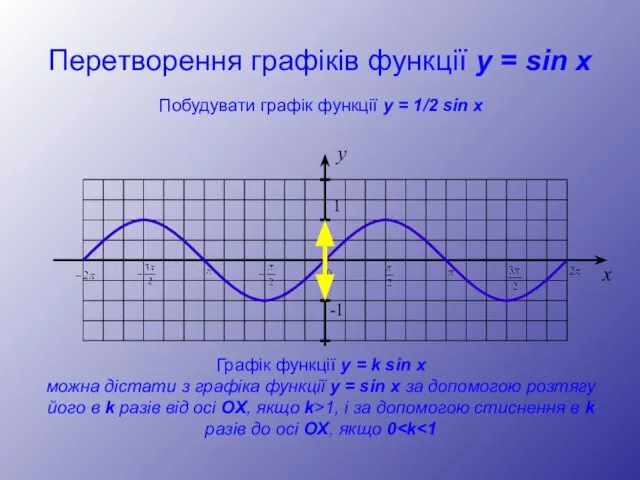
- 14. Перетворення графіків функції y = sin x y 1 -1 x Побудувати графік функції y =
- 15. Перетворення графіків функції y = sin x y 1 -1 x Побудувати графік функції y =
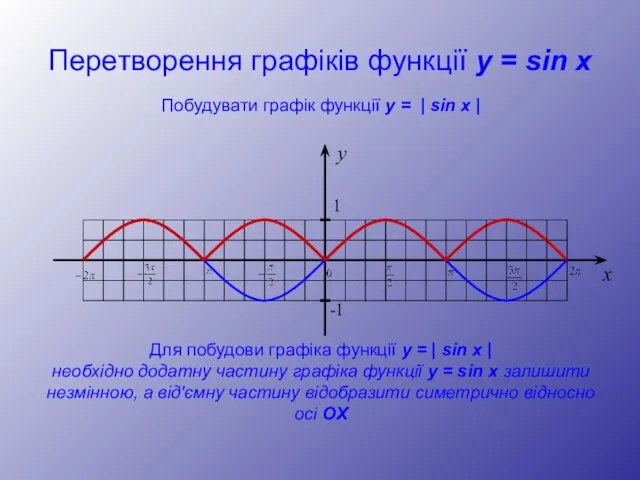
- 16. Перетворення графіків функції y = sin x y 1 -1 x Побудувати графік функції y =
- 17. Перетворення графіків функції y = sin x y 1 -1 x Побудувати графік функції y =
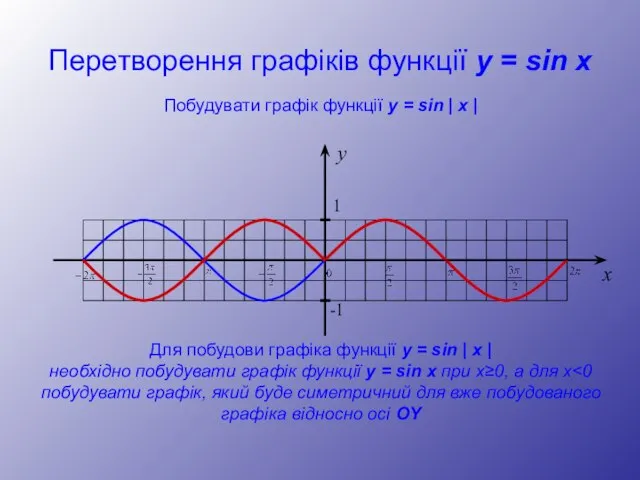
- 18. Перетворення графіків функції y = sin x y 1 -1 x Побудувати графік функції y =
- 19. Перетворення графіків функції y = sin x y 1 -1 x Побудувати графік функції y =
- 20. Перетворення графіків функції y = sin x y 1 -1 x Побудувати графік функції y =
- 21. Перетворення графіків функції y = sin x y 1 -1 x Побудувати графік функції y =
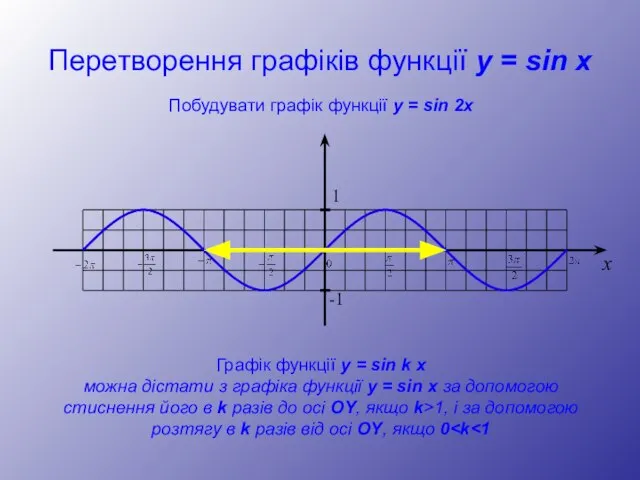
- 22. Перетворення графіків функції y = sin x Побудувати графік функції y = sin 2x Графік функції
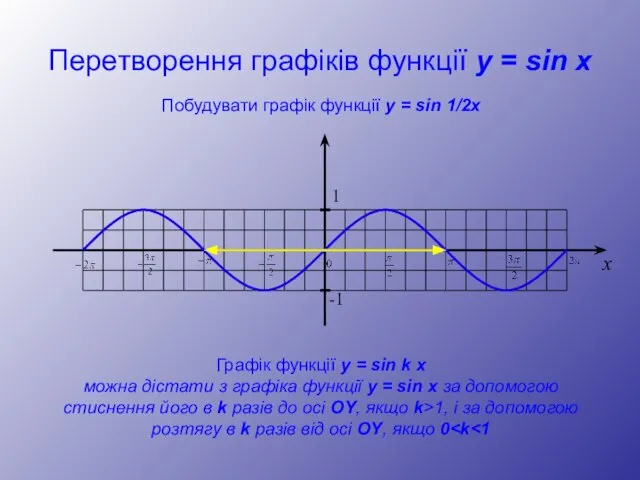
- 23. Перетворення графіків функції y = sin x Побудувати графік функції y = sin 1/2x Графік функції
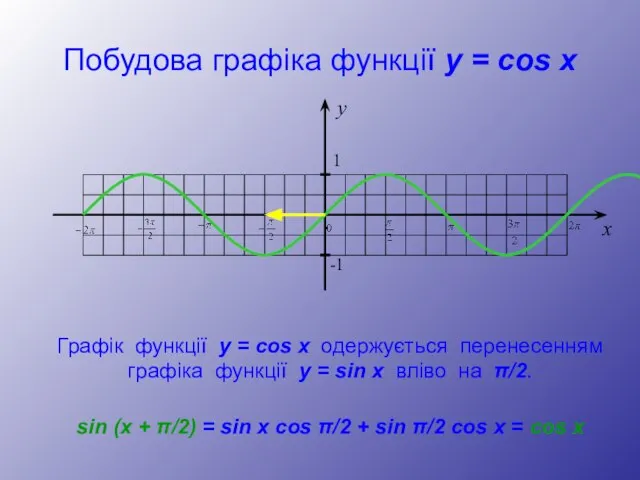
- 24. Побудова графіка функції y = cos x Графік функції у = cos x одержується перенесенням графіка
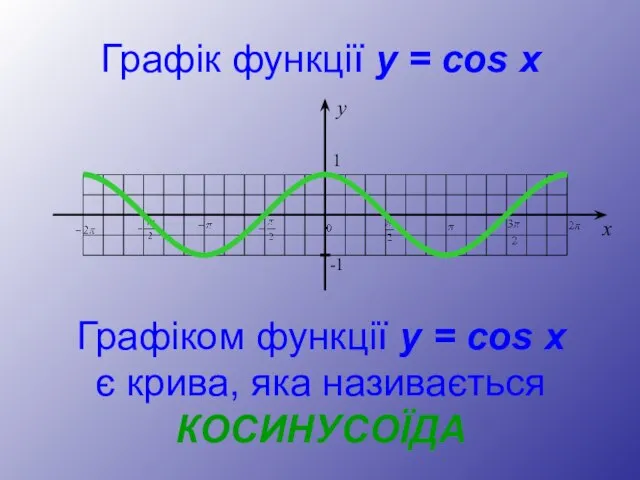
- 25. Графік функції y = cos x Графіком функції y = cos x є крива, яка називається
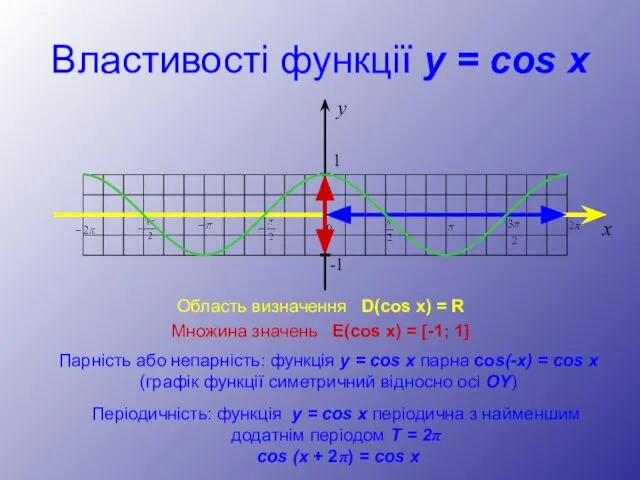
- 26. Властивості функції y = cos x Область визначення D(cos x) = R Множина значень E(cos x)
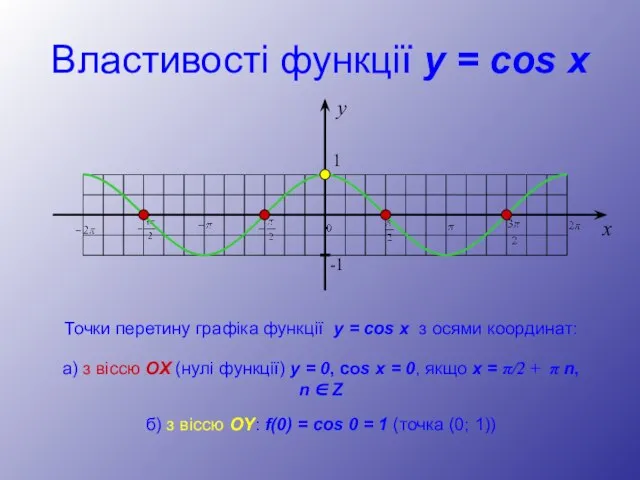
- 27. Точки перетину графіка функції y = cos x з осями координат: Властивості функції y = cos
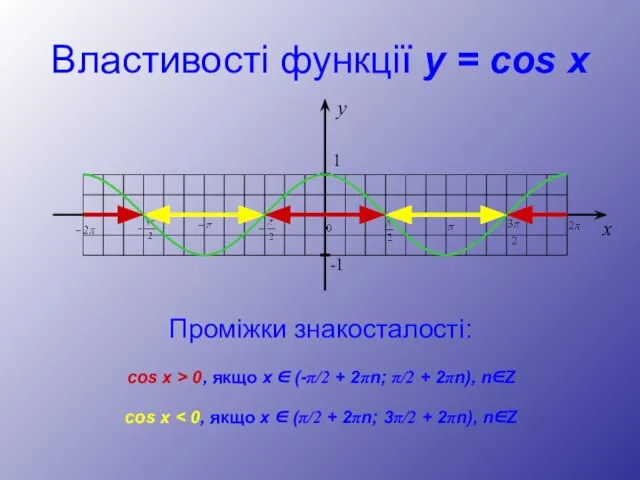
- 28. Властивості функції y = cos x Проміжки знакосталості: cos x > 0, якщо х ∈ (-π/2
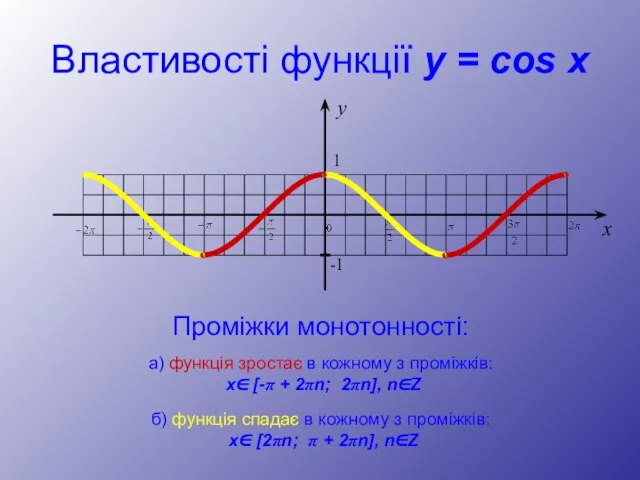
- 29. Властивості функції y = cos x Проміжки монотонності: б) функція спадає в кожному з проміжків: x∈
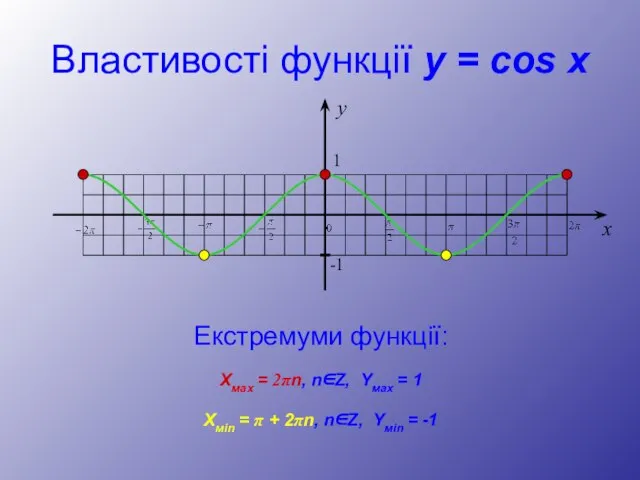
- 30. Властивості функції y = cos x Екстремуми функції: Хмах = 2πn, n∈Z, Yмах = 1 Хмin
- 31. Перетворення графіків функції y = cos x Перетворення графіків функції y = cos x відбувається аналогічно
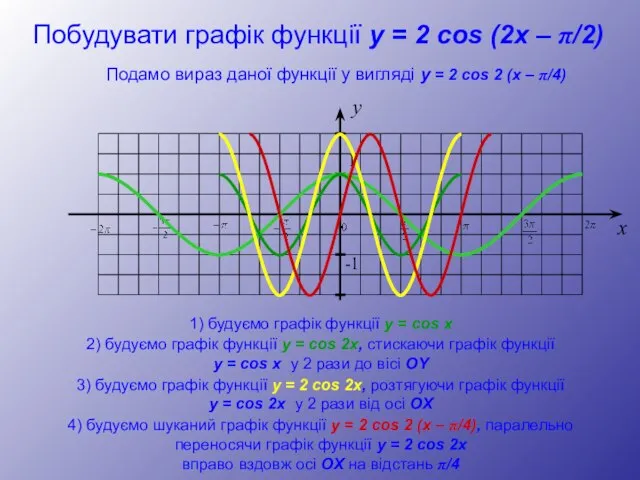
- 32. y 1 -1 x Побудувати графік функції y = 2 cos (2x – π/2) 1) будуємо
- 33. Практичне застосування тригонометричних функцій Синусоїда – хвилеподібна плоска крива, яка є графіком тригонометричної функції y =
- 35. Скачать презентацию




 Презентация на тему Макроэволюция
Презентация на тему Макроэволюция Акробатические упражнения
Акробатические упражнения Лицо – природы дар и гордость человека и наше эмоциональное состояние написано на лице.
Лицо – природы дар и гордость человека и наше эмоциональное состояние написано на лице. О ходе реализации ФЦП
О ходе реализации ФЦП Типичный американский дом
Типичный американский дом Машинное обучение: качество
Машинное обучение: качество ДИСЛАЛИЯ
ДИСЛАЛИЯ Нормы группы (правила работы)
Нормы группы (правила работы) Продукты Кэшбери
Продукты Кэшбери Готовимся к ГИА (А2, В11,В12)
Готовимся к ГИА (А2, В11,В12) Творчество В.Ф. Тендрякова
Творчество В.Ф. Тендрякова Областной проект развития детского туризма Открывай Курский край
Областной проект развития детского туризма Открывай Курский край «Опыт организации взаимодействия российских научных организаций и промышленных компаний, работающих в сфере биотехнологии» Бел
«Опыт организации взаимодействия российских научных организаций и промышленных компаний, работающих в сфере биотехнологии» Бел Мотивация обучающихся в онлайн. Психологические приемы
Мотивация обучающихся в онлайн. Психологические приемы ООО «Управляющая компания №1»
ООО «Управляющая компания №1» Директора школы
Директора школы Кодирование графической информации
Кодирование графической информации Загадки для детей младшего дошкольного возраста
Загадки для детей младшего дошкольного возраста Особенности работы с объемными объектами дизайна
Особенности работы с объемными объектами дизайна Образ человека, характер одежды в японской культуре
Образ человека, характер одежды в японской культуре Туризм в России: каталог святынь Красногвардейского района Белгородской области
Туризм в России: каталог святынь Красногвардейского района Белгородской области Создание композиции с учетом технических и композиционных особенностей книжной графики
Создание композиции с учетом технических и композиционных особенностей книжной графики Сравнение чисел. Числовые неравенства
Сравнение чисел. Числовые неравенства УРОК №5 ПРЕДЕЛЬНЫЕ УГЛЕВОДОРОДЫ (АЛКАНЫ)
УРОК №5 ПРЕДЕЛЬНЫЕ УГЛЕВОДОРОДЫ (АЛКАНЫ) Основные элементы проектной деятельности
Основные элементы проектной деятельности НРАВЫ МУСУЛЬМАНИНА
НРАВЫ МУСУЛЬМАНИНА Публичный отчет МОУ«СОШ № 45 г.Чебоксары»
Публичный отчет МОУ«СОШ № 45 г.Чебоксары» Способы подачи блюд из мяса
Способы подачи блюд из мяса