Содержание
- 2. Верно ли, что:
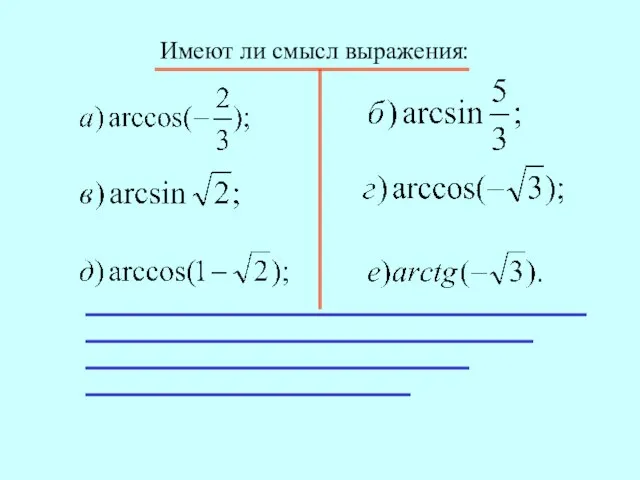
- 3. Имеют ли смысл выражения:
- 4. Решить уравнение:
- 5. Пример 1. Решить уравнение 2 sin2x + sinx - 1 = 0. Решение. Введём новую переменную
- 6. 1) sinx = 1/2, 2) sinx = -1,
- 7. Решение. Заменяя sin2x на 1-сos2x, получим квадратное уравнение относительно сosx. 6 ( 1-cos2x ) + 5
- 8. Cледовательно, сos x = - 1/2 или cos x = 4/3. Уравнение cos x = 4/3
- 9. Пример 3. Решить уравнение tgx + 2ctgx = 3. то уравнение можно записать в виде: Обозначим
- 10. t2 - 3t + 2 = 0. По теореме, обратной теореме Виета, t1 = 2, t2=1.
- 11. Пример 4. sin2 4x = 1/4 cos 2x =1/2 Решение. Х= ±π/6 + πn; n Є
- 13. Скачать презентацию



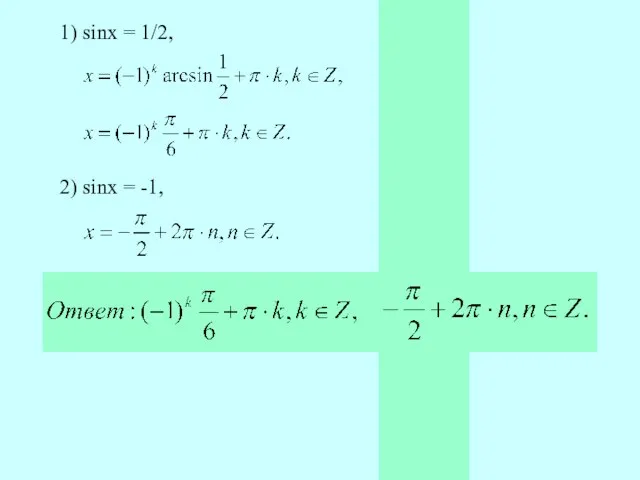





 Useless Inventions
Useless Inventions  Моделирование объектов и систем
Моделирование объектов и систем Личное благовестие
Личное благовестие Презентация на тему: Работа классного руководителя с родителями
Презентация на тему: Работа классного руководителя с родителями 2_5325994725348481395
2_5325994725348481395 Организация туриндустрии. Комплекс услуг предприятий питания и его роль в туризме
Организация туриндустрии. Комплекс услуг предприятий питания и его роль в туризме Организация внеурочной деятельности при реализации федерального государственного образовательного стандарта начального общего
Организация внеурочной деятельности при реализации федерального государственного образовательного стандарта начального общего Презентация на тему Формы взаимодействия педагогов с семьей ребенка дошкольного возраста с особыми образовательными потребностя
Презентация на тему Формы взаимодействия педагогов с семьей ребенка дошкольного возраста с особыми образовательными потребностя К вопросу о цикличности развития диатомовых водорослей Байкала
К вопросу о цикличности развития диатомовых водорослей Байкала О мерах, направленных на снижение темпов роста потребительских цен
О мерах, направленных на снижение темпов роста потребительских цен «Своя игра»
«Своя игра» ГУО Туринский учебно-педагогический комплекс детский сад – базовая школа
ГУО Туринский учебно-педагогический комплекс детский сад – базовая школа Презентация на тему Удельный период русской истории (6 класс)
Презентация на тему Удельный период русской истории (6 класс) Красная книга Курганской области
Красная книга Курганской области Презентация на тему have to - must
Презентация на тему have to - must Что такое ДМС страхование? Полис(пластиковый, эл. вариант, бумажный)
Что такое ДМС страхование? Полис(пластиковый, эл. вариант, бумажный) Производство бумаги
Производство бумаги СДД как инструмент хеджирования ценовых рисков в РСВ
СДД как инструмент хеджирования ценовых рисков в РСВ Конкурс курсовых проектов (КМИП)
Конкурс курсовых проектов (КМИП) Менеджмент. Организация, мотивации, контроль, понятие регулирования и его место в системе управления (Часть 3)
Менеджмент. Организация, мотивации, контроль, понятие регулирования и его место в системе управления (Часть 3) Лаборатория 812 – это содружество людей, абсолютно разных, но уже состоявшихся в своих профессиональных сферах. Художники, психолог
Лаборатория 812 – это содружество людей, абсолютно разных, но уже состоявшихся в своих профессиональных сферах. Художники, психолог Должность и прием персонала
Должность и прием персонала Возникновение головных уборов
Возникновение головных уборов Почва – важнейшая часть экосистемы 3 класс
Почва – важнейшая часть экосистемы 3 класс Свойства и функции белков
Свойства и функции белков  Самопрезентация учителя начальных классов
Самопрезентация учителя начальных классов Демонстрационный эксперимент по геометрической оптике
Демонстрационный эксперимент по геометрической оптике Презентация на тему Предложения с вводными конструкциями (8 класс)
Презентация на тему Предложения с вводными конструкциями (8 класс)