Циклические алгоритмы Решение типовых задач

ОСНОВНЫЕ ПОНЯТИЯ
Алгоритм циклической структуры предусматривает многократное повторение действий в одной и той же последовательности по одним и тем же математическим зависимостям, но при разных значениях специально изменяемой величины.

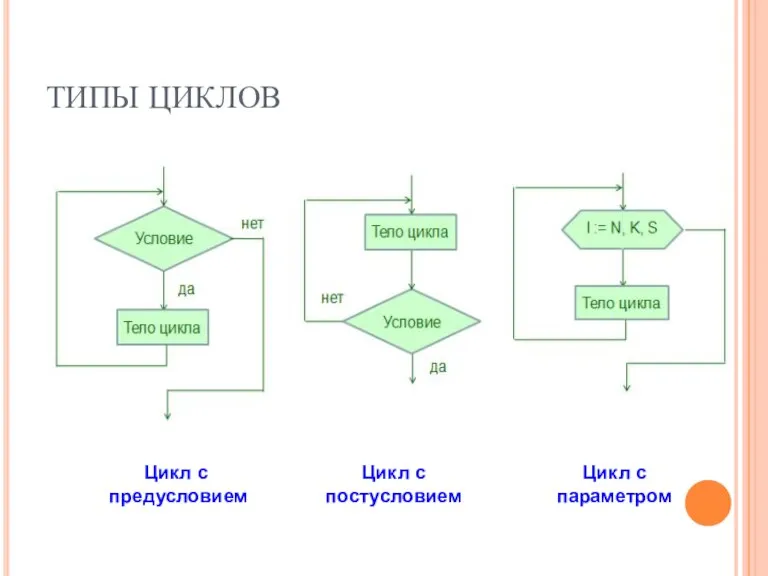
ТИПЫ ЦИКЛОВ
Цикл с
предусловием
Цикл с постусловием
Цикл с параметром

ТИПОВЫЕ ЗАДАЧИ
Вычисление суммы и произведения
Подсчет количества элементов
Табулирование функций
Нахождение наибольшего общего делителя (НОД) двух натуральных чисел
Нахождение количества делителей числа
Проверка числа на «простоту»
Проверить, является ли число палиндромом
Определение самой большой цифры натурального числа и ее позиции в этом числе

ВЫЧИСЛЕНИЕ СУММЫ И ПРОИЗВЕДЕНИЯ
Для построения алгоритма решения таких задач используется цикл с параметром, т. к. число шагов цикла известно.
При вычислении суммы и произведения используется прием накопления.

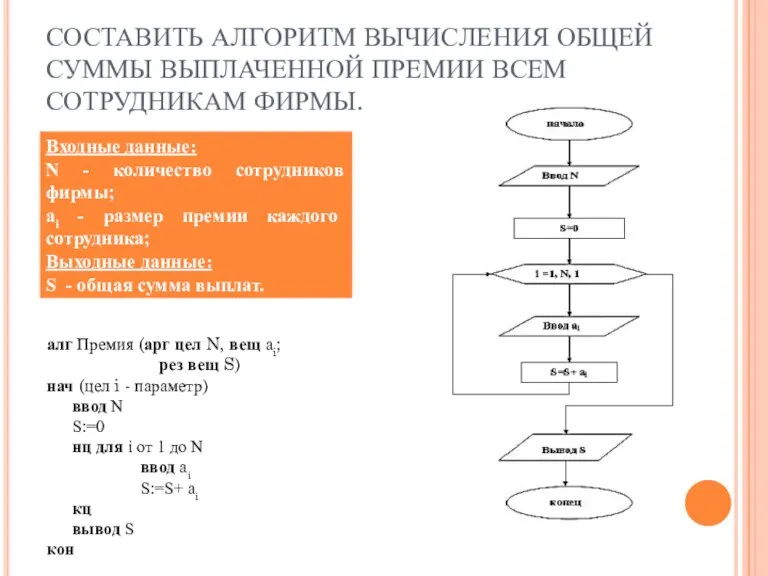
СОСТАВИТЬ АЛГОРИТМ ВЫЧИСЛЕНИЯ ОБЩЕЙ СУММЫ ВЫПЛАЧЕННОЙ ПРЕМИИ ВСЕМ СОТРУДНИКАМ ФИРМЫ.
алг Премия (арг цел N, вещ аi;
рез вещ S)
нач (цел i - параметр)
ввод N
S:=0
нц для i от 1 до N
ввод аi
S:=S+ аi
кц
вывод S
кон

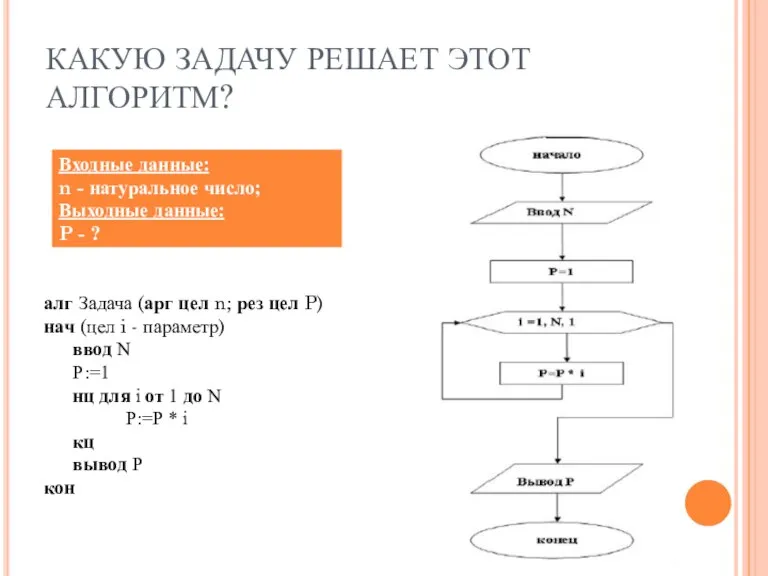
КАКУЮ ЗАДАЧУ РЕШАЕТ ЭТОТ АЛГОРИТМ?
алг Задача (арг цел n; рез цел P)
нач (цел i - параметр)
ввод N
Р:=1
нц для i от 1 до N
Р:=Р * i
кц
вывод Р
кон

ПОДСЧЕТ КОЛИЧЕСТВА ЭЛЕМЕНТОВ
Подсчет количества элементов сводится к вычислению количества натуральных чисел в последовательности 1, 2, 3, 4 и т. д.
Правило счетчика:
начальное значение счетчика К=0
в теле циклической конструкции выполняется команда
К = К+1
если не задано дополнительных условий,
где К – промежуточное значение счетчика.

СОСТАВИТЬ АЛГОРИТМ ПОДСЧЕТА КОЛИЧЕСТВА СОТРУДНИКОВ ФИРМЫ, ЗАРПЛАТА КОТОРЫХ ПРЕВЫШАЕТ 20 ТЫС. РУБ.
(Составить алгоритм подсчета количества чисел больших 20000 среди n заданных).
алг Сотрудники (арг цел n; вещ S;
рез цел K)
нач (цел i - параметр)
K:=0
нц для i от 1 до n
ввод S
если S>20000 то К:=К + 1
все
кц
вывод К
кон

ТАБУЛИРОВАНИЕ ФУНКЦИИ
Табулирование функции - это вычисление значений функции при изменении аргумента от некоторого начального значения до некоторого конечного значения с определенным шагом.
Алгоритм табулирования содержит все основные конструкции: линейную, ветвление, цикл. В общем виде алгоритм можно описать так:
1. Определяется переменная (обычно X);
2. Перед циклом задается начальное значение переменной, условием окончания цикла является достижение переменной конечного значения;
3. В теле цикла на каждом шаге вычисляется значение функции Y, зависящее от переменной X (формируется строка таблицы);
4. В конце каждого шага значение переменной изменяется на h, где h - заданный шаг изменения, т. е. X = X + h.

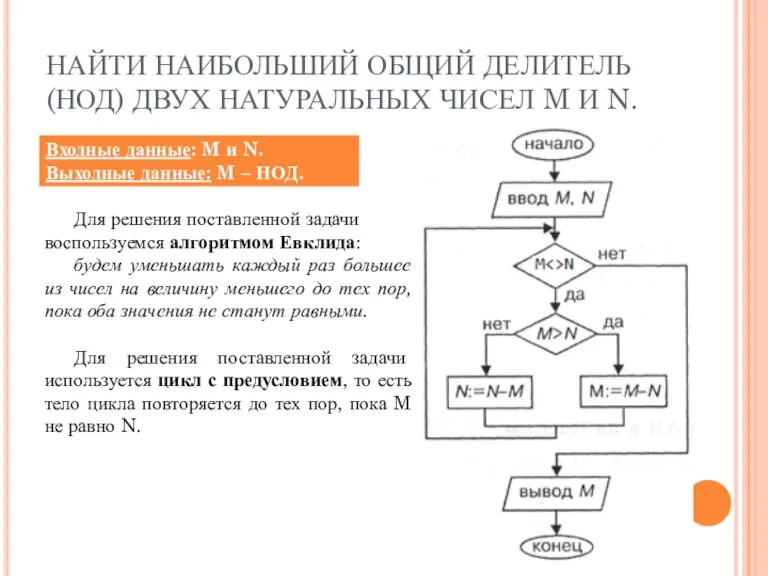
НАЙТИ НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ (НОД) ДВУХ НАТУРАЛЬНЫХ ЧИСЕЛ M И N.
Для решения поставленной задачи воспользуемся алгоритмом Евклида:
будем уменьшать каждый раз большее из чисел на величину меньшего до тех пор, пока оба значения не станут равными.
Для решения поставленной задачи используется цикл с предусловием, то есть тело цикла повторяется до тех пор, пока M не равно N.

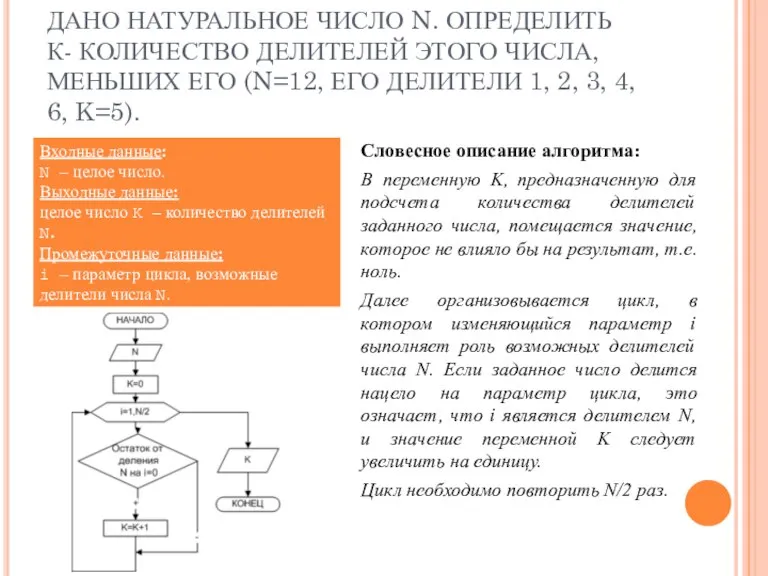
ДАНО НАТУРАЛЬНОЕ ЧИСЛО N. ОПРЕДЕЛИТЬ
К- КОЛИЧЕСТВО ДЕЛИТЕЛЕЙ ЭТОГО ЧИСЛА, МЕНЬШИХ ЕГО (N=12, ЕГО ДЕЛИТЕЛИ 1, 2, 3, 4, 6, K=5).
Словесное описание алгоритма:
В переменную K, предназначенную для подсчета количества делителей заданного числа, помещается значение, которое не влияло бы на результат, т.е. ноль.
Далее организовывается цикл, в котором изменяющийся параметр i выполняет роль возможных делителей числа N. Если заданное число делится нацело на параметр цикла, это означает, что i является делителем N, и значение переменной K следует увеличить на единицу.
Цикл необходимо повторить N/2 раз.

ДАНО НАТУРАЛЬНОЕ ЧИСЛО N. ОПРЕДЕЛИТЬ, ЯВЛЯЕТСЯ ЛИ ОНО ПРОСТЫМ.
Натуральное число N называется простым, если оно делится нацело без остатка только на единицу и N.
Словесное описание алгоритма:
Инициализировать значение логической переменной flag;
Определить значение делителя для числа N;
Организовать цикл с предусловием, который будет выполняться до тех пор, пока либо будет найден хотя бы один делитель (тогда flag примет значение ложь), либо до середины числа N
алг Простое_число (арг цел N; рез утв)
нач (цел delit, лог flag)
ввод N
flag := истина
delit := 2
пока (flag и (delit < div(N, 2)))
нц
если mod(N, delit) = 0 то flag := ложь
иначе delit := delit + 1
все
кц
если flag то вывод («Введенное число простое»)
иначе вывод («Введенное число составное»)
все
кон

ПРОВЕРИТЬ, ЯВЛЯЕТСЯ ЛИ ЧИСЛО …
алг Число (арг цел N; рез утв)
нач (цел a, цел b)
ввод N
a := N
b := 0
пока (a<>0)
нц
b := b*10+a mod 10
a := a div 10
кц
если N=b то вывод («Введенное число …»)
иначе вывод («Введенное число не является …»)
все
кон
Составьте словесное описание алгоритма

ДАНО НАТУРАЛЬНОЕ ЧИСЛО N. ОПРЕДЕЛИТЬ САМУЮ БОЛЬШУЮ ЦИФРУ И ЕЕ ПОЗИЦИЮ В ЧИСЛЕ
N=573863, наибольшей является цифра 8, ее позиция – четвертая слева

ДАНО НАТУРАЛЬНОЕ ЧИСЛО N. ОПРЕДЕЛИТЬ САМУЮ БОЛЬШУЮ ЦИФРУ И ЕЕ ПОЗИЦИЮ В ЧИСЛЕ
Разобьем решение этой задачи на два этапа.
Вначале найдем количество цифр в заданном числе.
Определим наибольшую цифру и ее позицию.

ДАНО НАТУРАЛЬНОЕ ЧИСЛО N. ОПРЕДЕЛИТЬ САМУЮ БОЛЬШУЮ ЦИФРУ И ЕЕ ПОЗИЦИЮ В ЧИСЛЕ
Для того, чтобы подсчитать количество цифр в числе, необходимо:
определить, сколько раз заданное число можно разделить на десять нацело.
Например, пусть N=12345, тогда количество цифр kol = 5. Результаты вычислений сведены в таблице 1:

ДАНО НАТУРАЛЬНОЕ ЧИСЛО N. ОПРЕДЕЛИТЬ САМУЮ БОЛЬШУЮ ЦИФРУ И ЕЕ ПОЗИЦИЮ В ЧИСЛЕ
Процесс определения текущей цифры числа N=12345 представлен в таблице 2:

ДАНО НАТУРАЛЬНОЕ ЧИСЛО N. ОПРЕДЕЛИТЬ САМУЮ БОЛЬШУЮ ЦИФРУ И ЕЕ ПОЗИЦИЮ В ЧИСЛЕ
Алгоритм поиска максимального значения в некоторой последовательности цифр заключается в следующем.
В ячейку, в которой будет храниться максимальный элемент (max), записывают значение, меньшее любого из элементов последовательности (в нашем случае max=-1, так как цифры числа находятся в диапазоне от 0 до 9).
Затем сравнивают элементы последовательности со значением ячейки max. Если найдется элемент, превышающий значение предполагаемого максимума, то ячейке max необходимо присвоить значение этого элемента и, соответственно, запомнить его номер в последовательности (в нашем случае переменной pos присваивается значение параметра цикла i).
Найдите минимальное значение в некоторой последовательности

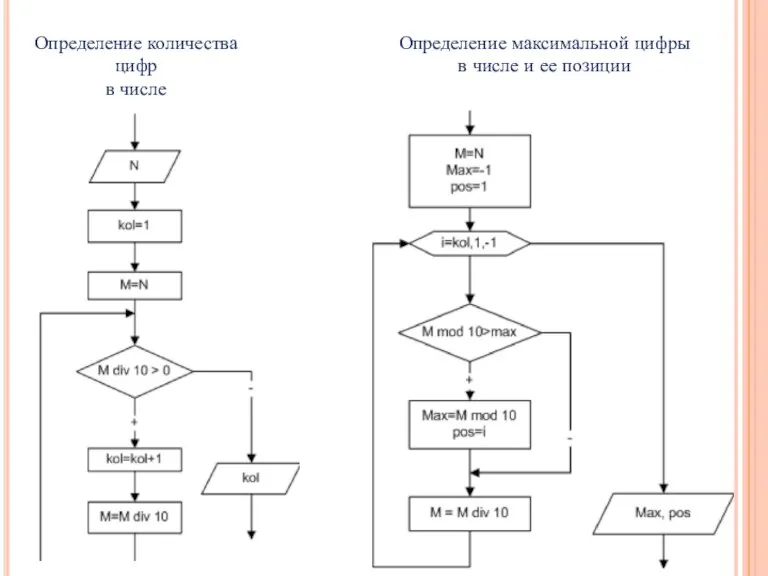
Определение максимальной цифры
в числе и ее позиции
Определение количества цифр
в числе