Содержание
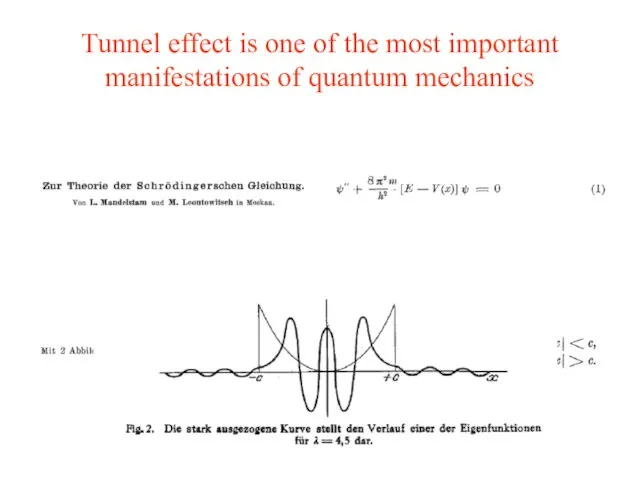
- 2. Tunnel effect is one of the most important manifestations of quantum mechanics
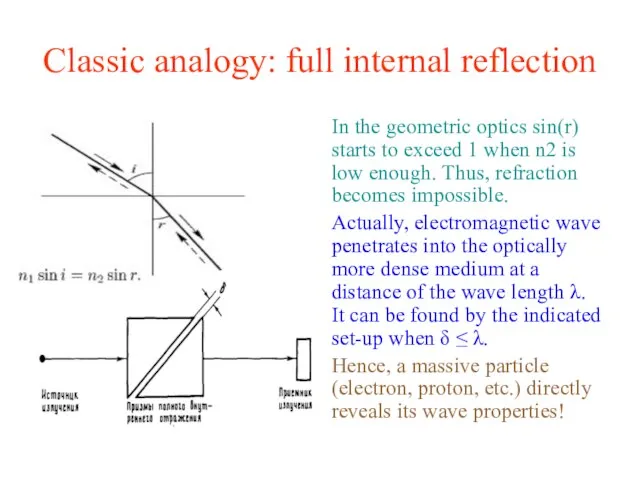
- 3. Classic analogy: full internal reflection In the geometric optics sin(r) starts to exceed 1 when n2
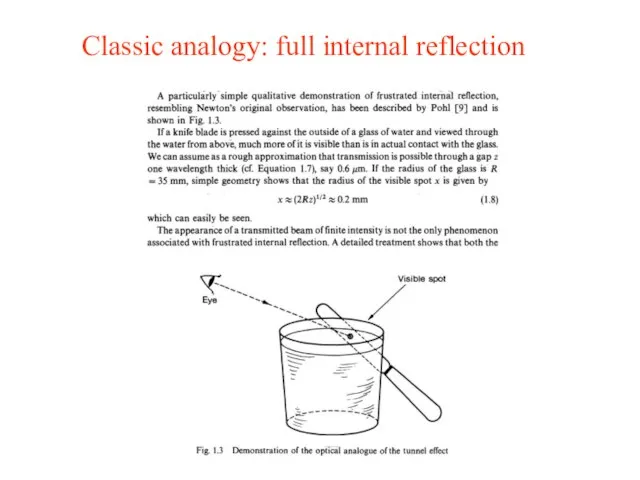
- 4. Classic analogy: full internal reflection
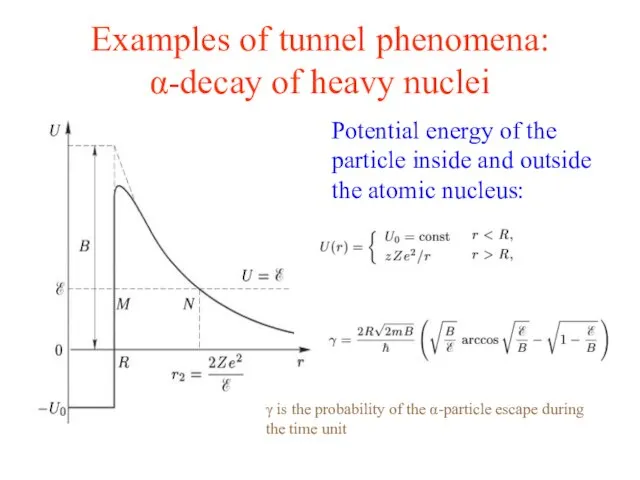
- 5. Examples of tunnel phenomena: α-decay of heavy nuclei Potential energy of the particle inside and outside
- 6. Scientists, who discovered the tunnel effect
- 7. Scientists, who discovered the tunnel effect
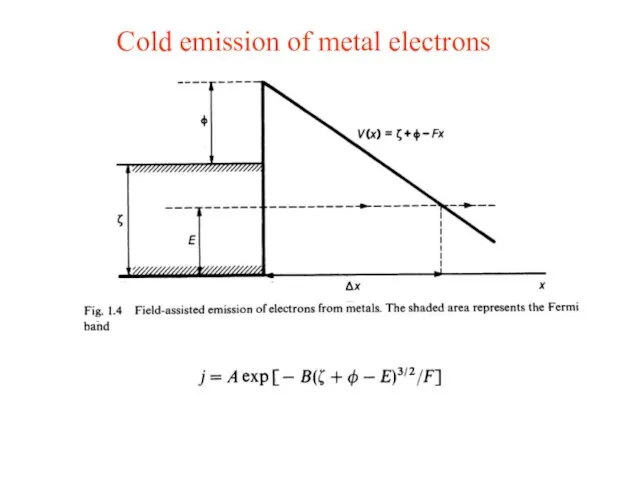
- 8. Cold emission of metal electrons Cold emission current E is the external electrostatic field
- 9. Cold emission of metal electrons
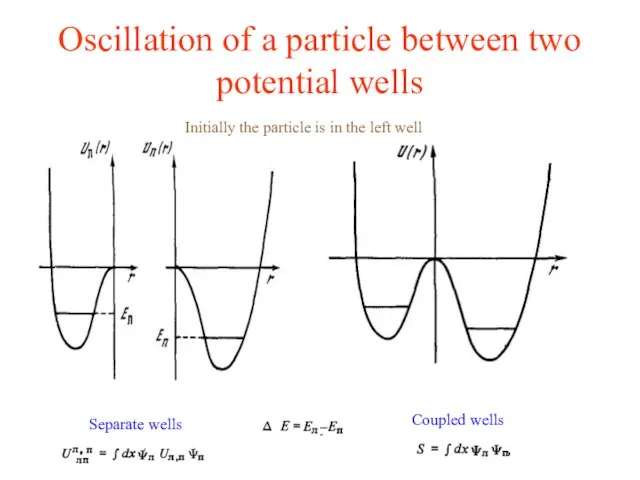
- 10. Oscillation of a particle between two potential wells Separate wells Coupled wells Initially the particle is
- 11. Oscillation of a particle between two potential wells Results of calculation: W(t) is a probability of
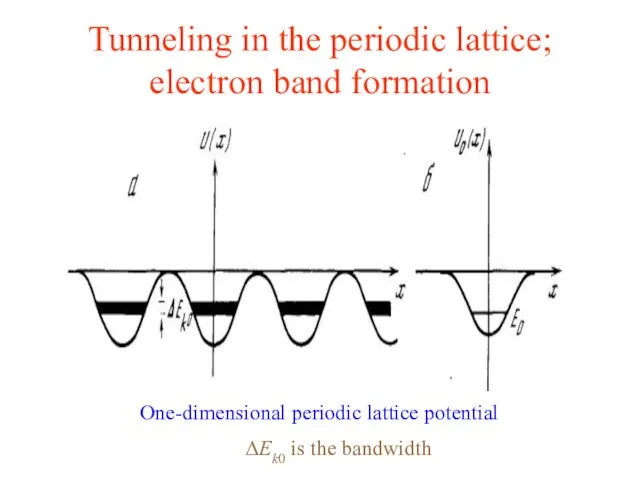
- 12. Tunneling in the periodic lattice; electron band formation One-dimensional periodic lattice potential ΔEk0 is the bandwidth
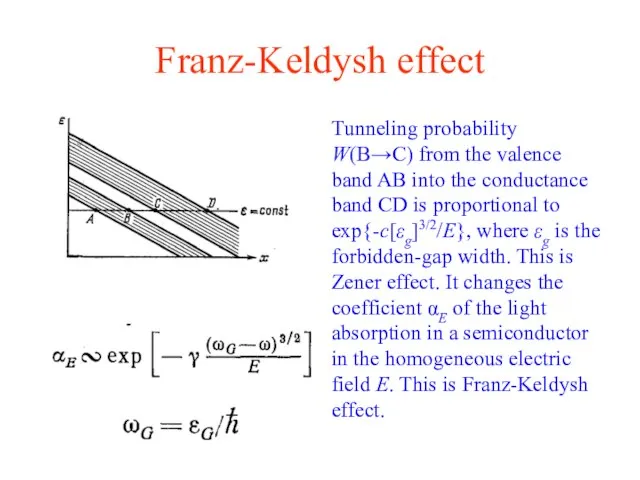
- 13. Franz-Keldysh effect Tunneling probability W(B→C) from the valence band AB into the conductance band CD is
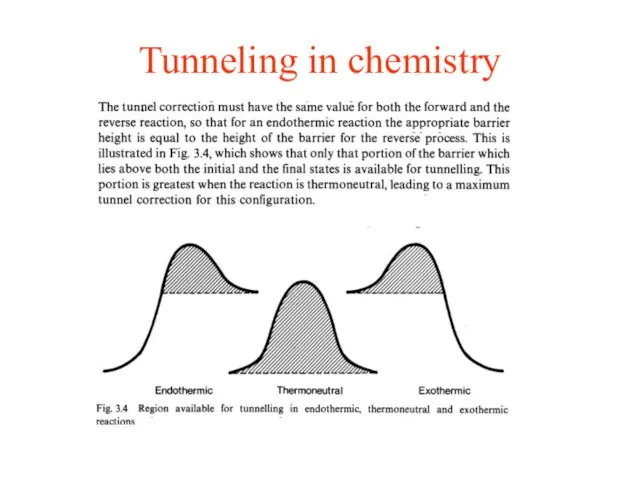
- 14. Tunneling in chemistry
- 15. Tunneling in chemistry
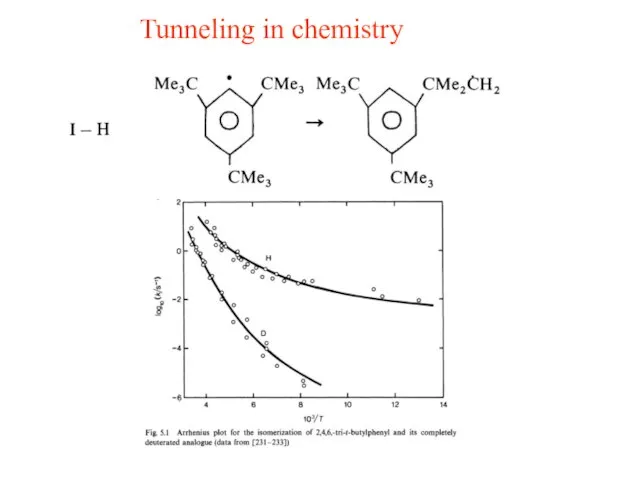
- 16. Tunneling in chemistry
- 17. Tunneling in chemistry
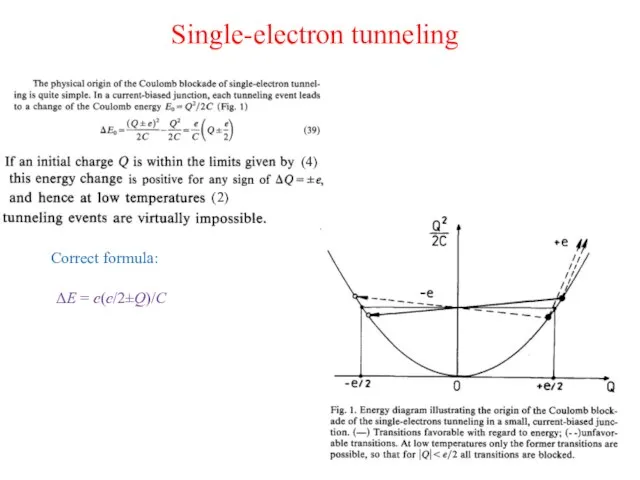
- 18. Single-electron tunneling
- 19. Single-electron tunneling (4) (2) ΔE = e(e/2±Q)/C Correct formula:
- 20. Single-electron tunneling
- 22. Скачать презентацию








 Познай Беларусь
Познай Беларусь Казачья сказка
Казачья сказка МИРОВОЙ ОПЫТ ПРИМЕНЕНИЯ СОРБЕНТА АНФЕЖ® ДЛЯ РАДИОХИМИЧЕСКОГО АНАЛИЗА ПРИРОДНЫХ ВОД
МИРОВОЙ ОПЫТ ПРИМЕНЕНИЯ СОРБЕНТА АНФЕЖ® ДЛЯ РАДИОХИМИЧЕСКОГО АНАЛИЗА ПРИРОДНЫХ ВОД Эксплуатация автомобильного транспорта
Эксплуатация автомобильного транспорта Золотая хохлома
Золотая хохлома Зимние олимпийские игры
Зимние олимпийские игры Портфолио
Портфолио ЖЕНИТЕ са много добри В БИЗНЕСА. - презентация
ЖЕНИТЕ са много добри В БИЗНЕСА. - презентация Меншік туралы осымша апарат
Меншік туралы осымша апарат Любимый город на Шексне (предприятия города)
Любимый город на Шексне (предприятия города) Реформа армии и военного управления Петра I
Реформа армии и военного управления Петра I Портрет профессии
Портрет профессии От Лиги наций к ООН. Тема 3
От Лиги наций к ООН. Тема 3 «Психологический климат в семье как основа формирования личности ребенка»( родительское собрание)
«Психологический климат в семье как основа формирования личности ребенка»( родительское собрание) Правила для велосипедистов
Правила для велосипедистов История вышивки лентами
История вышивки лентами Алексей Архипович Леонов Художник – фантаст
Алексей Архипович Леонов Художник – фантаст Радио RECORD
Радио RECORD Доклад Роснауке, (Федеральное агентство по науке и инновациям) Москва, 30 мая 2006 г. "ГОИ имени С.И. ВАВИЛОВА - от прошлого к Будущему"
Доклад Роснауке, (Федеральное агентство по науке и инновациям) Москва, 30 мая 2006 г. "ГОИ имени С.И. ВАВИЛОВА - от прошлого к Будущему"  Изготовление бас-гитары
Изготовление бас-гитары Где логика? Игра
Где логика? Игра Окружающий мир 2 класс
Окружающий мир 2 класс Анималистический жанр в изобразительном искусстве (скульптура, графика)
Анималистический жанр в изобразительном искусстве (скульптура, графика) Презентация на тему Демьян Степанович Станюкович
Презентация на тему Демьян Степанович Станюкович ПРОЕКТ СТРОИТЕЛЬСТВА
ПРОЕКТ СТРОИТЕЛЬСТВА Фёдор Михайлович Достоевский 1821-1881
Фёдор Михайлович Достоевский 1821-1881 Россия в лирике А.Блока и картинах русских художников конца 19 - начала 20 вв
Россия в лирике А.Блока и картинах русских художников конца 19 - начала 20 вв Презентация на тему тихий дон шолохов
Презентация на тему тихий дон шолохов