Содержание
- 2. Немного теории Для решения данного вида задач необходимо знать, что такое концентрация вещества в смеси (растворе
- 3. Процентным содержанием компонента А называется число рА= сА 100%, т.е. это концентрация вещества, выраженная в процентах.
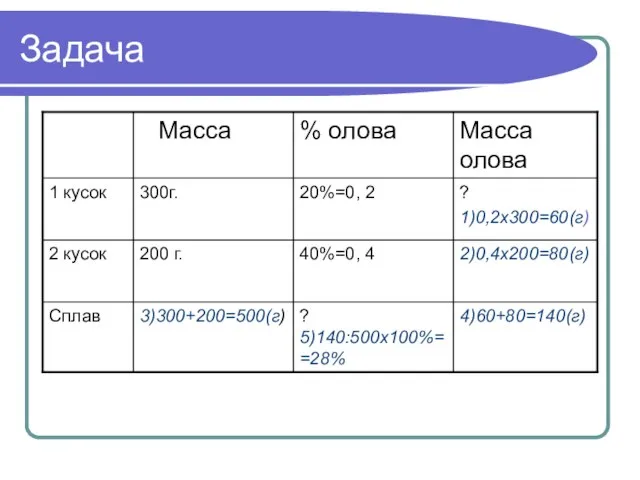
- 4. Задача
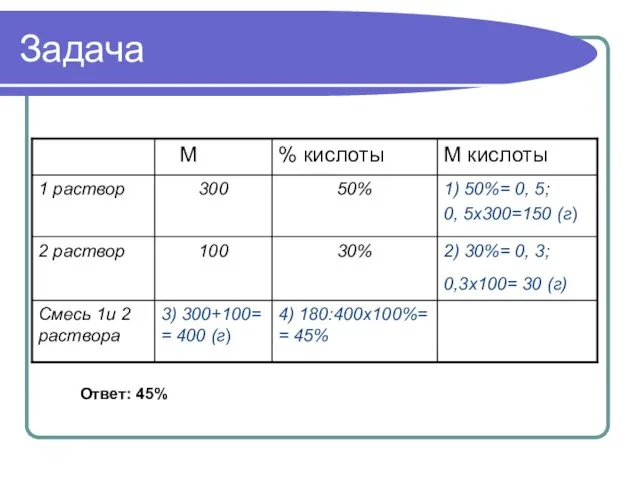
- 5. Задача Ответ: 45%
- 6. Алгоритм решения задач такого типа 1) 2) 3) 4) 5) Масса олова в первом куске. Масса
- 9. При решении задач данного типа полезно пользоваться наглядной моделью — схемой, в которой смесь (раствор, сплав)
- 10. Пример 1. Имеются два сплава меди со свинцом. Один сплав содержит15% меди, а другой 65%. Сколько
- 11. Сверху подпишем названия компонентов сплавов. Обычно бывает достаточно указать первые буквы в их названиях (если они
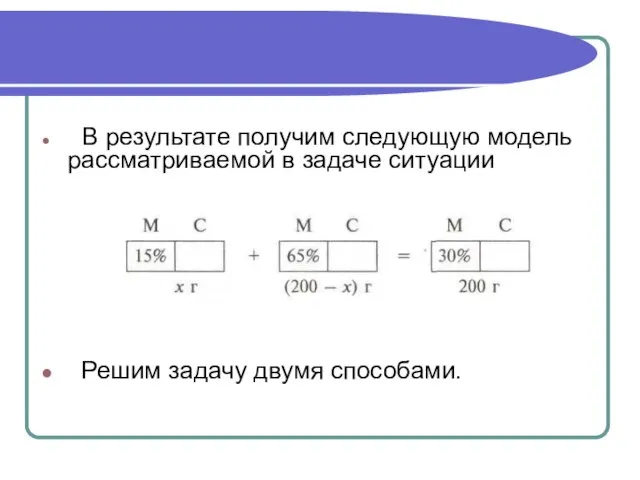
- 12. В результате получим следующую модель рассматриваемой в задаче ситуации Решим задачу двумя способами.
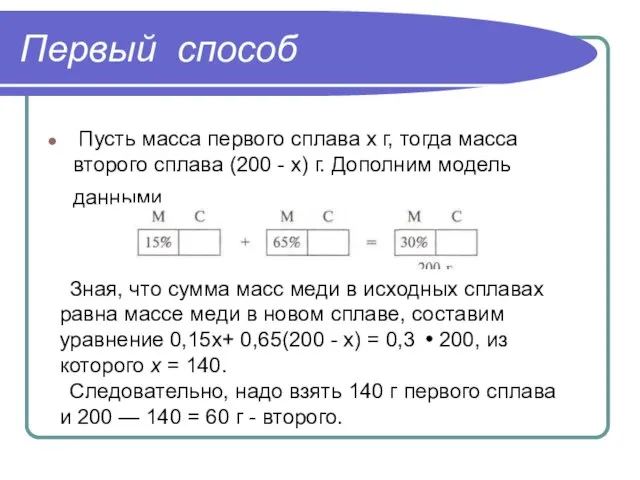
- 14. Первый способ Пусть масса первого сплава х г, тогда масса второго сплава (200 - х) г.
- 15. Второй способ. Можно обозначить х г и у г массу первого и второго сплава соответственно. Очевидно,
- 16. Замечание. Обратите внимание на то, что в любом из рассмотренных способов решения можно было составить уравнение
- 17. Пример 2. В 4 кг сплава меди и олова содержится 40% олова. Сколько килограммов олова надо
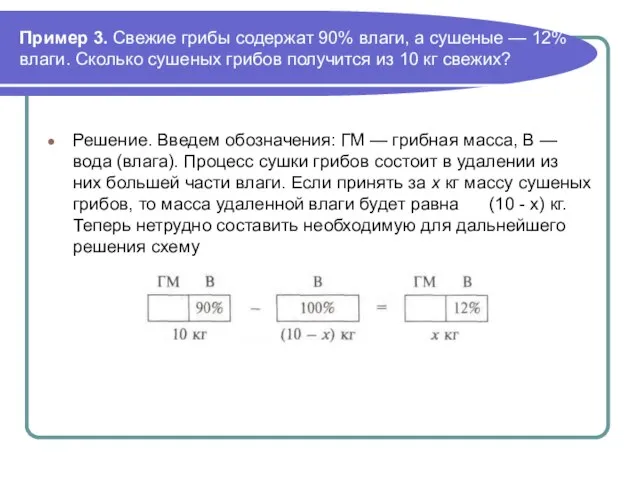
- 18. Пример 3. Свежие грибы содержат 90% влаги, а сушеные — 12% влаги. Сколько сушеных грибов получится
- 19. Можно составить уравнение на основе подсчета масс влаги, учитывая, что она удаляется из грибов: 0,9 10-(10-х)
- 20. Пример 4. Из 40 т железной руды выплавляют 20 т стали, содержащей 6% примесей. Каков процент
- 21. Задача. Из бака емкостью 54 л, наполненного кислотой, вылили несколько литров и долили водой. Потом опять
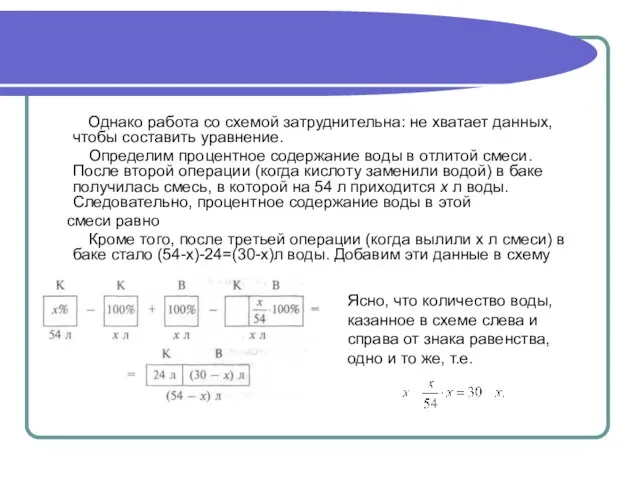
- 22. Однако работа со схемой затруднительна: не хватает данных, чтобы составить уравнение. Определим процентное содержание воды в
- 23. 54х-х² =1620-54х; х² -108х+1620=0. Корни уравнения: х=90, х=18. Первый корень не подходит по смыслу задачи (нельзя
- 25. Скачать презентацию














 Денежные переводы физических лиц: состояние и тенденции развития (на примере ПАО Сбербанк)
Денежные переводы физических лиц: состояние и тенденции развития (на примере ПАО Сбербанк) Особенности истории информатики
Особенности истории информатики Мотивирование топ-менеджеров в банковской сфере: подходы и инструменты
Мотивирование топ-менеджеров в банковской сфере: подходы и инструменты = 1
= 1 Изустная среда мордовского села
Изустная среда мордовского села Показатели рыночной активности
Показатели рыночной активности Выхухоль. Красная книга
Выхухоль. Красная книга Обработка текстовой и графической информации. Создаём комбинированный документ
Обработка текстовой и графической информации. Создаём комбинированный документ Телевидение: я выбираю или меня выбирают. Автор и руководитель проекта: Симонова Ольга Владимировна 2004 год
Телевидение: я выбираю или меня выбирают. Автор и руководитель проекта: Симонова Ольга Владимировна 2004 год Что я сделаю, чтобы доверенный мне магазин стал лучшим на рынке
Что я сделаю, чтобы доверенный мне магазин стал лучшим на рынке Туалетная вода для мужчин Faberlic Intense
Туалетная вода для мужчин Faberlic Intense Межпроцедурные анализы и оптимизации
Межпроцедурные анализы и оптимизации Внешняя политика СССР в 1930-е гг. и накануне Великой Отечественной войны
Внешняя политика СССР в 1930-е гг. и накануне Великой Отечественной войны Урок 3 Человек и Бог в православии-повторение
Урок 3 Человек и Бог в православии-повторение 17 век
17 век ПЕРЕГОВОРЫ
ПЕРЕГОВОРЫ Изготовление вечернего платья
Изготовление вечернего платья Теорiя iгор
Теорiя iгор  Презентация на тему Роль гормонов в обмене веществ, росте и развитии организма биология 8 класс
Презентация на тему Роль гормонов в обмене веществ, росте и развитии организма биология 8 класс аня хочет санчо панчо
аня хочет санчо панчо Создание таблиц в Microsoft Word
Создание таблиц в Microsoft Word Teenagers’ society problems
Teenagers’ society problems Воля познавать
Воля познавать Любимое блюдо моей семьи
Любимое блюдо моей семьи Ладья. Урок №8
Ладья. Урок №8 Описательные характеристики распределения тестовых результатов
Описательные характеристики распределения тестовых результатов Презентация на тему Одиночество
Презентация на тему Одиночество Ich gehe mit meine Laterne
Ich gehe mit meine Laterne