Содержание
- 2. ПЛАНИРОВАНИЕ ПРОЕКТА
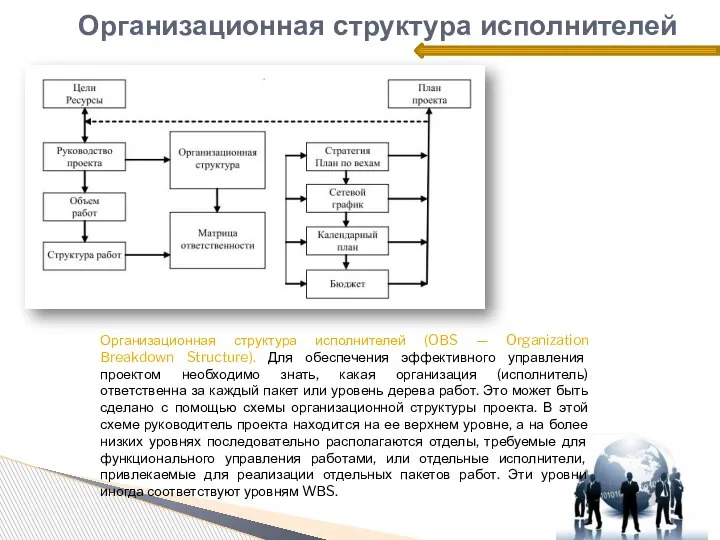
- 3. Организационная структура исполнителей Организационная структура исполнителей (OBS — Organization Breakdown Structure). Для обеспечения эффективного управления проектом
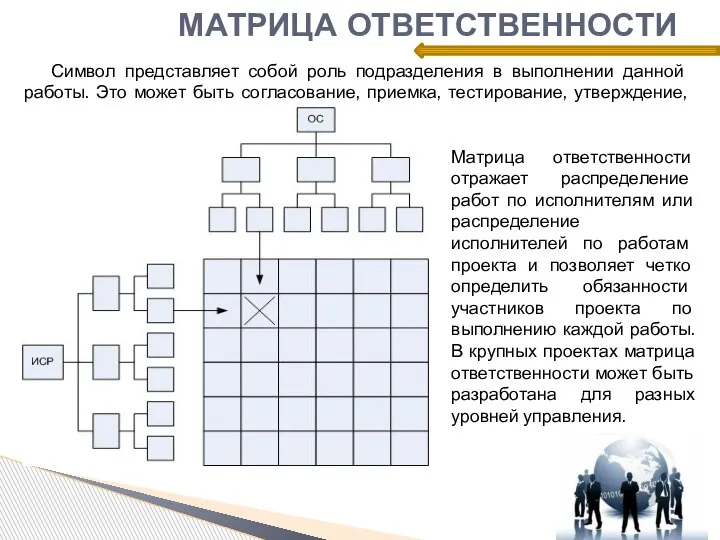
- 4. МАТРИЦА ОТВЕТСТВЕННОСТИ Символ представляет собой роль подразделения в выполнении данной работы. Это может быть согласование, приемка,
- 5. Матрица ответственности
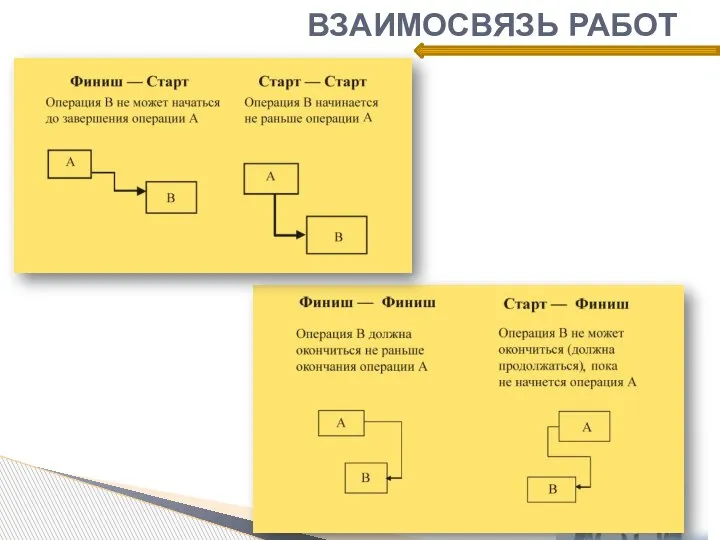
- 6. ВЗАИМОСВЯЗЬ РАБОТ
- 7. ОЦЕНКА ПРОДОЛЖИТЕЛЬНОСТИ РАБОТ Для оценки продолжительностей работ может использоваться следующая исходная информация: перечень работ проекта нижнего
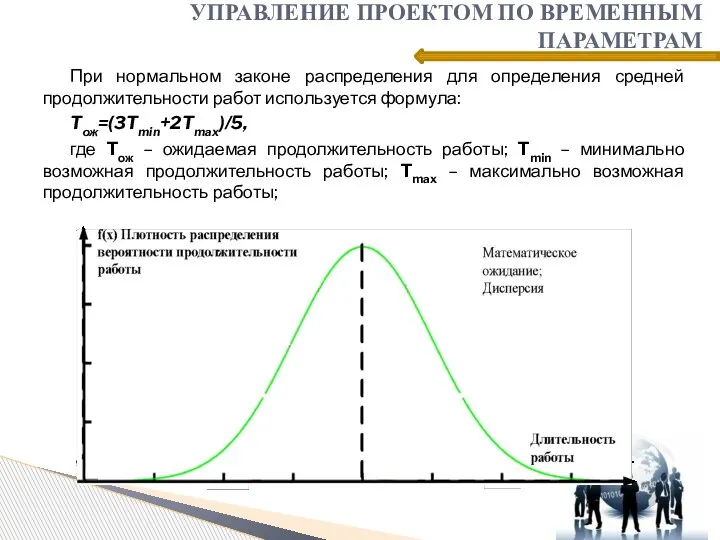
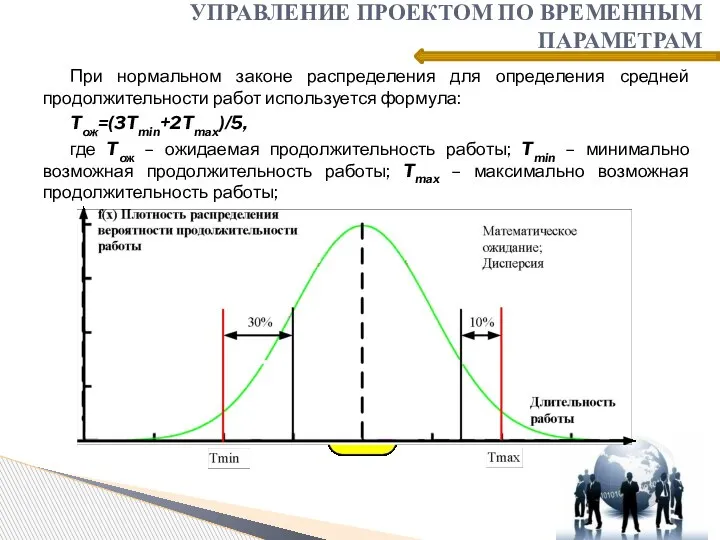
- 8. При нормальном законе распределения для определения средней продолжительности работ используется формула: Tож=(3Tmin+2Tmax)/5, где Tож – ожидаемая
- 9. При нормальном законе распределения для определения средней продолжительности работ используется формула: Tож=(3Tmin+2Tmax)/5, где Tож – ожидаемая
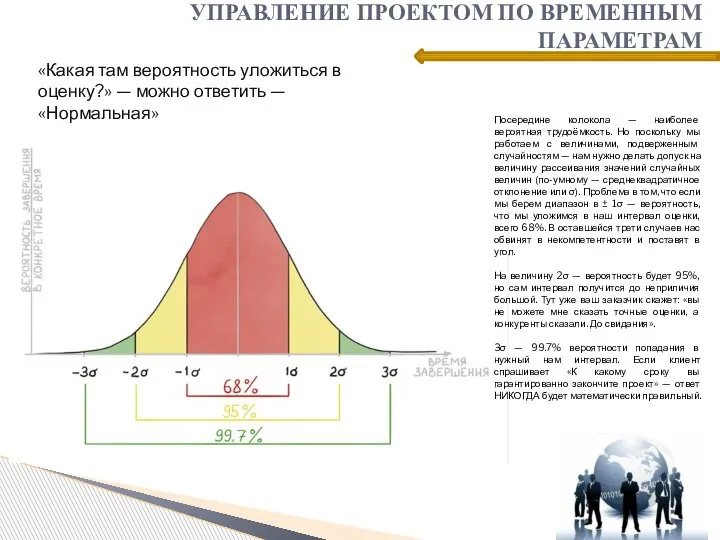
- 10. УПРАВЛЕНИЕ ПРОЕКТОМ ПО ВРЕМЕННЫМ ПАРАМЕТРАМ «Какая там вероятность уложиться в оценку?» — можно ответить — «Нормальная»
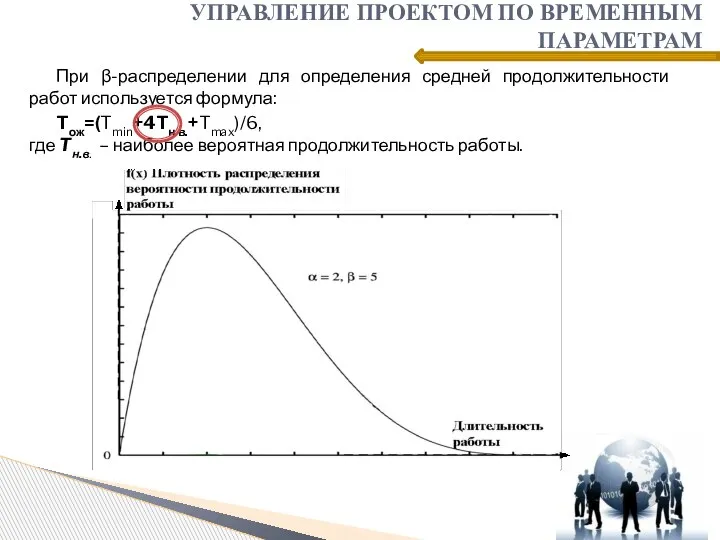
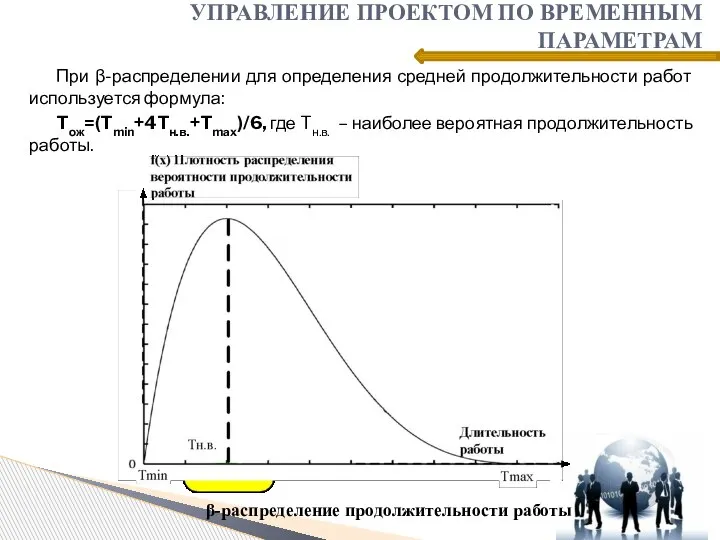
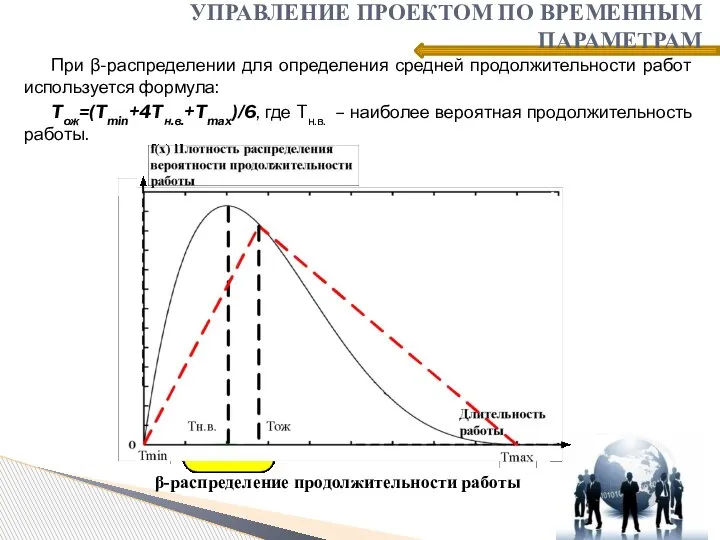
- 11. При β-распределении для определения средней продолжительности работ используется формула: Tож=(Tmin+4Tн.в.+Tmax)/6, где Tн.в. – наиболее вероятная продолжительность
- 12. При β-распределении для определения средней продолжительности работ используется формула: Tож=(Tmin+4Tн.в.+Tmax)/6, где Tн.в. – наиболее вероятная продолжительность
- 13. При β-распределении для определения средней продолжительности работ используется формула: Tож=(Tmin+4Tн.в.+Tmax)/6, где Tн.в. – наиболее вероятная продолжительность
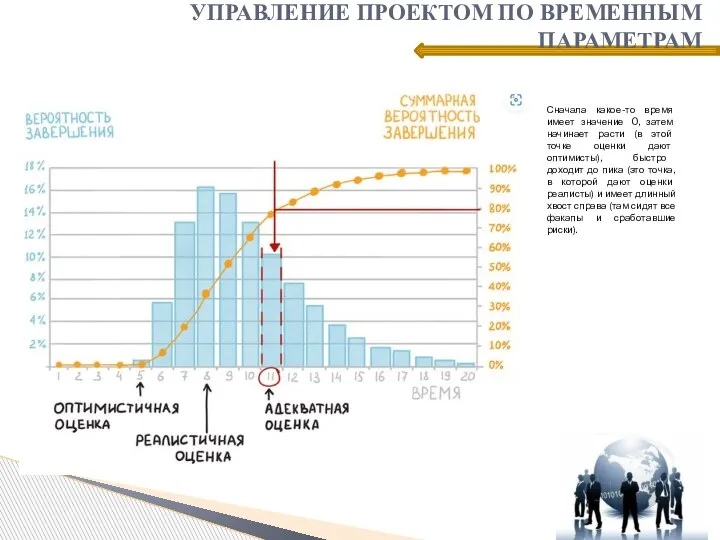
- 14. УПРАВЛЕНИЕ ПРОЕКТОМ ПО ВРЕМЕННЫМ ПАРАМЕТРАМ Сначала какое-то время имеет значение 0, затем начинает расти (в этой
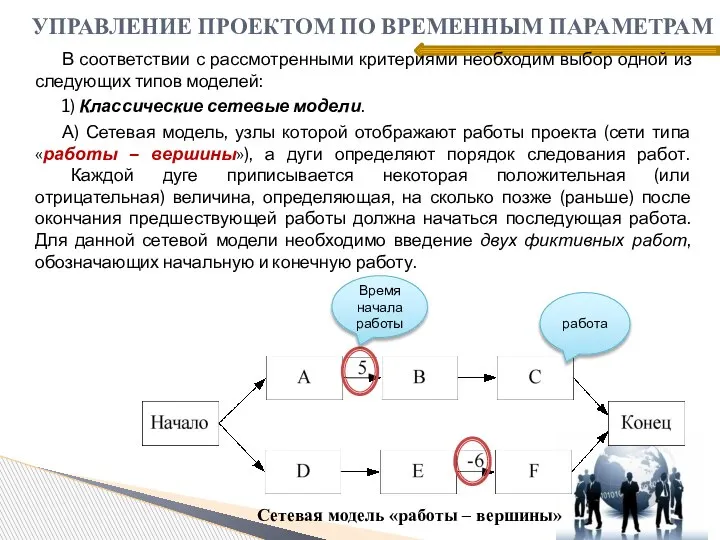
- 15. В соответствии с рассмотренными критериями необходим выбор одной из следующих типов моделей: 1) Классические сетевые модели.
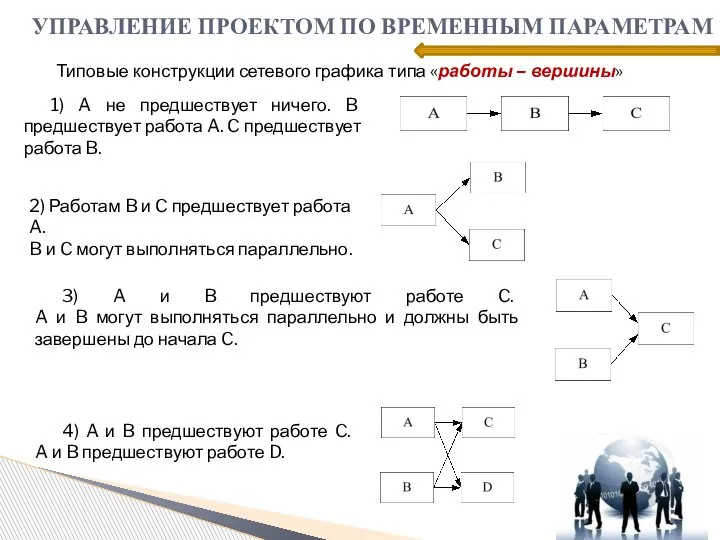
- 16. Типовые конструкции сетевого графика типа «работы – вершины» 2) Работам B и C предшествует работа A.
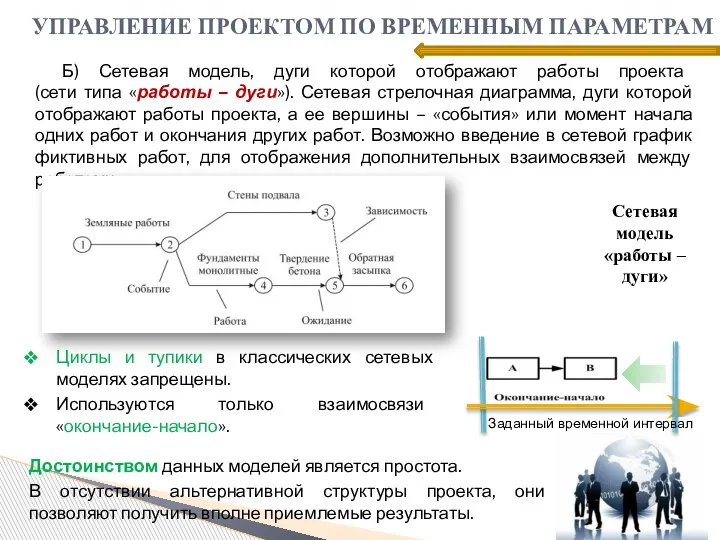
- 17. Б) Сетевая модель, дуги которой отображают работы проекта (сети типа «работы – дуги»). Сетевая стрелочная диаграмма,
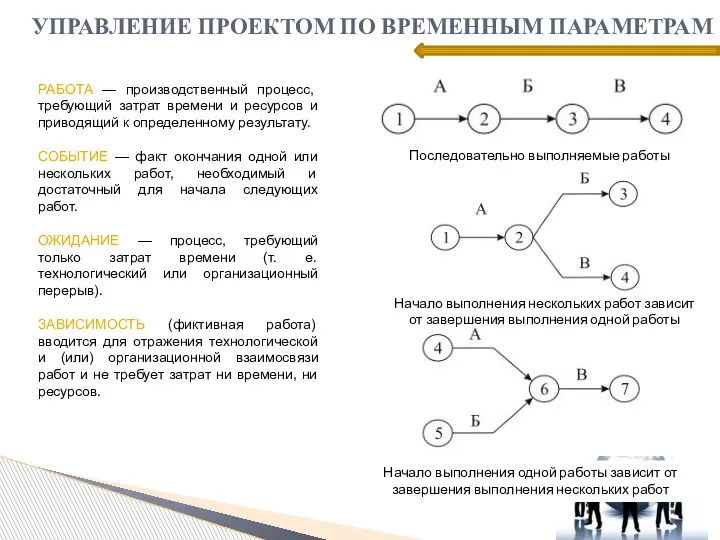
- 18. УПРАВЛЕНИЕ ПРОЕКТОМ ПО ВРЕМЕННЫМ ПАРАМЕТРАМ РАБОТА — производственный процесс, требующий затрат времени и ресурсов и приводящий
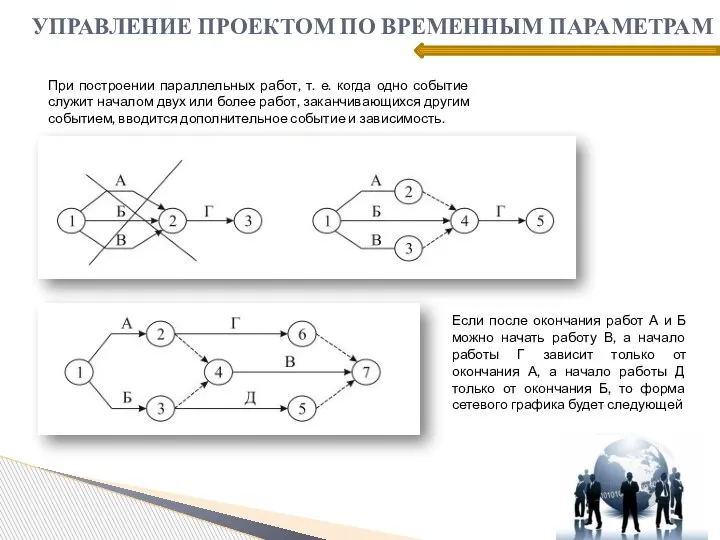
- 19. УПРАВЛЕНИЕ ПРОЕКТОМ ПО ВРЕМЕННЫМ ПАРАМЕТРАМ При построении параллельных работ, т. е. когда одно событие служит началом
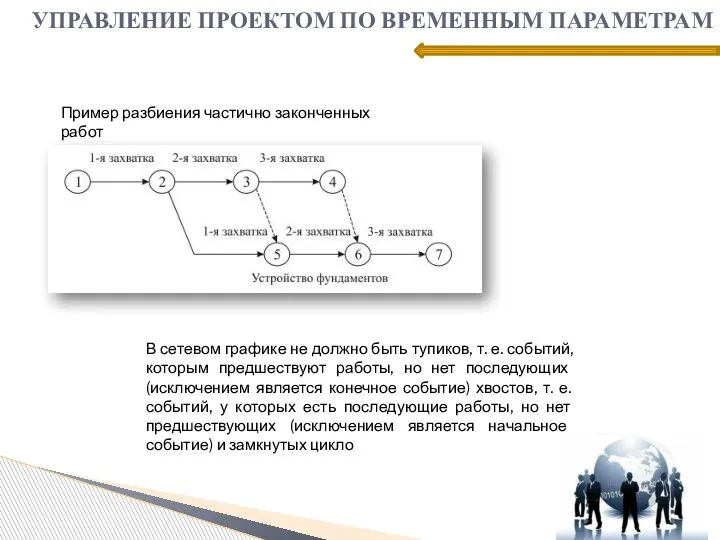
- 20. УПРАВЛЕНИЕ ПРОЕКТОМ ПО ВРЕМЕННЫМ ПАРАМЕТРАМ Пример разбиения частично законченных работ В сетевом графике не должно быть
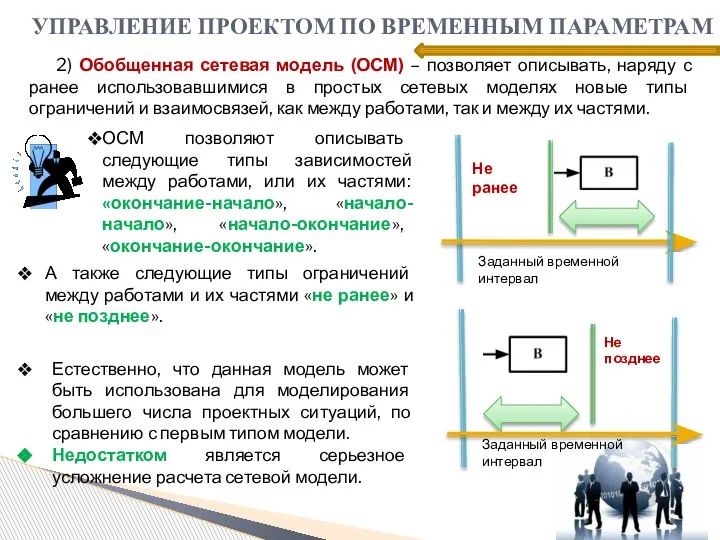
- 21. 2) Обобщенная сетевая модель (ОСМ) – позволяет описывать, наряду с ранее использовавшимися в простых сетевых моделях
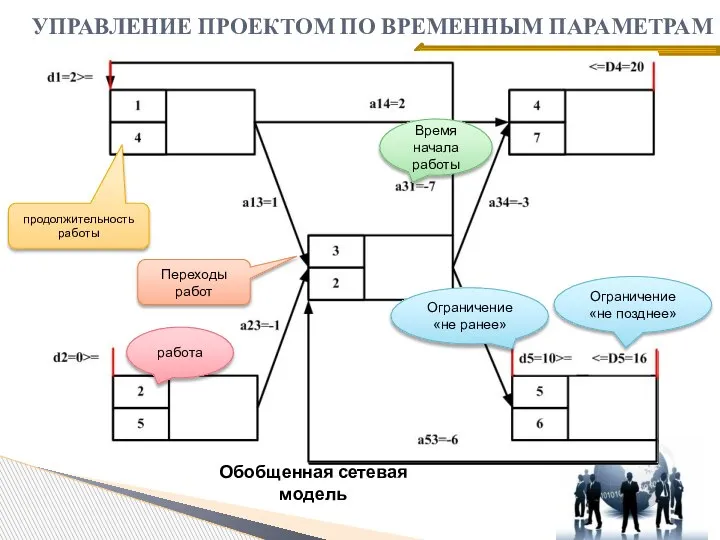
- 22. Обобщенная сетевая модель УПРАВЛЕНИЕ ПРОЕКТОМ ПО ВРЕМЕННЫМ ПАРАМЕТРАМ Время начала работы работа Ограничение «не ранее» Ограничение
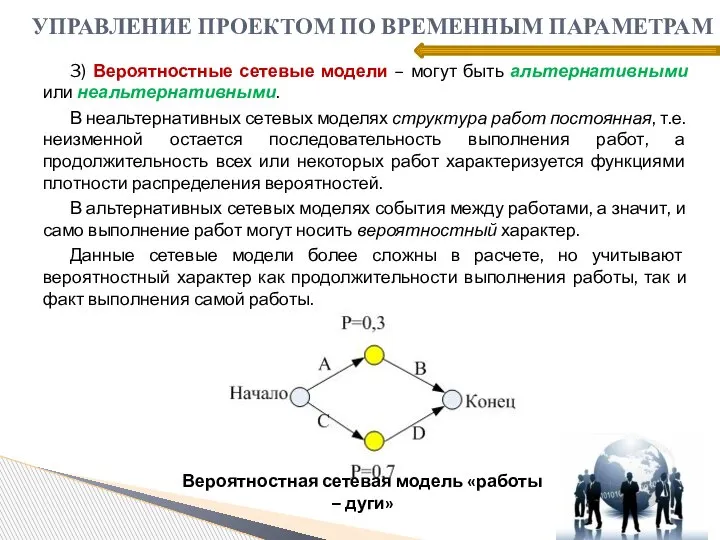
- 23. 3) Вероятностные сетевые модели – могут быть альтернативными или неальтернативными. В неальтернативных сетевых моделях структура работ
- 24. 3) Стохастические сетевые модели (GERT, VERT, CAAN, GAAN) – применяются когда затруднительно или невозможно однозначно определить,
- 26. Скачать презентацию




 Презентация на тему Учимся писать сочинение (элективный курс)
Презентация на тему Учимся писать сочинение (элективный курс) Психосинтез Ассаджиоли
Психосинтез Ассаджиоли Prezentatsia
Prezentatsia В.В. Жириновский как харизматический лидер
В.В. Жириновский как харизматический лидер Механика игры Спорт, как искусство
Механика игры Спорт, как искусство 27 мая - общероссийский День библиотек
27 мая - общероссийский День библиотек Принцип радиосвязи. Радиолокация
Принцип радиосвязи. Радиолокация Вклад женщин в развитие математики.
Вклад женщин в развитие математики. Моя Родина - Россия
Моя Родина - Россия Основные положения по проектированию усиления МК
Основные положения по проектированию усиления МК Старая Тверь
Старая Тверь Малювання зентангл
Малювання зентангл ПРИЛАГАТЕЛЬНЫЕ В ЛАТИНСКОМ ЯЗЫКЕ
ПРИЛАГАТЕЛЬНЫЕ В ЛАТИНСКОМ ЯЗЫКЕ 7рота
7рота Акварель
Акварель Источник права и их классификация
Источник права и их классификация Title
Title  ЭЛЕКТРОННЫЕ ТАБЛИЦЫ (табличный процессор MS Excel)
ЭЛЕКТРОННЫЕ ТАБЛИЦЫ (табличный процессор MS Excel) Индекс развития человеческого потенциала
Индекс развития человеческого потенциала Сохранение и уменьшение потребления энергии населением и предприятиями Томской области. Использование солнечных батарей
Сохранение и уменьшение потребления энергии населением и предприятиями Томской области. Использование солнечных батарей VI Съезд Подольской ТПП
VI Съезд Подольской ТПП INTELEKTUALA EKA: PIEREDZE UN TEHNOLOGIJU INTEGRACIJA
INTELEKTUALA EKA: PIEREDZE UN TEHNOLOGIJU INTEGRACIJA Как написать реферат? 10 класс
Как написать реферат? 10 класс Литература и искусство первой половины ХІХ века
Литература и искусство первой половины ХІХ века Образ человека в искусстве арабского Востока
Образ человека в искусстве арабского Востока Глухие дети. Психолого-педагогическая классификация нарушений слуховой функции у детей
Глухие дети. Психолого-педагогическая классификация нарушений слуховой функции у детей Действия для сохранения имущества семьи
Действия для сохранения имущества семьи Презентация
Презентация