Уравнение прямой видаy = kx + l

Уравнение прямой вида
y = kx + l
Линейное уравнение вида ax + by = с, у которого коэффициент b не равен 0 можно решить относительно у:
by = -ax + с
y = (-a/b)x + c/b
k l
или y = kx + l

Коэффициенты k и l
Рассмотрим, как зависит положение прямой y = kx + l от коэффициентов k и l.
Пусть l = 0. Тогда уравнение имеет вид y = kx. Если x = 0, то и y = 0. Т.е.
Прямая y = kx обязательно проходит через начало координат. Значит для ее построения необходимо найти только одну точку, принадлежащую графику, отличную от (0,0).

График уравнения y = kx
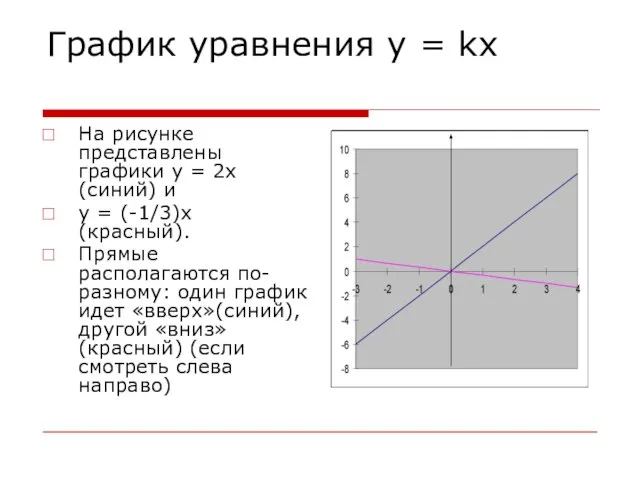
На рисунке представлены графики y = 2x (синий) и
у = (-1/3)х (красный).
Прямые располагаются по-разному: один график идет «вверх»(синий), другой «вниз»(красный) (если смотреть слева направо)

Коэффициент k
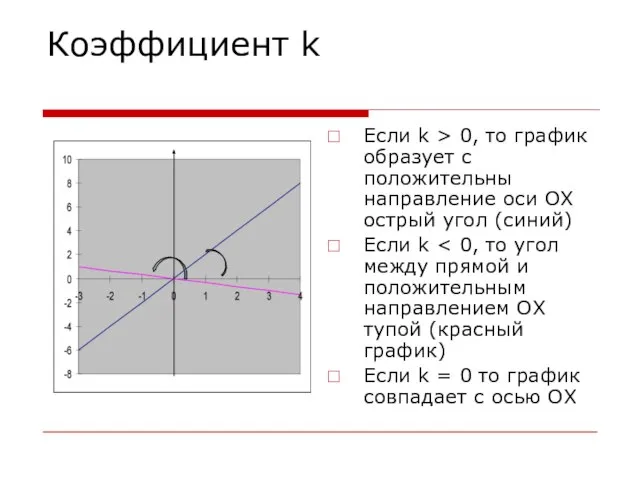
Если k > 0, то график образует с положительны направление оси ОХ острый угол (синий)
Если k < 0, то угол между прямой и положительным направлением ОХ тупой (красный график)
Если k = 0 то график совпадает с осью ОХ

k – угловой коэффициент
Если две прямые y = kx + l имеют одинаковый коэффициент k (угловой коэффициент) то графики этих прямых будут параллельны.
Если k различны, то прямые будут пересекаться.

Рассмотрим примеры
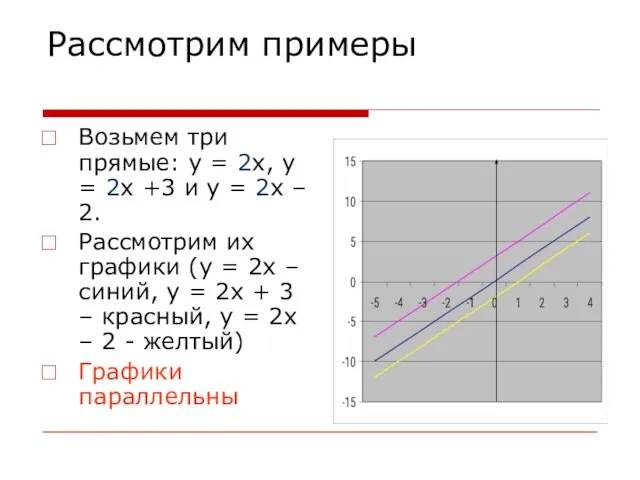
Возьмем три прямые: y = 2x, y = 2x +3 и у = 2х – 2.
Рассмотрим их графики (у = 2х – синий, у = 2х + 3 – красный, у = 2х – 2 - желтый)
Графики параллельны

Рассмотрим примеры
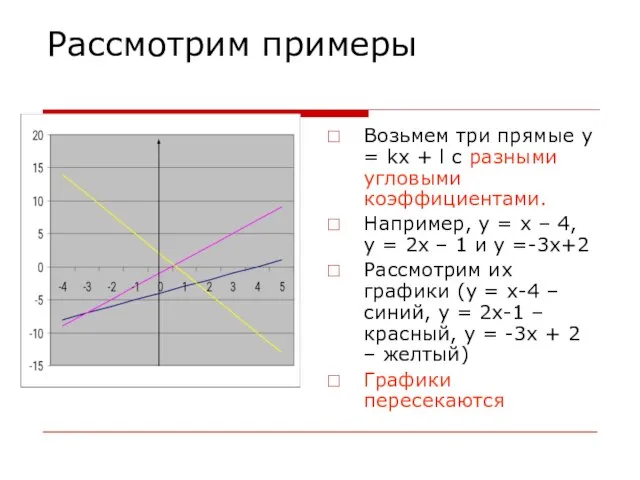
Возьмем три прямые у = kx + l с разными угловыми коэффициентами.
Например, y = x – 4, y = 2x – 1 и у =-3х+2
Рассмотрим их графики (у = х-4 – синий, у = 2х-1 – красный, у = -3х + 2 – желтый)
Графики пересекаются

Коэффициент l
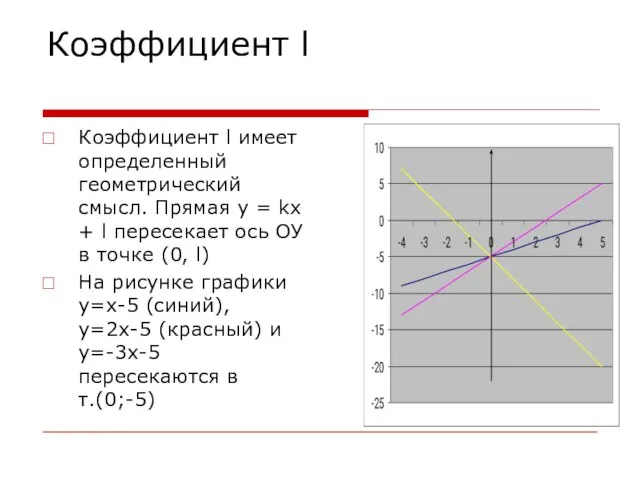
Коэффициент l имеет определенный геометрический смысл. Прямая y = kx + l пересекает ось ОУ в точке (0, l)
На рисунке графики y=x-5 (синий), у=2х-5 (красный) и у=-3х-5 пересекаются в т.(0;-5)