УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ (II)

Одним из наиболее распространенных уравнений с частными производными второго порядка является волновое уравнение, описывающее различные виды колебаний.

Одномерное волновое уравнение описывает продольные колебания стержня, сечения которого совершают плоскопараллельные колебательные движения.

Двумерное волновое уравнение используется для исследования колебаний тонкой пластины (мембраны).

Трехмерное волновое уравнение описывает распространение волн в пространстве (например, звуковых волн в жидко- жидкости).

Рассмотрим одномерное волновое уравнение
c начальными условиями

Рассмотрим явную разностную схему «крест» для решения данной задачи.

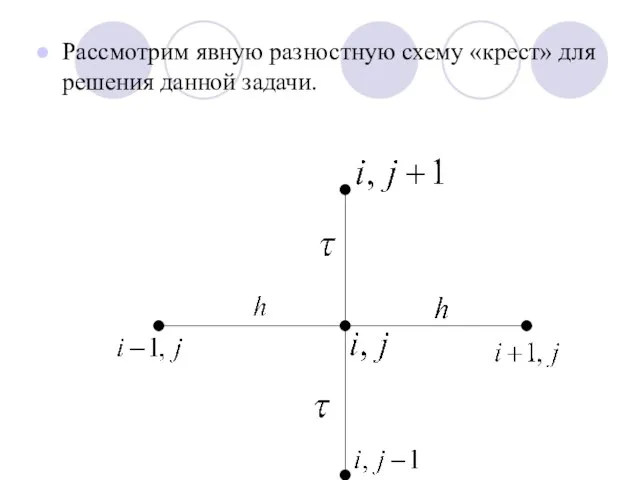
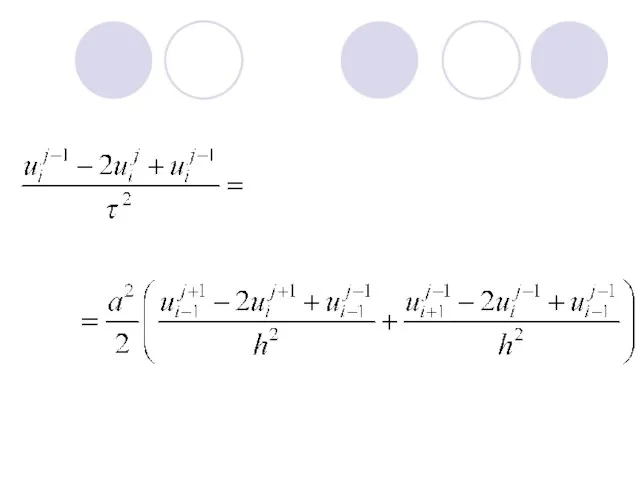
Заменим в уравнении вторые производные искомой функции U по t и х их конечно-разностными соотношениями.

Отсюда можно найти явное выражение для значения сеточной функции на (j + 1)-м слое:

Здесь, для определения неизвестных значений на (j + 1)-м слое нужно знать решения на j-м и (j — 1)-м слоях.
Поэтому начать счет можно лишь для второго слоя.

решения на нулевом и первом слоях находятся с помощью начальных условий.
На нулевом слое имеем

Для получения решения на первом слое воспользуемся вторым начальным условием.
Производную заменим конечно-разностной аппроксимацией.
Из этого соотношения можно найти значения сеточной функции на первом слое:

Построим неявную схему.
Вторую производную по t в уравнении аппроксимируем, как и ранее, по трехточечному шаблону с помощью значений сеточной функции на слоях j - 1, j, j + 1.

Из этого соотношения можно получить систему уравнений относительно неизвестных значений сеточной функции на (j + 1)-м слое:

ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Интегральным уравнением называется уравнение, неизвестная функция в котором содержится под знаком интеграла.
В общем случае интегральное уравнение имеет вид

Виды интегральных уравнений.
Уравнения, в которые искомая функция входит линейно, называются линейными интегральными уравнениями.

Одним из них является уравнение Фредгольма первого рода
Уравнение Фредгольма второго рода имеет вид

уравнение Вольтерра первого рода:
уравнение Вольтерра второго рода