Урок-консультация по теме « Решение показательных уравнений».

Организационный момент.
Устный счет.
Актуализация знаний .
Изучение нового материала.
Закрепление изученного материала.
Проверка и обсуждение заданий.
Итог урока.
Домашнее задание.
Ход урока

Устный счет.
1.Среди заданных функций укажите те, которые являются показательными:
Ответ: А); Г).
2.Какие из заданных функций являются возрастающими и какие, убывающими?
Ответ: А); В); Г).

Устный счет.
3. Решите уравнения.
Ответ: А) 3; Б)3 ;В)2 ;Г)4.
4. Решите уравнения.
Ответ: А)2;
; Г) -2.
5. Решите неравенства:
Г) нет решений.

Актуализация знаний
Показательное уравнение-это уравнение, содержащее неизвестное в показателе степени.
Основные методы решения
показательных уравнений
При b>0 данное уравнение решается логарифмированием обеих частей по основанию a
При b
0 уравнение
не имеет решений.

Решите уравнения:
Данное уравнение решений не имеет, т.к. -4<0,
а показательная функция принимает только положительные значения.

0,2
Решение показательных уравнений методом уравнивания показателей
т.е. преобразование данного уравнения к виду
а затем к виду
f(x)=g(x)
Решите уравнение
Приведем все степени к одному основанию 0,2. Получим уравнение
;
0,2
х=2х-3; х=3;
Ответ: х=3.

Решение показательных уравнений методом вынесения общего множителя за скобки.
7
Решите уравнение
Ответ: х=1

Решение показательных уравнений способом подстановки. С помощью удачной замены переменных некоторые показательные уравнения удается свести к алгебраическому виду, чаще всего к квадратному уравнению.
Решите уравнение
Решение.
Пусть
t>0
Тогда
Ответ:

Изучение нового материала
Метод почленного деления.
Способ группировки.
Графический метод решения уравнений.
Решение показательных уравнений методом подбора.
Другие методы решения показательных уравнений

Метод почленного деления.
Данный метод заключается в том, чтобы разделить каждый член уравнения, содержащий степени с одинаковыми показателями, но разными основаниями, на одну из степеней. Этот метод применяется для решения однородных показательных уравнений.
Решите уравнение
3
Решение
Пусть
Тогда
Далее имеем:
Ответ:

Способ группировки.
Способ группировки заключается в том, чтобы собрать степени с разными основаниями в разных частях уравнения, а затем разделить обе части уравнения на одну из степеней.
Решить уравнение
3
Решение.
Сгруппируем слагаемые следующим образом:
4,5
2х=-1
х=-0,5;
Ответ: х=-0,5

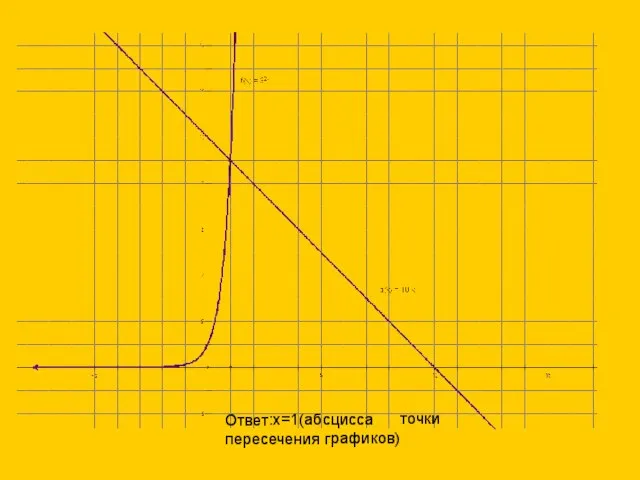
Использование графического метода решения уравнений.
Решить уравнение
Построим таблицы значений.

Ответ:х=1(абсцисса точки пересечения графиков)

Решение показательных уравнений методом подбора.
При решении показательных уравнений этим методом вначале находят путем подбора корень исходного уравнения, а затем доказывают, что этот корень единственный, с использованием свойства монотонности показательной функции.
Решить уравнение:
Решение:
Подбором находим, что х=2-корень исходного уравнения.
Покажем, что других корней нет.
Разделив исходное уравнение на
получаем равносильное уравнение:
А) Покажем, что среди чисел х<2 корней нет.
Если х<2, то
при х<2 корней нет.

Б) Покажем, что среди чисел х>2 корней исходного уравнения также нет.
Если х >2, то
при х>2 исходное уравнение корней не имеет.
Ответ: х=2.

Закрепление изученного материала.
Каждой группе учащихся в конвертах даются задания. Консультант раздает каждому ученику по одной задаче и через 10 минут решения собираются и сдаются учителю. Затем продолжается обсуждение и решение в группе остальных уравнений.

Задания группам.
Решить уравнения.
1.Решить графическим способом
2.Решить уравнение:
3.Решить уравнение :
4. Решить уравнение:

Проверка и обсуждение заданий.
Готовые решения одного из трех заданий записываются на доске каждой группой. Выдвинутый группой ученик объясняет решение, основываясь на теории, выдвигает алгоритм действий.