УСЛОВНО ИЗРАВНЕНИЕ НА ПЛАНОВИ/ДВУМЕРНИ МРЕЖИ. ОСНОВНИ ФИГУРИ

ОСНОВНИ ФИГУРИ
Триъгълник
Централна фигура
Геодезически четириъгълник
Венечна система

1. УСЛОВНО ИЗРАВНЕНИЕ НА ОТДЕЛЕН ТРИЪГЪЛНИК

a
b
c
β1
β2
β3

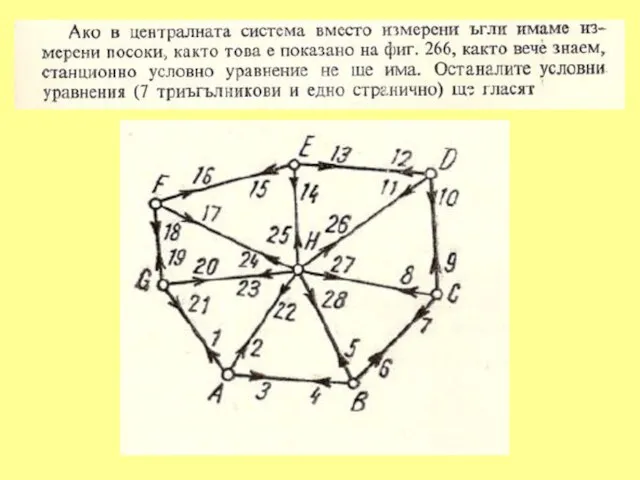
1. УСЛОВНО ИЗРАВНЕНИЕ НА ЦЕНТРАЛНА СИСТЕМА

Развитието на една функция в Тейлоров ред в общ вид е
F(X) = f{(x1+h1), {(x2+h2), . . ., {(xn+hn)} = f (x1, x2, . . . , xn) +
+ ∂f/∂x1.h1 + ∂f/∂x2.h2 + …+ ∂f/∂xn.hn + …

sin {(1) + v1}. sin {(3) + v3}. sin {(5) + v5}
F(X) = ─────────────────────────── - 1 = 0
sin {(2) + v2}. sin {(4) + v4}. sin {(6) + v6}
cos (1). sin (1). sin (3). sin (5) cos (2). sin (1). sin (3). sin (5)
F(X) = F (0) + ───────────────── v1- ────────────────── v2 +
sin (1). sin (2) . sin (4). sin (6) sin2 (2). sin (4). sin (6)
cos (3). sin (3). sin (1). sin (5) cos (4). sin (1). sin (3). sin (5)
+ ───────────────── v3 - ────────────────── v4 + . . . = 0
sin (3). sin (2) . sin (4). sin (6) sin2 (4). sin (4). sin (6)
Където
sin (1). sin (3). sin (5)
F (0) = ─────────────
sin (2) . sin (4). sin (6)

Означаваме : ctg (i) / ρcc = αi , където ρcc = 636620
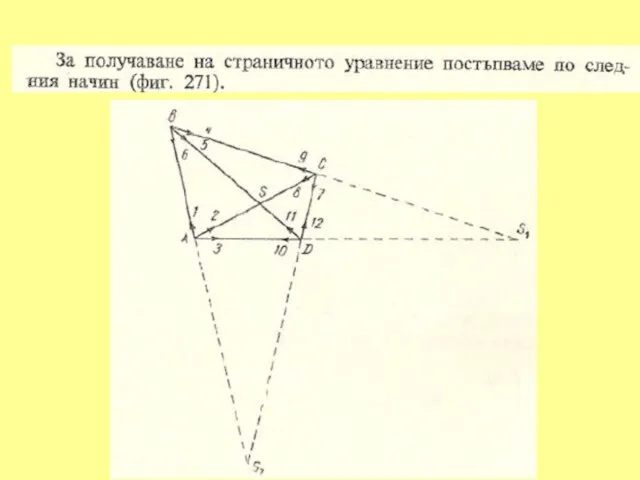
Тогава за страничното уравнение в окончателен линеен вид се получава
α1 v1 - α2v2 + α3v3 - α4v4 + α5v5 - α6v6 + w = 0
Така условните уравнения за по-голямата централна система ще бъдат

Общ вид на нормалните уравнения на корелатите :
[aa]K1 + [ab]K2 + [ac]K3 + . . . . . . . . . + [ar]Kr + w1 = 0
[ab]K1 + [bb]K2 + [bc]K3 + . . . . . . . . . + [br]Kr + w2 = 0
[ac]K1 + [bc]K2 + [cc]K3 + . . . . . . . . . + [cr]Kr + w3 = 0
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
[ar]K1 + [br]K2 + [cr]K3 + . . . . . . . . . . + [rr]Kr +wr = 0
vi = ai K1 + bi K2 + ci K3+ . . . . . + ri Kr
me = ± √[vv] / r

[aa/p]K1 + [ab/p]K2 + [ac/p]K3 + . . . . . . . . . + [ar/p]Kr + w1 = 0
[ab/p]K1 + [bb/p]K2 + [bb/p]K3 + . . . . . . . . . + [br/p]Kr + w2 = 0
[ac/p]K1 + [bc/p]K2 + [cc/p]K3 + . . . . . . . . . + [cr/p]Kr + w3 = 0
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
[ar/p]K1 + [br/p]K2 + [cr/p]K3 + . . . . . . . . . . + [rr/p]Kr + wr = 0
vi = ai/pi K1 + bi/pi K2 + ci/pi K3+ . . . . . + ri/pi Kr
me = ± √[pvv] / r

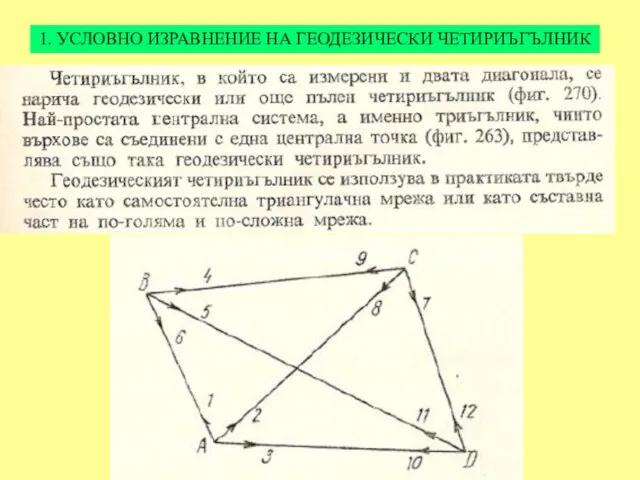
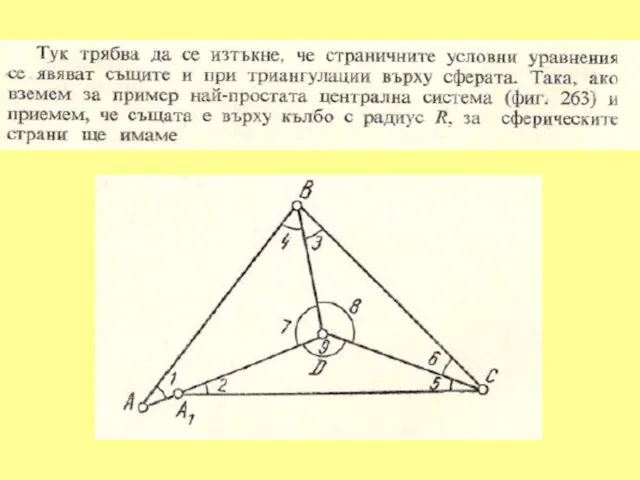
1. УСЛОВНО ИЗРАВНЕНИЕ НА ГЕОДЕЗИЧЕСКИ ЧЕТИРИЪГЪЛНИК

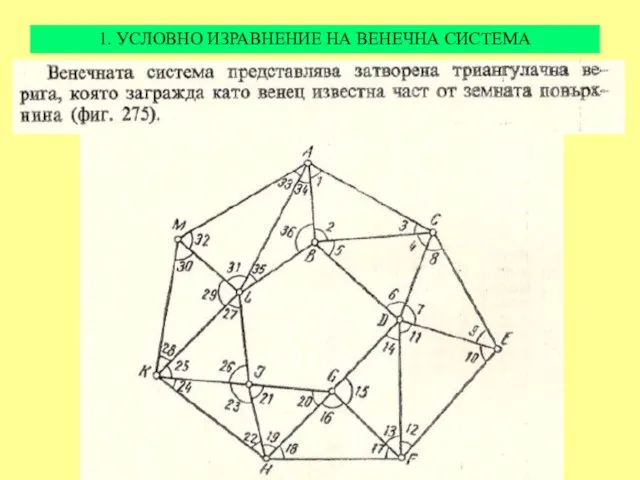
1. УСЛОВНО ИЗРАВНЕНИЕ НА ВЕНЕЧНА СИСТЕМА

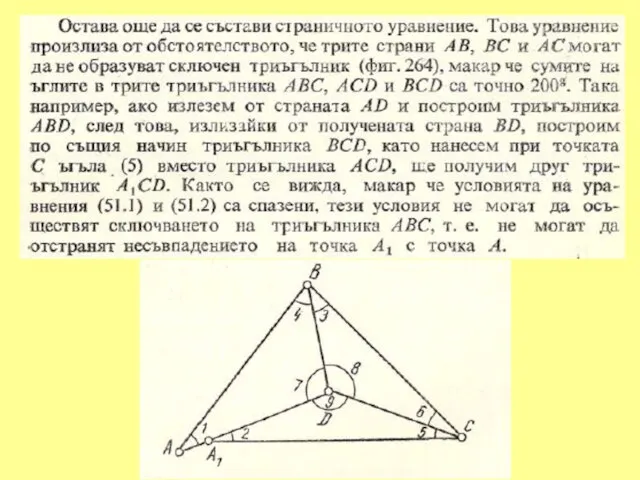
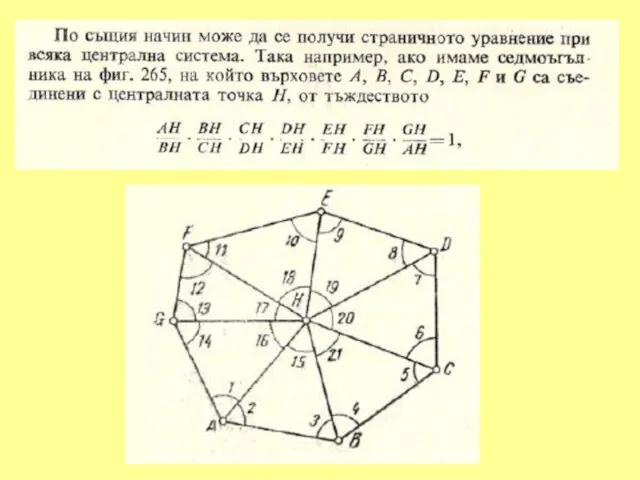
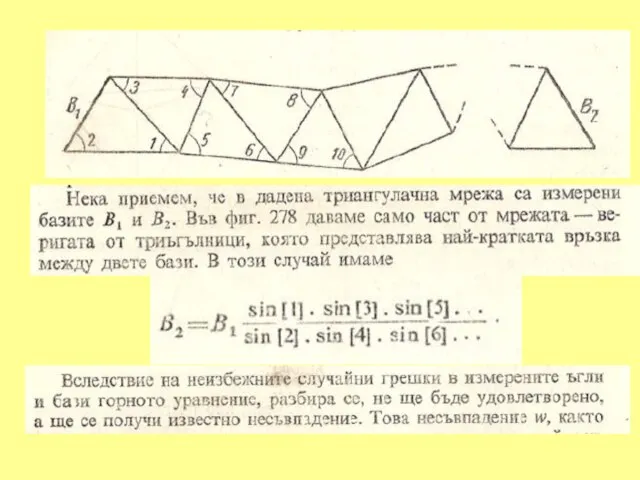
1. УСЛОВНО ИЗРАВНЕНИЕ СВОБОДНИ ЪГЛОВИ МРЕЖИ С ПОВЕЧЕ ОТ ЕДНА БАЗА