Содержание
- 2. Именно дроби помогают нам в жизни. Например, мама испекла пирог. После обеда осталось 5/8 пирога, во
- 3. Дробь – это частное от деления числителя на знаменатель. Так что же такое дробь? — ;
- 4. В жизни человеку приходилось не только считать предметы, но и измерять величины. Люди встретились с измерениями
- 5. Существуют обыкновенные, десятичные, правильные, неправильные дроби. И для них характерны различные правила: сложения, вычитания, умножения и
- 6. Народы прошли через многие варианты записи дробей, пока не пришли к современной записи. Вначале в записи
- 7. Древние ученые не считали числом результат деления дробных чисел. Например, 12/5=22/5 – дробный результат деления, но
- 8. Чтоб сложить дробь с дробью десятичной, Помни правило нетрудное отлично. Запиши одну дробь под другой. Запятая
- 9. Таким же образом мы действуем и при вычитании. Чтоб деление дробей было реальное, Преврати делитель в
- 10. Вначале уравнения, у которых в ответе получалось дробное число, считалось не имеющим решения, но постепенно в
- 11. Переход в расчетах на десятичные дроби очень помог практике. Кроме торговли, производства, картографии пользу испытала и
- 12. Изобретение десятичных дробей существенно продвинуло науку в создании счетных машин. Особенно хочется подчеркнуть, как важны точные
- 14. Скачать презентацию











 Ещё одна экскурсия в мой виртуальный музей
Ещё одна экскурсия в мой виртуальный музей Рисуем карандашом
Рисуем карандашом Барокко классицизм
Барокко классицизм Подростковый клуб Скаут. Проект
Подростковый клуб Скаут. Проект Разметка заготовок из древесины
Разметка заготовок из древесины Empire State Building
Empire State Building Презентация на тему Английские колонии в Северной Америке 7 класс
Презентация на тему Английские колонии в Северной Америке 7 класс 1 октября - День добра и уважения
1 октября - День добра и уважения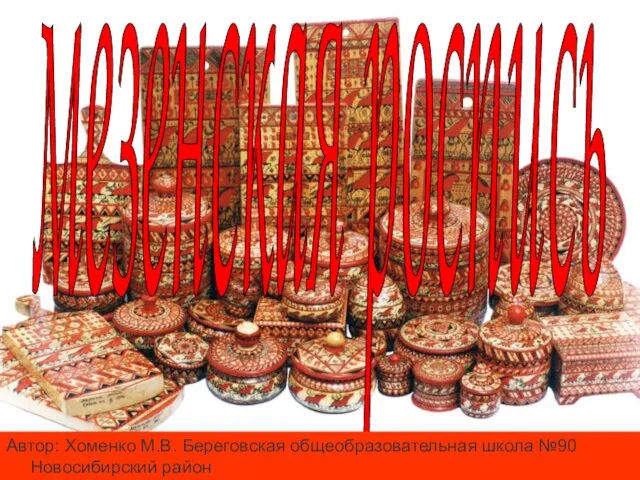 мезенская роспись
мезенская роспись Права ребенка
Права ребенка Кто под маской? Викторина
Кто под маской? Викторина Департамент образования Вологодской области
Департамент образования Вологодской области НОВЫЙ УЧЕБНЫЙ КУРС
НОВЫЙ УЧЕБНЫЙ КУРС Лесная промышленность
Лесная промышленность Презентация на тему Внешнее строение птиц. Строение перьев
Презентация на тему Внешнее строение птиц. Строение перьев Образ ворона в русской и зарубежной литературе
Образ ворона в русской и зарубежной литературе Система здравоохранения в Израиле
Система здравоохранения в Израиле Стиль Шебби-шик
Стиль Шебби-шик Экскурсия в лексический сад
Экскурсия в лексический сад Тургенев-сказочник
Тургенев-сказочник Тема: «Составление и использование игровых компьютерных презентаций на уроке товароведения пищевых продуктов»
Тема: «Составление и использование игровых компьютерных презентаций на уроке товароведения пищевых продуктов» Презентация на тему Развитие государства и права США в ХХ веке
Презентация на тему Развитие государства и права США в ХХ веке  Таможенная процедура – «Экспорта» Подготовили: Миронова Шайдуллина
Таможенная процедура – «Экспорта» Подготовили: Миронова Шайдуллина ПОЧАТОК Украинской революции
ПОЧАТОК Украинской революции  Самые страшные тюрьмы России и мира
Самые страшные тюрьмы России и мира Белоруссия 1941-1944гг
Белоруссия 1941-1944гг Обмен веществ и энергии в клетке
Обмен веществ и энергии в клетке Программа В.Ф.Виноградовой Начальная школа XXI века
Программа В.Ф.Виноградовой Начальная школа XXI века