Содержание
- 2. Примеры: поле температур, поле давления, поле плотности, поле концентраций, поле электрического заряда.
- 3. Геометрические характеристики скалярного поля - поверхности и линии уровня.
- 4. Линия уровня - геометрическая характеристика плоского поля При помощи геометрических характеристик скалярные поля можно рисовать.
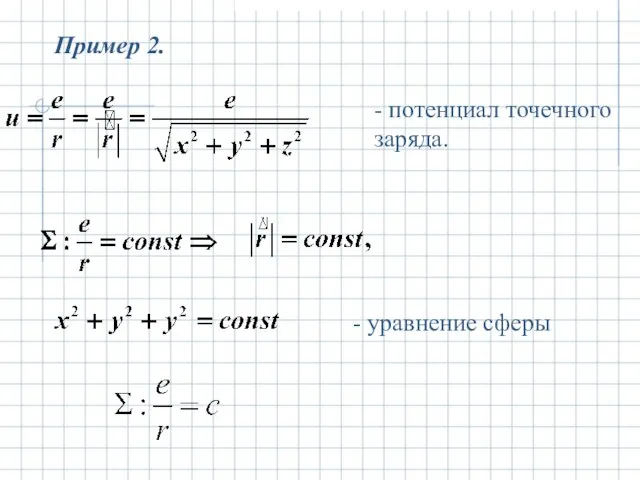
- 5. Пример 2. - потенциал точечного заряда. - уравнение сферы
- 6. характеристики отдельной точки поля. 1. Производная по направлению - скалярная характеристика. Найдем, как изменяется поле в
- 7. где
- 8. Из определения следует: Смысл производной по направлению
- 9. Рассмотрим
- 10. Устремим Рассмотрим *)
- 11. -направляющие косинусы коллинеарных векторов Координаты орта этих векторов:
- 12. Формула для вычисления производной по направлению
- 13. 2. Градиент скалярного поля - векторная характеристика. Смысл характеристики - позже. Формула для вычисления – в
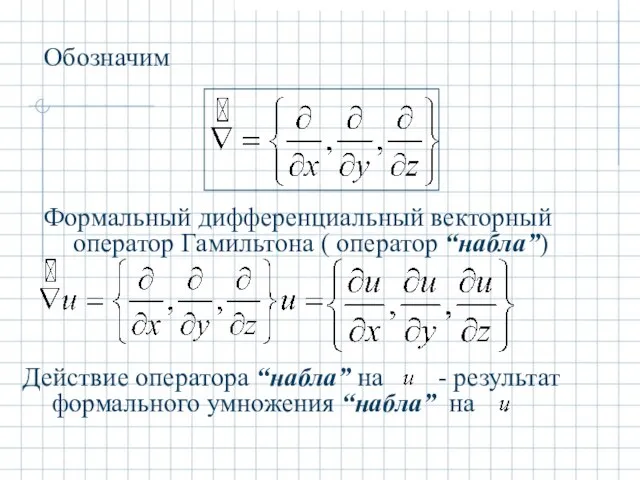
- 14. Обозначим Формальный дифференциальный векторный оператор Гамильтона ( оператор “набла”)
- 15. Свойства оператора “набла” 1. 2. 3. 4.
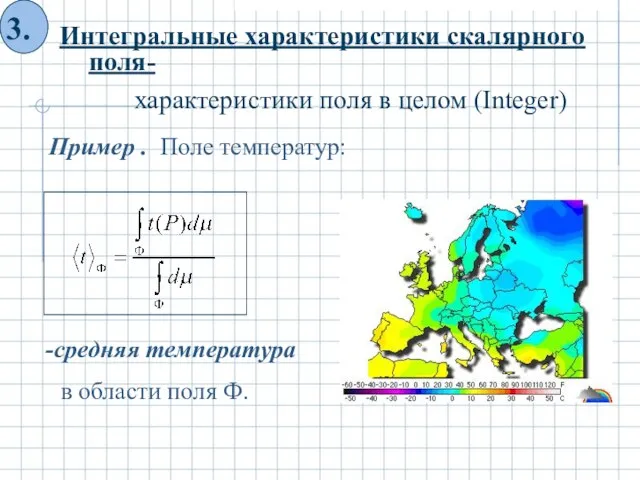
- 16. характеристики поля в целом (Integer) Пример . Поле температур: средняя температура в области поля Ф.
- 17. 1. Градиент и производная по направлению.
- 18. 2. Смысл градиента. Из формулы вычисления градиента следует
- 19. Длина градиента численно равна максимальной скорости возрастания скалярного поля u .
- 20. 3. Градиент и поверхности уровня. Рассмотрим - уравнение поверхности уровня - вектор нормали к касательной плоскости
- 21. Выводы. 1. Градиент направлен по нормали к поверхности уровня. 2. Направление нормали к поверхности уровня есть
- 22. Пример. Решение.
- 24. Скачать презентацию






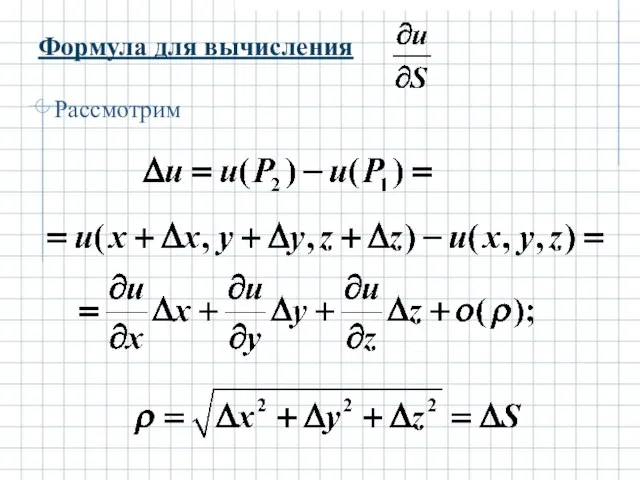











 ставропольская государственная медицинская академия
ставропольская государственная медицинская академия О реализации плана мероприятий по снижению уровня общей безработицы до 7% в разрезе муниципальных образований
О реализации плана мероприятий по снижению уровня общей безработицы до 7% в разрезе муниципальных образований Габдулла Тукай – Величайший татарский поэт
Габдулла Тукай – Величайший татарский поэт Презентация на тему Великие о математике
Презентация на тему Великие о математике  Презентация на тему Европейский Север Факторы формирования района
Презентация на тему Европейский Север Факторы формирования района Социально-экономическое обоснование строительства Перинатального центра
Социально-экономическое обоснование строительства Перинатального центра Источники финансирования проекта
Источники финансирования проекта ProQuest Dissertations and Theses: Крупнейшая полнотекстовая база данных научных диссертаций
ProQuest Dissertations and Theses: Крупнейшая полнотекстовая база данных научных диссертаций Асинхронные машины специального назначения
Асинхронные машины специального назначения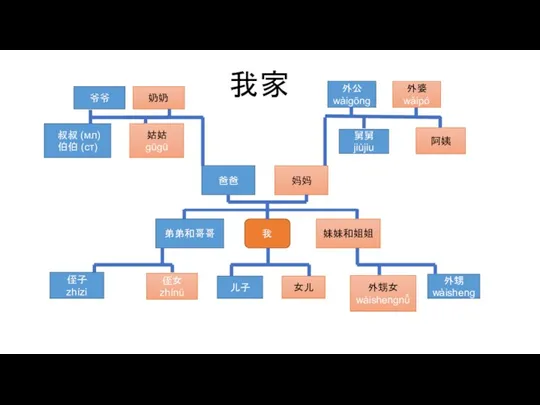 一个家族
一个家族 Промо-программа -30% на смеситель при покупке тумбы
Промо-программа -30% на смеситель при покупке тумбы Абстракціоні́зм, абстрактне мистецтво, безпредметне мистецтво, конфігуративне мистецтво
Абстракціоні́зм, абстрактне мистецтво, безпредметне мистецтво, конфігуративне мистецтво Needs to be updated after tv unit design space planning
Needs to be updated after tv unit design space planning Группы безударных гласных в корне
Группы безударных гласных в корне Виды политических режимов
Виды политических режимов ПРОДВИЖЕНИЕУСЛУГ МТС
ПРОДВИЖЕНИЕУСЛУГ МТС Династический кризис 1825
Династический кризис 1825 Народов дружная семья
Народов дружная семья Учёт особенностей поведения младших школьников в процессе обучения и воспитания
Учёт особенностей поведения младших школьников в процессе обучения и воспитания Презентация на тему 7 чудес России
Презентация на тему 7 чудес России 100 технік масажу
100 технік масажу  Политические партии современной России
Политические партии современной России Методические рекомендации для студентов по подготовке и защите курсовой работы
Методические рекомендации для студентов по подготовке и защите курсовой работы Презентация на тему Деревья леса
Презентация на тему Деревья леса Возможность CorelDRAW X3
Возможность CorelDRAW X3 Интернет-портал «Мобильные новости»Mnovosti.ru
Интернет-портал «Мобильные новости»Mnovosti.ru Альбом ППС 82 км
Альбом ППС 82 км Многогранники в архитектуре
Многогранники в архитектуре