ВЕКТОРЫ

В п.В6 первой части ЕГЭ по математике включены задания по теме «Векторы».
В презентации предложены конечно не все задания, а только которые (на мой взгляд) наиболее полно раскрывают все содержание темы, в их решении использованы основные приемы и формулы, применяемые в других заданиях.
Внимание!

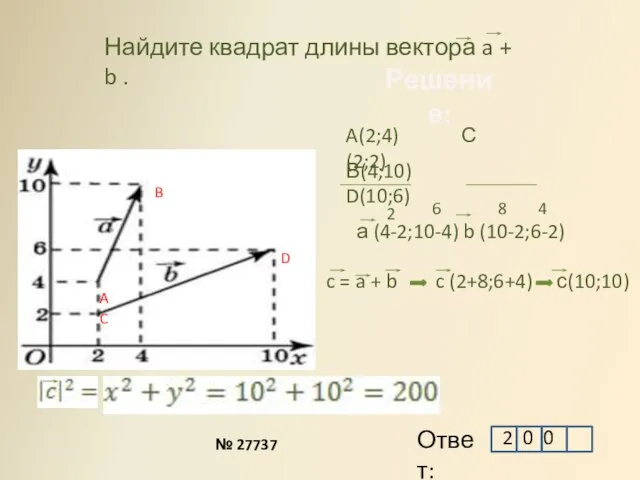
Найдите квадрат длины вектора a + b .
A
B
C
D
A(2;4) С(2;2)
В(4;10) D(10;6)
а (4-2;10-4) b (10-2;6-2)
c = a + b c (2+8;6+4) с(10;10)
Решение:
2 0 0
2
6
8
4
№ 27737

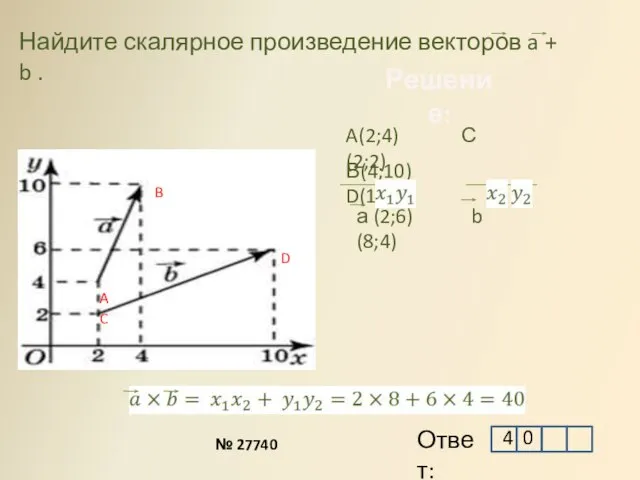
Найдите скалярное произведение векторов a + b .
A
B
C
D
A(2;4) С(2;2)
В(4;10) D(10;6)
а (2;6) b (8;4)
Решение:
4 0
№ 27740

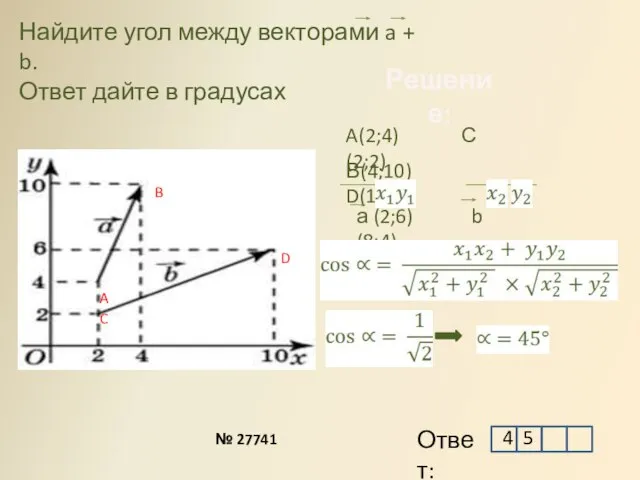
Найдите угол между векторами a + b.
Ответ дайте в градусах
A
B
C
D
A(2;4) С(2;2)
В(4;10) D(10;6)
а (2;6) b (8;4)
Решение:
4 5
№ 27741

Найдите сумму координат вектора a - b .
B
D
B(2;4), D(8;6), а т.к. векторы выходят из начала координат, то
а (2;4) b (8;6)
c = a - b c (2-8;4-6) с(-6;-2)
Решение:
x +y = -6 + (-2) = -8
- 8
С
№ 27732

Вектор AB с концом в точке B(5, 3) имеет координаты
(3, 1). Найдите абсциссу точки A.
B
D
B(5;3), A(x;y), AB(3;1)
Решение:
AB(5-x;3-y), т.е.5-x=3; 3-y=1
x= 2
2
№ 27727

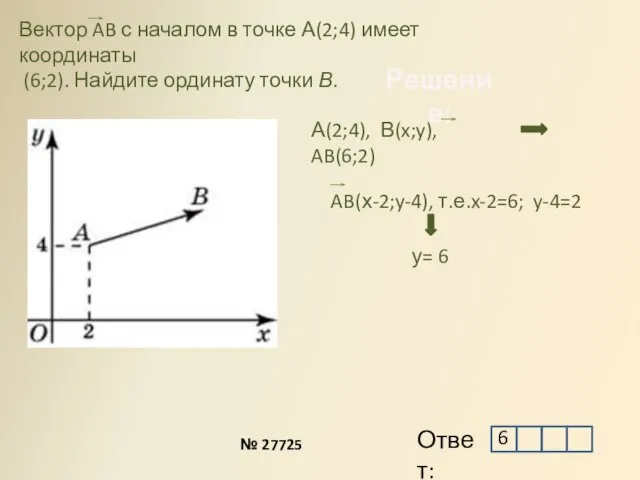
Вектор AB с началом в точке А(2;4) имеет координаты
(6;2). Найдите ординату точки В.
B
D
А(2;4), В(x;y), AB(6;2)
Решение:
AB(х-2;y-4), т.е.x-2=6; y-4=2
у= 6
6
№ 27725

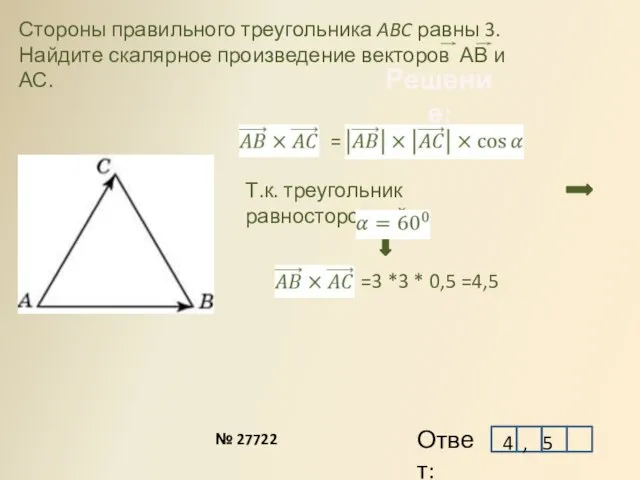
Стороны правильного треугольника ABC равны 3.
Найдите скалярное произведение векторов АВ и АС.
Решение:
=
Т.к. треугольник равносторонний
=3 *3 * 0,5 =4,5
4 , 5
№ 27722

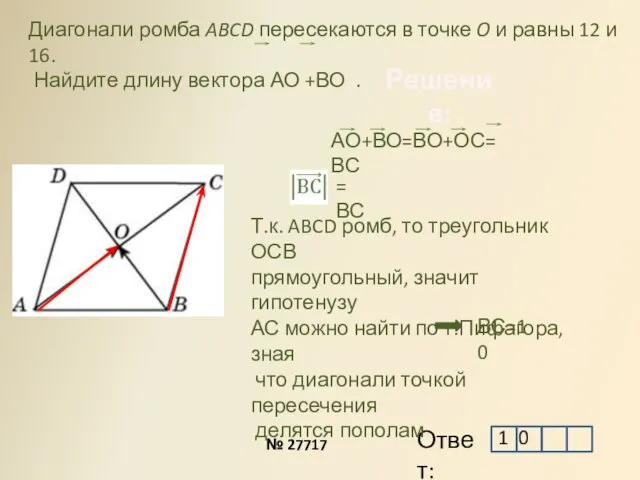
Решение:
АО+ВО=ВО+ОС=ВС
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16.
Найдите длину вектора АО +ВО .
№ 27717
= ВС
Т.к. ABCD ромб, то треугольник ОСВ
прямоугольный, значит гипотенузу
АС можно найти по т.Пифагора, зная
что диагонали точкой пересечения
делятся пополам
ВС=10
1 0

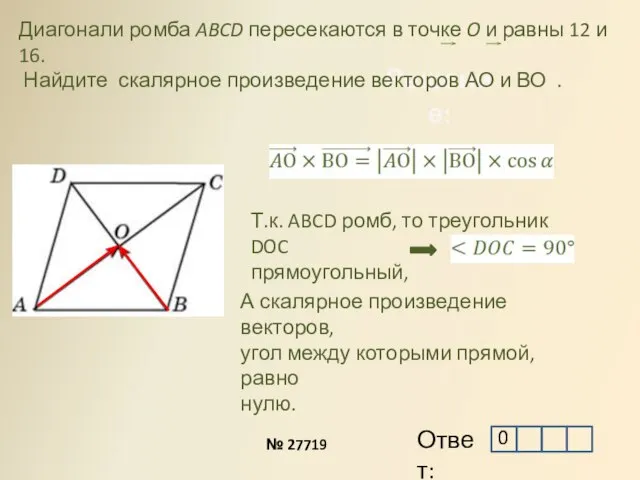
Решение:
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16.
Найдите скалярное произведение векторов АО и ВО .
№ 27719
Т.к. ABCD ромб, то треугольник DOC
прямоугольный,
А скалярное произведение векторов,
угол между которыми прямой, равно
нулю.
0

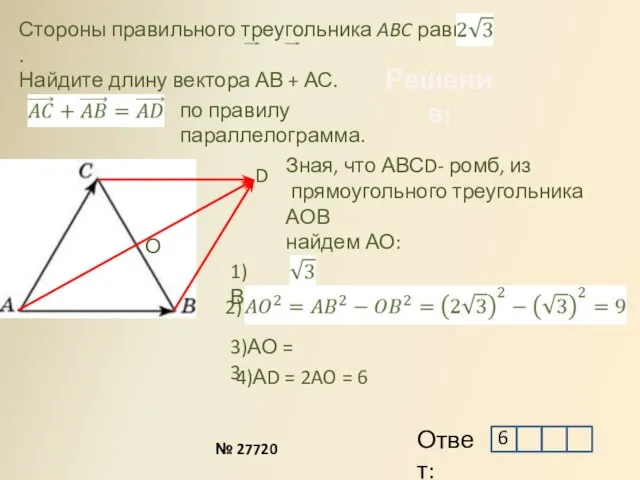
Стороны правильного треугольника ABC равны .
Найдите длину вектора АВ + АС.
Решение:
D
по правилу параллелограмма.
О
Зная, что АВСD- ромб, из
прямоугольного треугольника АОВ
найдем АО:
1) ВО=
2)
3)АО = 3
4)АD = 2AO = 6
6
№ 27720

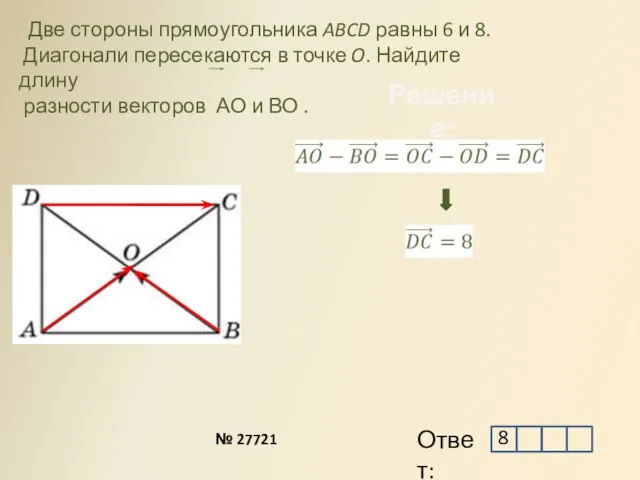
Две стороны прямоугольника ABCD равны 6 и 8.
Диагонали пересекаются в точке O. Найдите длину
разности векторов АО и ВО .
Решение:
№ 27721
8

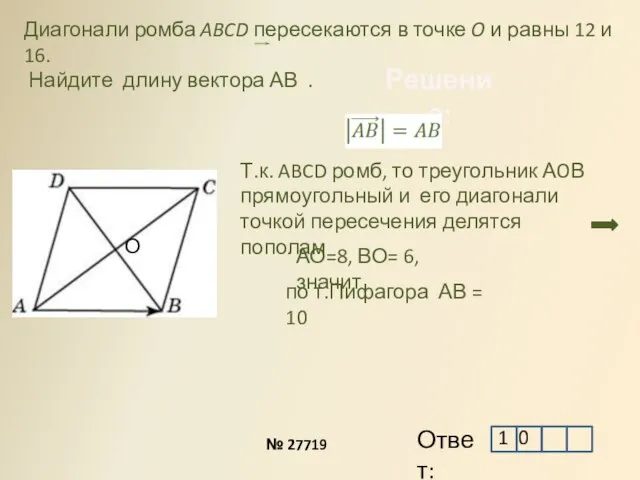
Решение:
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16.
Найдите длину вектора АВ .
№ 27719
Т.к. ABCD ромб, то треугольник АOВ
прямоугольный и его диагонали
точкой пересечения делятся пополам
1 0
О
АО=8, ВО= 6, значит
по т.Пифагора АВ = 10