Векторы в пространстве

Как и в плоскости, в пространстве вектор определяется как направленный отрезок:
A
B
Точка А – начало вектора, В – конец вектора. Записывают: или .
a
Обычную точку в пространстве мы также можем считать вектором, у которого начало совпадает с конечной точкой. Такой вектор называется нулевым и обозначается: или .
A
Длина отрезка, изображающего вектор, называется модулем (или абсолютной величиной) вектора, т.е.
Естественно, что
I. Определение вектора. Основные понятия, связанные с векторами.
A
B
Векторы и являются противоположными. Очевидно, что:

Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых:
a
b
c
Коллинеарные векторы, в свою очередь, бывают одинаково направленными (или соноправленными) и противоположно направленными. В нашем случае:
Обозначение коллинеарных векторов:
– соноправленные векторы, , – противоположно направленные векторы.
m
n
Два вектора называются равными, если: 1) они соноправлены; и 2) их модули равны, т.е.

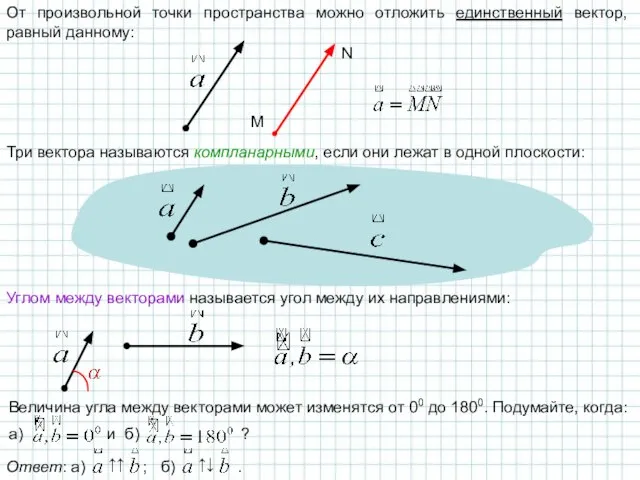
От произвольной точки пространства можно отложить единственный вектор, равный данному:
M
N
Три вектора называются компланарными, если они лежат в одной плоскости:
Углом между векторами называется угол между их направлениями:

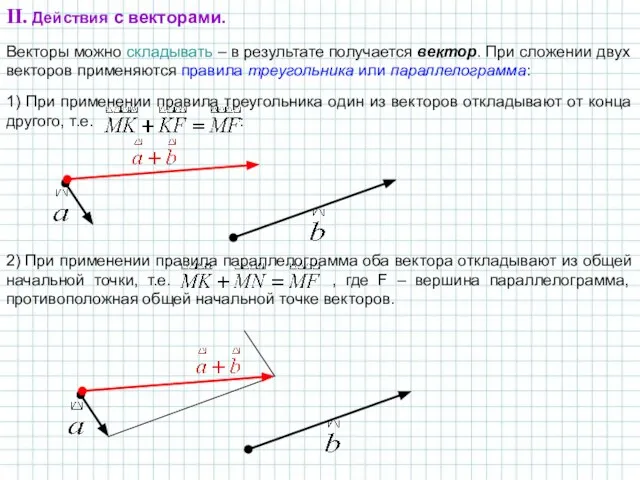
II. Действия с векторами.
Векторы можно складывать – в результате получается вектор. При сложении двух векторов применяются правила треугольника или параллелограмма:
1) При применении правила треугольника один из векторов откладывают от конца другого, т.е. :
2) При применении правила параллелограмма оба вектора откладывают из общей начальной точки, т.е. , где F – вершина параллелограмма, противоположная общей начальной точке векторов.

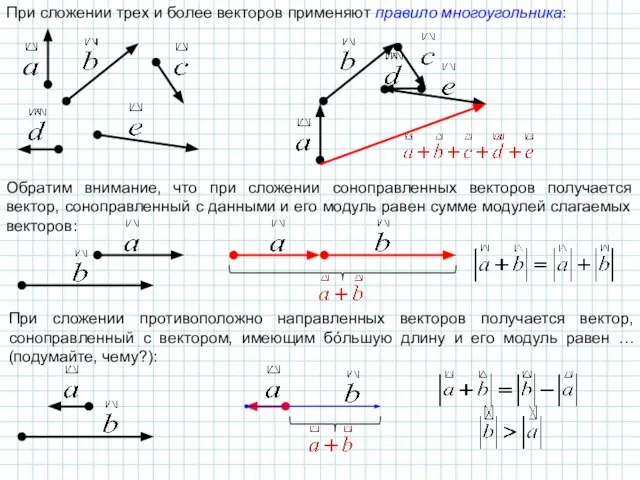
При сложении трех и более векторов применяют правило многоугольника:
Обратим внимание, что при сложении соноправленных векторов получается вектор, соноправленный с данными и его модуль равен сумме модулей слагаемых векторов:
При сложении противоположно направленных векторов получается вектор, соноправленный с вектором, имеющим бóльшую длину и его модуль равен … (подумайте, чему?):

Также можно найти разность двух векторов – в результате получается вектор. При вычитании двух векторов применяется видоизмененное правило треугольника – вначале оба вектора строятся с общей начальной точкой, затем соединяются концы этих векторов с выбором направления к «уменьшаемому» вектору:
–

Сложение векторов, как и сложение чисел подчиняется законам:
Следующее действие с векторами – умножение вектора на число k. В результате этого действия получается вектор, причем:
если k>0, то и ;
если k<0, то и ;
если k=0, то .

И еще одно действие с векторами – умножение двух векторов. В школьном курсе геометрии изучается скалярное произведение векторов. В результате этого действия (в отличии от предыдущих действий с векторами) получается число, равное произведению модулей двух данных векторов на косинус угла между этими векторами, т.е.
Геометрически скалярное произведение векторов можно понимать как площадь параллелограмма (или противоположная ей величина), стороны которого образуются одним из данных векторов и вектором, перпендикулярным второму с таким же модулем:
α – острый угол
α – тупой угол

Теперь рассмотрим все эти понятия и действия с точки зрения координатного пространства. Вспомним, что любая точка пространства задается тремя координатами А(x;y;z).
A(x1;y1;z1)
B(x2;y2;z2)
Если принять вектор за параллельный перенос начальной точки A(x1;y1;z1) в конечную точку B(x2;y2;z2), то координаты вектора показывают: на сколько изменяются соответствующие координаты начальной точки при параллельном переносе в конечную, т.е.
Т.к. модуль вектора равен длине изображающего его отрезка, то:
III. Координаты вектора. Действия в координатах.

Для сложения двух векторов, заданных координатами, нужно просто сложить их соответствующие координаты, т.е.
При вычитании векторов, заданных координатами, нужно найти разности их соответствующих координат, т.е.
Умножение вектора, заданного координатами, на число выполняется так:
Скалярное произведение двух векторов, заданных координатами, равно сумме произведений соответствующих координат, т.е.
Условием коллинеарности двух векторов, заданных координатами, будет пропорциональность их соответствующих координат:
Самостоятельно разберитесь, когда и .

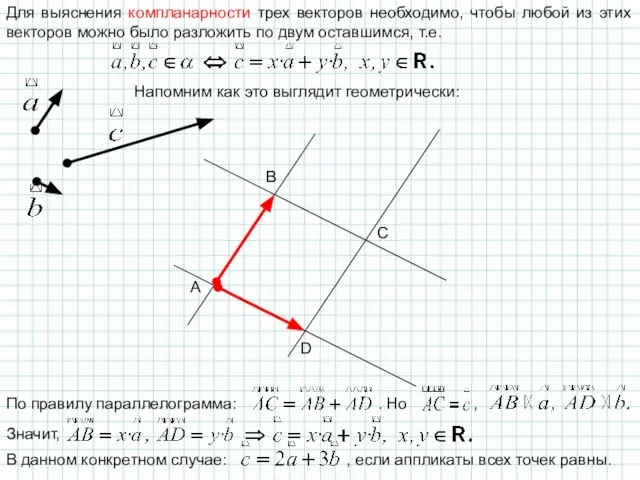
Для выяснения компланарности трех векторов необходимо, чтобы любой из этих векторов можно было разложить по двум оставшимся, т.е.
A
B
C
D
Напомним как это выглядит геометрически:

Аналитически выяснить компланарность трех векторов, заданных координатами, можно решая систему:
Если система имеет единственное решение, то векторы компланарны.
Любой вектор пространства можно разложить по трем некомпланарным векторам, т.е.
Аналитически разложение любого вектора по трем некомпланарным векторам сводится к решению системы:
А решение этой системы – числа x, y и z являются коэффициентами разложения вектора по трем векторам

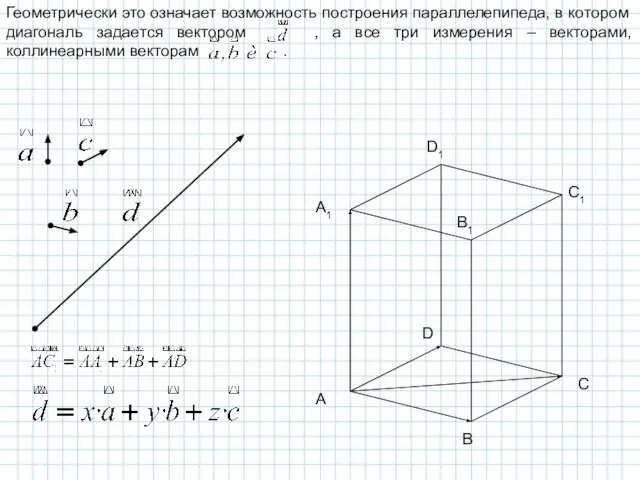
A
B
C
D
A1
B1
C1
D1

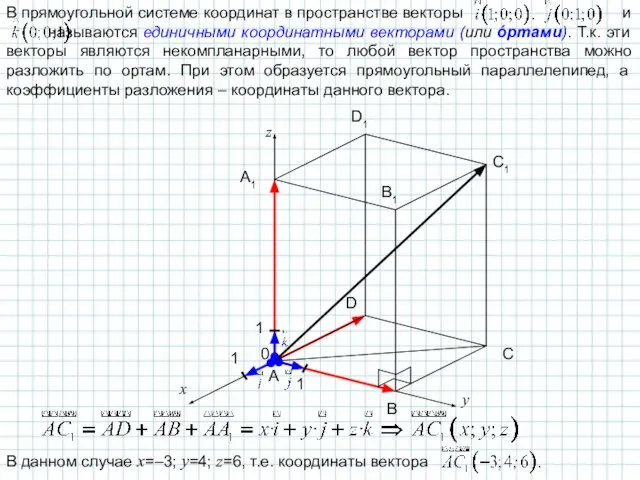
В прямоугольной системе координат в пространстве векторы и называются единичными координатными векторами (или óртами). Т.к. эти векторы являются некомпланарными, то любой вектор пространства можно разложить по ортам. При этом образуется прямоугольный параллелепипед, а коэффициенты разложения – координаты данного вектора.
x
y
z
A
B
C
D
A1
B1
C1
D1
0
1
1
1