Слайд 2Моделирование
упростить и понять реальную ситуацию
проанализировать
разработать прогноз развития
осуществлять управление
X ↔ Y
Ассоциация ≡ связь

x ↔ y
Корреляция ≡ теснота связи
Регрессия ≡ описание связи
x = расходы на рекламу, y = объем продаж
Слайд 5Линейная регрессия
X ↔ Y, пусть y зависит от x: ŷ = f(x)
ŷ

= a + bx
а – пересечение с осью у ; b – угол наклона линии регрессии (коэффициент регрессии)
Ошибка (отклонение, остаток): e = y - ŷ
Линия регрессии ≡ линия наилучшего подбора методом наименьших квадратов : min Σ ei2
Слайд 6Параметры a, b
Нахождение b
Функция НАКЛОН (y; x)
Нахождение a
Функция ОТРЕЗОК (y; x)

Слайд 7Теснота линейной связи
y = y - е
Остаток, разница между фактическим

значением у и значением у на прямой.
Линейная связь только частично объясняет вариации значений у. Необъясненная часть является остатком, е.
Слайд 8Коэффициент детерминации
Общая вариация у: Σ (у -y )2
C учетом линейной связи: Σ

(ŷ -у )2
Не объясняется линейной связью: Σ (y - ŷ)2
Коэффициент детерминации:
Функция КВПИРСОН (y; x)
Слайд 9Интерпретация
r2 выражается в % и показывает величину дисперсии у, которая объясняется

независимой переменной х
в случае полной линейной связи между х и у r2 =1, или 100%
связь отсутствует ⇒ r2 = 0
r2 не определяет, увеличивается ли или уменьшается у с ростом х
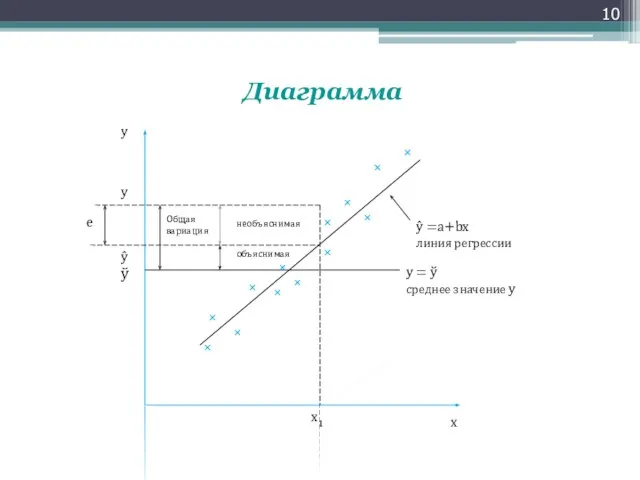
Слайд 10Диаграмма
x1
e
x
y
Общая вариация
необъяснимая
объяснимая
ŷ
y
ŷ =a+bx
линия регрессии
y = ў
среднее значение y
ў
Слайд 11⏐r⏐< 1, знак r совпадает со знаком b
Функция КОРРЕЛ (x; y)
Коэффициент корреляции

Слайд 12 Интерпретация
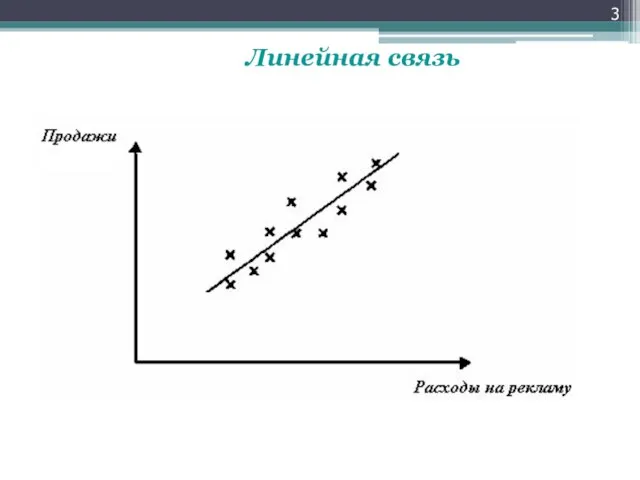
↑ сила линейной связи ⇒ точки на графике ближе к прямой

линии, r ближе к 1
↓ силы связи ⇒ r ближе к 0, точки более рассеяны
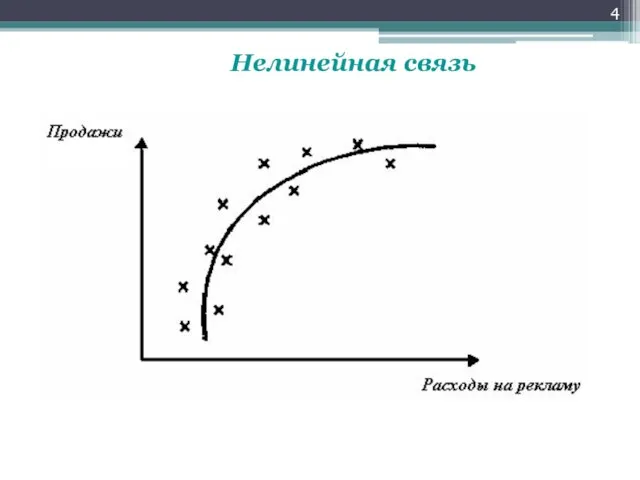
r = 0 ⇒ линейной связи не существует
(не значит, что не существует вообще никакой связи)









 Выход предприятия на Оптовый Рынок Электроэнергии и Мощности (ОРЭМ)
Выход предприятия на Оптовый Рынок Электроэнергии и Мощности (ОРЭМ) Мобильное рабочее место. Приложение для мобильной регистрации клиентов
Мобильное рабочее место. Приложение для мобильной регистрации клиентов Проблемы формирования информационного общества
Проблемы формирования информационного общества 05 - Правоотношения
05 - Правоотношения Генетика человека Элективный курс для учащихся 9 класса
Генетика человека Элективный курс для учащихся 9 класса Сколько стоит интернет-магазин? На чём можно сэкономить.
Сколько стоит интернет-магазин? На чём можно сэкономить. Нормативные модели ППР - функции
Нормативные модели ППР - функции ТЕМА ОДИНОЧЕСТВА В ЛИРИКЕ М.Ю. ЛЕРМОНТОВА
ТЕМА ОДИНОЧЕСТВА В ЛИРИКЕ М.Ю. ЛЕРМОНТОВА Русская природа в музыке и поэзии
Русская природа в музыке и поэзии Презентация на тему Красная книга России
Презентация на тему Красная книга России  Использование метода круговой тренировки для повышения функциональных способностей боксеров
Использование метода круговой тренировки для повышения функциональных способностей боксеров Презентация на тему Реализм
Презентация на тему Реализм Фильм Выход через сувенирную лавку
Фильм Выход через сувенирную лавку Третичный сектор хозяйства
Третичный сектор хозяйства Искусство кино
Искусство кино Толерантность и мы.
Толерантность и мы. Музей Победы и Центр международной торговли
Музей Победы и Центр международной торговли Ориентация спутника в трехмерном пространстве
Ориентация спутника в трехмерном пространстве 4 заседание Совета по Устойчивому Развитию РКАстана, 5 декабря 2007 года Корпоративная социальная ответственность в контексте ус
4 заседание Совета по Устойчивому Развитию РКАстана, 5 декабря 2007 года Корпоративная социальная ответственность в контексте ус Єдиний державний реєстр юридичних осіб, фізичних осіб підприємців та громадських формувань
Єдиний державний реєстр юридичних осіб, фізичних осіб підприємців та громадських формувань 1968 - 2018 ж Ақжар орта мектебінің түлектеріне 50 жыл. Фотоальбом
1968 - 2018 ж Ақжар орта мектебінің түлектеріне 50 жыл. Фотоальбом Презентация на тему Детская одаренность
Презентация на тему Детская одаренность  График квадратичной функции Занятие в 9 классе Продолжительность 40 минут Учитель математики Лещенко Любовь Владимировна в
График квадратичной функции Занятие в 9 классе Продолжительность 40 минут Учитель математики Лещенко Любовь Владимировна в Технические требования. Лист4
Технические требования. Лист4 ФЕДЕРАЛЬНАЯ АНТИМОНОПОЛЬНАЯ СЛУЖБА Москва, 2006 г. Новое правовое поле и новые полномочия ФАС России.
ФЕДЕРАЛЬНАЯ АНТИМОНОПОЛЬНАЯ СЛУЖБА Москва, 2006 г. Новое правовое поле и новые полномочия ФАС России. Презентация на тему Культура поведения и общения
Презентация на тему Культура поведения и общения Презентация на тему Климат России 8 класс
Презентация на тему Климат России 8 класс Старанний і дружний наш 1-Б клас
Старанний і дружний наш 1-Б клас