ВОЛНОВЫЕ СВОЙСТВА МИКРОЧАСТИЦ ВЕЩЕСТВА Гипотеза де Бройля Дифракция

Гипотеза де Бройля
х
В оптических явлениях наблюдается своеобразный дуализм.
Наряду с явлениями дифракции, интерференции (волновыми явлениями) наблюдаются и явления, характеризующие корпускулярную природу света (фотоэффект, эффект Комптона).
В 1924 г. Луи де Бройль выдвинул гипотезу, что дуализм не является особенностью только оптических явлений, а имеет универсальный характер. Частицы вещества также обладают волновыми свойствами.

х
Луи де Бройль (1892 – 1987), французский физик, удостоенный Нобелевской премии 1929 г. по физике за открытие волновой природы электрона. В 1923, распространив идею А.Эйнштейна о двойственной природе
света на вещество, предположил, что поток материальных частиц должен обладать и волновыми свойствами, связанными с их массой и энергией (волны де Бройля). Экспериментальное подтверждение этой идеи было получено в 1927 в опытах по дифракции электронов в кристаллах, а позже она получила практическое применение при разработке магнитных линз для электронного микроскопа. Концепцию де Бройля о корпускулярно-волновом дуализме использовал Э.Шредингер при создании волновой механики.

х
«В оптике, – писал де Бройль, – в течение столетия слишком пренебрегали корпускулярным способом рассмотрения по сравнению с волновым; не делалась ли в теории вещества обратная ошибка?»
Допуская, что частицы вещества наряду с корпускулярными свойствами имеют также и волновые, де Бройль перенес на случай частиц вещества те же правила перехода от одной картины к другой, какие справедливы в случае света.

х
Если фотон обладает энергией E = hv и импульсом p = h/λ, то и частица (например, электрон), движущаяся с некоторой скоростью, обладает волновыми свойствами, т.е. движение частицы можно рассматривать как движение волны.

х
Гипотеза де Бройля была революционной, даже для того революционного в науке времени. Однако, она вскоре была подтверждена многими экспериментами.

х
Дифракция частиц
Дифракция частиц - рассеяние микрочастиц (электронов, нейтронов, атомов и т.п.) кристаллами или молекулами жидкостей и газов, при котором из начального пучка частиц данного типа возникают дополнительно отклонённые пучки этих частиц.
Направление и интенсивность таких отклонённых пучков зависят от строения рассеивающего объекта.

х
Опыты по дифракции частиц и их квантовомеханическая интерпретация.
Первым опытом по дифракции частиц, блестяще подтвердившим исходную идею квантовой механики – корпускулярно-волновой дуализм, явился опыт американских физиков К. Дэвиссона и Л. Джермера проведенный в 1927 по дифракции электронов на монокристаллах никеля. Эти опыты показали, что в определенных условиях электроны проявляют волновые свойства.

х
Ni монокристалл
поток электронов

х
K = eU →
Здесь U выражено в В, а λ – в Å (1 Å = 10–10 м). При напряжениях U порядка 100 В, которые использовались в этих опытах, получаются так называемые «медленные» электроны с λ порядка 1 Å. Эта величина близка к межатомным расстояниям d в кристаллах, которые составляют несколько Å и менее, и соотношение λ ≤ d, необходимое для возникновения дифракции, выполняется.

х
В опыте Дэвиссона и Джермера при «отражении» электронов от поверхности кристалла никеля при определённых углах отражения возникали максимумы.
Волновые свойства частиц – электронов – были доказаны экспериментом.

х
Идея де Бройля о наличии у частиц вещества волновых свойств получила экспериментальное подтверждение, как для заряженных частиц (электронов), так и для нейтральных – нейтронов, атомов и молекул. Также было показано, что обнаружить волновые свойства у макроскопических тел не представляется возможным из-за присущей им малой длины волны.

х
Как известно, интенсивность пропорциональна квадрату амплитуды. Эксперименты по отражению электронов и др. частиц от поверхности показывают, что по некоторым направлениям обнаруживаются максимумы числа отраженных частиц. Это означает, что в указанных направлениях отражается большее число частиц, чем в других направлениях. С волновой точки зрения наличие максимумов в некоторых направлениях означает, что эти направления соответствуют наибольшей интенсивности волн, связанных с отражающимися частицами.
Физический смысл волн де Бройля

х
Интенсивность дебройлевской волны оказывается большей там, где имеется большее число частиц. Другими словами, интенсивность волн де Бройля в данной области пространства определяет число частиц, попавших в эту область. В этом заключается статистическое, вероятностное толкование волн, связанных с движущимися частицами.
Квадрат амплитуды дебройлевской волны в данной точке пространства является мерой вероятности того, что частица находится в этой области.

х
Согласно двойственной корпускулярно-волновой природе частиц вещества, для описания микрочастиц используются то волновые, то корпускулярные представления. Поэтому приписывать им все свойства частиц и все свойства волн нельзя. Естественно, что необходимо внести некоторые ограничения в применении к объектам микромира понятий классической механики.

х
В классической механике состояние материальной точки (классической частицы) определяется заданием значений координат импульса, энергии и т.д. перечисленные величины называются динамическим переменными.
Микрообъекту не могут быть приписаны указанные динамические переменные.
Соотношение неопределенности
Гейзенберга

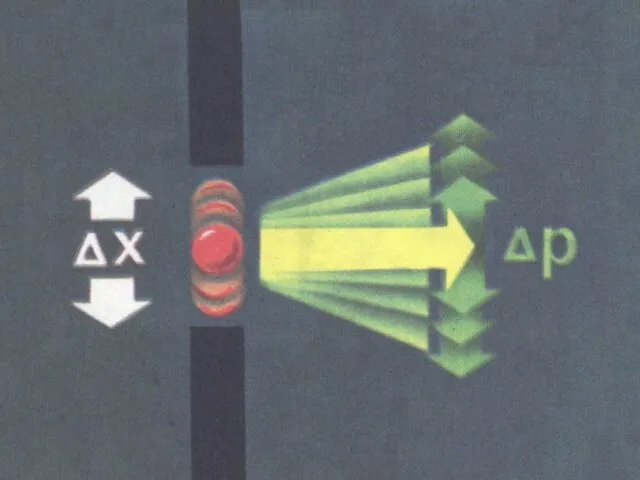
Корпускулярно-волновая двойственность свойств частиц, изучаемых в квантовой механике, приводит к тому, что оказывается невозможным одновременно характеризовать частицу ее положением в пространстве (координатами) и скоростью (или импульсом). Так, например, электрон (и любая другая микрочастица) не может иметь одновременно точных значений координаты x и импульса px. Неопределенности значений x и px удовлетворяют соотношению
х
h – постоянная Планка.

Аналогичное соотношение имеет место для y и py, для z и pz, а также для других пар величин
В классической механике такие пары называются канонически сопряженными:
х
соотношение неопределенности Гейзенберга для величин A и B.
Это соотношение открыл в 1927 году Вернер Гейзенберг.

Соотношение неопределенностей Гейзенберга

Энергия и время являются канонически сопряженными величинами. Поэтому для них также справедливо соотношение неопределенностей
х
это соотношение означает, что определение энергии с точностью ΔE должно занять интервал времени, равный, по меньшей мере

х
Соотношение неопределенностей получено при одновременном использовании классических характеристик движения частицы (координаты, импульса) и наличии у нее волновых свойств.
Т.к. в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то
соотношение неопределенностей является квантовым ограничением применимости классической механике к микрообъектам.

х
Соотношение неопределенностей указывает, в какой мере возможно пользоваться понятиями классической механики применительно к микрочастицам,
в частности, с какой степенью точности можно говорить о траекториях микрочастиц.

х
Понятие о волновой функции
Экспериментальное подтверждение идеи де Бройля об универсальности корпускулярно-волнового дуализма, ограниченность применения классической механики к микрообъектам, диктуемая соотношением неопределенностей, а также противоречия ряда экспериментов с применяемыми в начале XX века теориями привели к новому этапу развития квантовой физики – созданию квантовой механики, описывающей законы движения и взаимодействия микрочастиц с учетом их волновых свойств. Ее создание и развитие охватывает период с 1900 г. (формулировка Планком квантовой гипотезы) до 20-х годов XX века и связано, прежде всего, с работами австрийского физика Э. Шредингера, немецкого физика В. Гейзенберга и английского физика П. Дирака.

х
Необходимость вероятностного подхода к описанию микрочастиц, является важнейшей отличительной особенностью квантовой теории.
Можно ли волны де Бройля истолковывать как волны вероятности, т.е. считать, что вероятность обнаружить микрочастицу в различных точках пространства меняется по волновому закону?
Такое толкование волн де Бройля уже неверно, хотя бы потому, что тогда вероятность обнаружить частицу в некоторых точках пространства может быть отрицательна, что не имеет смысла.

х
Чтобы устранить эти трудности немецкий физик М. Борн в 1926 г. предположил, что по волновому закону меняется не сама вероятность, а величина, названная амплитудой вероятности и обозначаемая
Ψ(х, y, z, t).
Эту величину называют также волновой функцией (или Ψ – функцией).
Амплитуда вероятности может быть комплексной, и вероятность W пропорциональна квадрату ее модуля:
(5)
где |Ψ|2=ΨΨ` , где Ψ` – функция комплексно-сопряженная с Ψ.

х
Таким образом, описание микрообъекта с помощью волновой функции имеет статистический, вероятностный характер:
квадрат модуля волновой функции (квадрат модуля амплитуды волн де Бройля) определяет вероятность нахождения частицы в момент времени в области с координатами x и dx, y и dy, z и dz.

х
Итак, в квантовой механике состояние частицы описывается принципиально по-новому –
с помощью волновой функции, которая является основным носителем информации об их корпускулярных и волновых свойствах. Вероятность нахождения частицы в объеме V равна:
(6)

х
Величина |Ψ2|=dW/dV (квадрат модуля Ψ – функции) имеет смысл плотности вероятности, т.е. определяет вероятность нахождения частицы в единице объема в окрестности точки, имеющей x, y, z.
Таким образом, физический смысл имеет не сама Ψ – функция, а квадрат ее модуля |Ψ2|, которым определяется интенсивность волн де Бройля.

Вероятность найти частицу в момент времени t в конечном объеме V, согласно теореме о сложении вероятностей, равна
х
Т.к. |Ψ|2dυ определяется как вероятность, то необходимо волновую функцию Ψ представить так, чтобы вероятность достоверного события обращалась в единицу, если за объем V принять бесконечный объем всего пространства.
Это означает, что при данном условии частица должна находиться где-то в пространстве.
Условия нормировки вероятностей:

х
(7)
где данный интеграл вычисляется по всему бесконечному пространству, т.е. по координатам x, y, z от –∞ до ∞.
Таким образом, условие нормировки говорит об объективном существовании частицы во времени и пространстве.
Условия нормировки вероятностей:

Условие нормировки волновой функции:

Ну и что ?
Какая польза нам от знания волновой функции?

Чтобы волновая функция являлась объективной характеристикой состояния микрочастицы, она должна удовлетворять ряду ограничительных условий.
Функция Ψ, характеризующая вероятность обнаружить действия микрочастицы в элементе объема, должна быть:
конечной (вероятность не может быть больше единицы);
однозначной (вероятность не может быть неоднозначной величиной);
непрерывной (вероятность не может меняться скачком).
х

х
Волновая функция удовлетворяет принципу суперпозиции: если система может находиться в различных состояниях, описываемых волновыми функциями Ψ1, Ψ2, … Ψn, то она может находиться в состоянии, описываемом линейной комбинацией этих функций
где Cn (n = 1, 2, 3…) – произвольные, комплексные числа.

х
Сложение волновых функций (амплитуд вероятностей определяемых квадратами модулей волновых функций) принципиально отличает квантовую теорию от классической статической теории, в которой для независимых событий справедлива теорема сложения вероятностей.

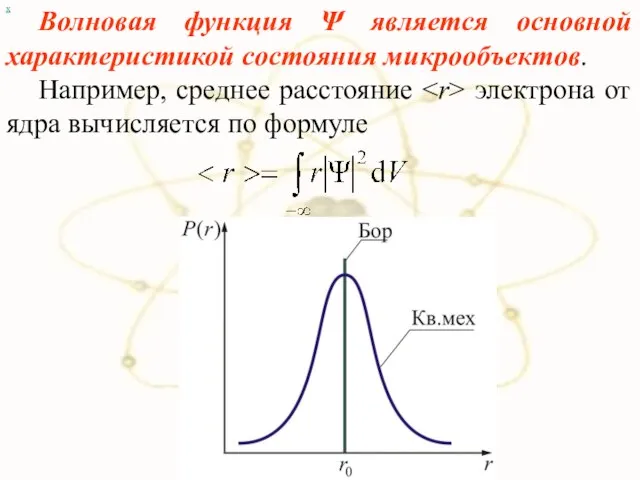
х
Волновая функция Ψ является основной характеристикой состояния микрообъектов.
Например, среднее расстояние электрона от ядра вычисляется по формуле

х
Уравнение Шредингера
Толкование волн де Бройля и соотношение неопределенностей Гейзенберга привели к выводу, что уравнением движения в квантовой механике, описывающей движение микрочастиц в различных силовых полях, должно быть уравнение, из которого бы вытекали наблюдаемые на опыте волновые свойства частиц.

х
Основное уравнение должно быть уравнением относительно волновой функции Ψ(х, y, z, t), т.к. именно величина |Ψ|2, осуществляет вероятность пребывания частицы в момент времени t в объеме dV, т.е. в области с координатами x и x+dx, y, и y+dy, z и z+dz.
Т.к. искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть волновым уравнением, подобно уравнению, описывающему электромагнитные волны.
Основное уравнение нерелятивистской квантовой механики сформулировано в 1926 г. Э.Шредингером.

х
Шредингер Эрвин (1887 – 1961) – австрийский физик-теоретик, один из создателей квантовой механики. Основные работы в области статистической физики, квантовой теории, квантовой механики, общей теории относительности, биофизики.
Разработал теорию движения микрочастиц – волновую механику, построил квантовую теорию возмущений – приближенный метод в квантовой механике. За создание волновой механики удостоен Нобелевской премии.

х
Уравнение Шредингера не выводится, а постулируется.
Правильность этого уравнения подтверждается согласием с опытом получаемых с его помощью результатов, что в свою очередь, придает ему характер закона природы.

х
Уравнение Шредингера в общем виде записывается так:
где
m – масса частицы,
– оператор Лапласа
i2 – мнимая единица,
U(x, y, z, t) – потенциальная энергия частицы в силовом поле, в котором она движется,
Ψ – искомая волновая функция.

х
Если силовое поле, в котором движется частица потенциально, то функция U не зависит явно от времени и имеет смысл потенциальной энергии.
В этом случае решение уравнения Шредингера распадается на два сомножителя, один из которых зависит только от координаты, а другой – только от времени.
Здесь E – полная энергия частицы, которая в случае стационарного поля остается постоянной.

х
Уравнение Шредингера для стационарных состояний
(10)

х
Уравнение Шредингера можно записать в виде
Гамильтониан является оператором энергии E. – оператор Гамильтона, равный сумме операторов
В этом уравнении

х
В квантовой механике другим динамическим переменным сопоставляются операторы. Соответственно рассматривают операторы координат, импульса, момента импульса и т.д.

Эрвин Шрёдингер (1887-1961)
Любое движение
микрочастиц можно
уподобить движению
особых волн