Волновые уравнения Максвелла

При помощи волновой теории объясняются законы распространения света (отражение, преломление, интерференция, дифракция)
при помощи фотонной теории объясняются законы взаимодействия между светом и веществом (поглощение и рассеяние света электронами, излучение и поглощение света атомами)
именно в оптике впервые наблюдается своеобразный дуализм волновых и корпускулярных свойств, который наиболее ярко проявляется в атомной и ядерной физике.
волновая
корпускулярная
природа света

Волновые уравнения
Максвелла

В 1860 г. знаменитый английский физик Джеймс Клерк Максвелл создал единую теорию электрических и магнитных явлений, в которой он использовал понятие ток смещения, дал определение электромагнитного поля (ЭМП) и предсказал существование в свободном пространстве электромагнитного излучения, которое распространяется со скоростью света.
Теорию ЭМП Максвелл сформулировал в виде системы нескольких уравнений. В учении об электромагнетизме эти уравнения Максвелла играют такую же роль, как уравнения (или законы) Ньютона в механике или I и II начала в термодинамике.
(1831-1879) английский физик, создатель классической электродинамики, один из основоположников статистической физики.
Джеймс Клерк Максвелл

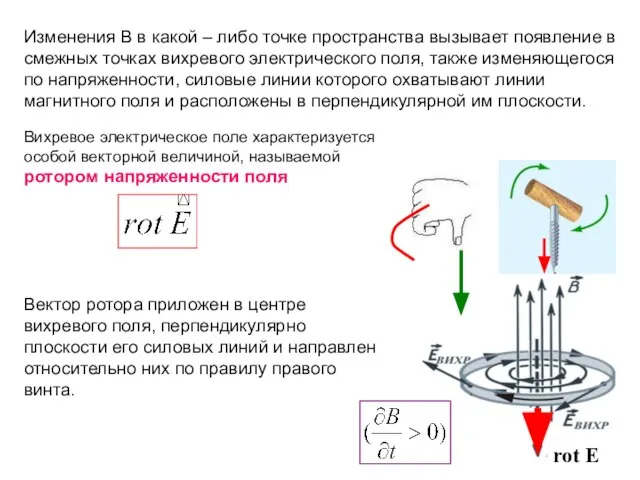
Изменения В в какой – либо точке пространства вызывает появление в смежных точках вихревого электрического поля, также изменяющегося по напряженности, силовые линии которого охватывают линии магнитного поля и расположены в перпендикулярной им плоскости.
Вихревое электрическое поле характеризуется особой векторной величиной, называемой ротором напряженности поля
Вектор ротора приложен в центре вихревого поля, перпендикулярно плоскости его силовых линий и направлен относительно них по правилу правого винта.

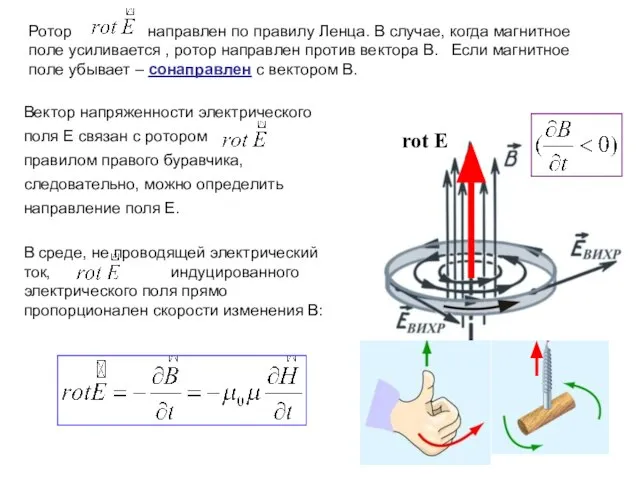
Ротор направлен по правилу Ленца. В случае, когда магнитное поле усиливается , ротор направлен против вектора В. Если магнитное поле убывает – сонаправлен с вектором В.
Вектор напряженности электрического поля Е связан с ротором
правилом правого буравчика, следовательно, можно определить направление поля Е.
В среде, не проводящей электрический ток, индуцированного электрического поля прямо пропорционален скорости изменения В:

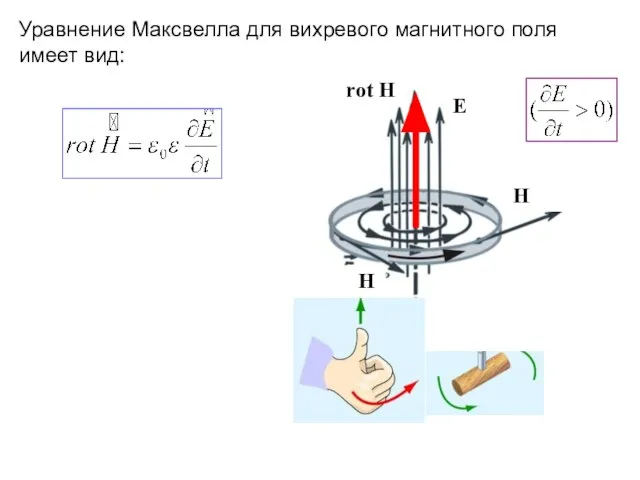
Уравнение Максвелла для вихревого магнитного поля имеет вид:

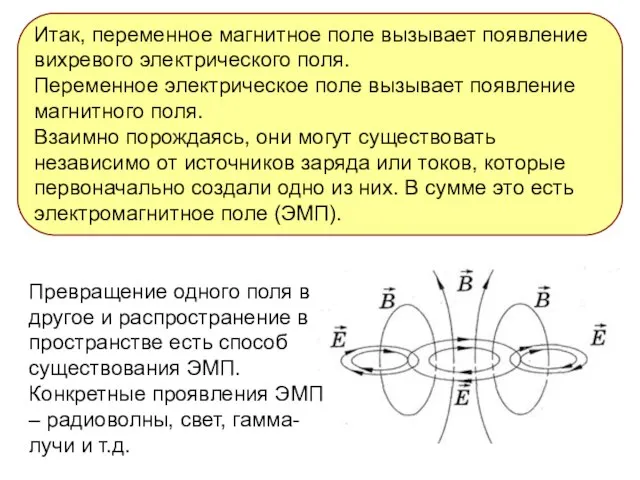
Превращение одного поля в другое и распространение в пространстве есть способ существования ЭМП.
Конкретные проявления ЭМП – радиоволны, свет, гамма-лучи и т.д.
Итак, переменное магнитное поле вызывает появление вихревого электрического поля.
Переменное электрическое поле вызывает появление магнитного поля.
Взаимно порождаясь, они могут существовать независимо от источников заряда или токов, которые первоначально создали одно из них. В сумме это есть электромагнитное поле (ЭМП).

Электромагнитное поле как следствие принципа относительности Энштейна.
Принцип относительности (П.О.) Эйнштейна (сформулирован на основе опыта Майкельсона, Физо и др.):
законы всех физических явлений, в том числе и электромагнитных, имеют одинаковый вид (т.е. описываются одинаковыми уравнениями) во всех инерциальных системах отсчета.

Основные положения теории электромагнитных явлений записываются в виде системы уравнений – уравнения Максвелла. В электромагнетизме эти уравнения играют такую же роль, как законы Ньютона в механике или
I и II начала в термодинамике.
Первое из этих уравнений является выражением закона электромагнитной индукции.
Второе уравнение отражает свойство замкнутости линий вектора (или уход их в бесконечность) или отсутствие источников магнитного поля, т.е. магнитных зарядов.
Первая пара уравнений:
Вторая пара уравнений:
уравнение устанавливает связь между полным током и порождаемым им магнитным полем.
уравнение показывает, что источниками вектора служат сторонние заряды.
уравнения Максвелла в дифференциальной форме

Уравнение электромагнитной волны
Электромагнитное поле не стоит на месте, а распространяется в пространстве. Этот процесс является периодическим и носит волновой характер.
На основе уравнений Максвелла можно получить волновое уравнение э/м волны:
уравнения Максвелла для плоской гармонической
электромагнитной волны, когда токи и заряды отсутствуют
Решение этих уравнений и составляют искомое уравнение волны
Дифференцируя (1) по х и (2) по t, получаем:

Аналогично дифференцируем (1) по t и (2) по х:
Это общее дифференциальное уравнение волны
Если изменение величины S отвечает уравнениям:
то это означает, что величина S распространяется в виде волны со скоростью v.

Таким образом, можно написать:
Дифференциальное уравнение плоской гармонической электромагнитной волны

Фазовая скорость ЭМВ (скорость распространения
фиксированной фазы) определяется выражением
где
– электродинамическая постоянная =
скорости света в вакууме;
В любом веществе скорость распространения электромагнитных возмущений меньше в
раз, чем в вакууме.

Скорость распространения электромагнитных волн в среде зависит от ее электрической и магнитной проницаемостей. Величину называют
абсолютным показателем преломления. С учетом последнего имеем:
и
Следовательно, показатель преломления среды есть физическая величина, равная отношению скорости электромагнитных волн в вакууме к их скорости в данной среде.

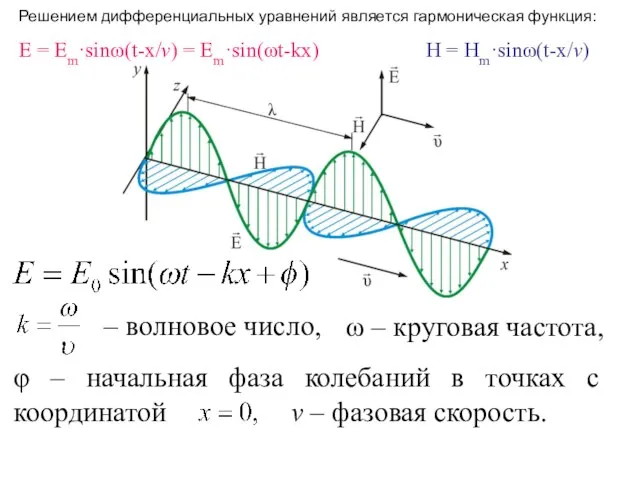
ω – круговая частота,
φ – начальная фаза колебаний в точках с координатой
– волновое число,
v – фазовая скорость.
E = Em·sinω(t-x/v) = Em·sin(ωt-kx) H = Hm·sinω(t-x/v)
Решением дифференциальных уравнений является гармоническая функция:

Таким образом:
• векторы
взаимно перпендикулярны, т. к.
и
направлены одинаково;
• электромагнитная волна является поперечной;
• электрическая и магнитная составляющие распространяются в одном направлении;
колеблются в одинаковых фазах.
• векторы
√εа·E = √μа·H (√ε√ε0·E = √μ√μ0·H)
и их величины связаны соотношением.
и

Энергия электромагнитного поля.
Энергия электромагнитного поля складывается из энергии его электрической и магнитной составляющих. Так как колебания векторов и происходят в фазе, для мгновенных значений объемной плотности энергии электромагнитного поля получаем:
или
(масса единичного объема электромагнитного поля равна w =mc2, a m = w/c2).
Модуль плотности потока энергии волны можно получить, умножив объемную плотность энергии на скорость волны v:
Плотность потока энергии –это вектор, совпадающий с направлением вектора скорости волны, т.е. перпендикулярный векторам Е и Н.

Средняя за период плотность потока энергии, или интенсивность I волны (для плоской э/м волны) численно равна среднему значению за период модуля U
Т.е.
В случае электромагнитных волн вектор плотности потока энергии называется вектором Умова-Пойнтинга. Его можно представить как векторное произведение
√εа·E = √μа·H (√ε√ε0·E = √μ√μ0·H)

Длина волны связана с периодом Т (или частотой ν=1/Т) колебаний:
в вакууме
В соответствии с условиями возбуждения и свойствами излучения ЭМ волны делятся по частоте (или длине волны) на несколько диапазонов, составляющих шкалу ЭМ волн: радиоволны, оптическое излучение, рентгеновское излучение, γ- излучение.
Частоты видимых световых волн лежат в пределах: λ = 760 – 380 нм. Действуя на глаз, видимое излучение вызывает ощущение света.
Излучение может быть
Монохроматическим (простым) называют излучение какой-либо одной длины волны.
Сложным - излучение, состоящее из волн различной длины, называется
Любой цвет можно разложить на сумму основных (или базовых) 3 цветов : красный, зеленый, синий соответствующей яркости
Свет, содержащий все волны видимого диапазона в определенном соотношении по интенсивности – белый свет.

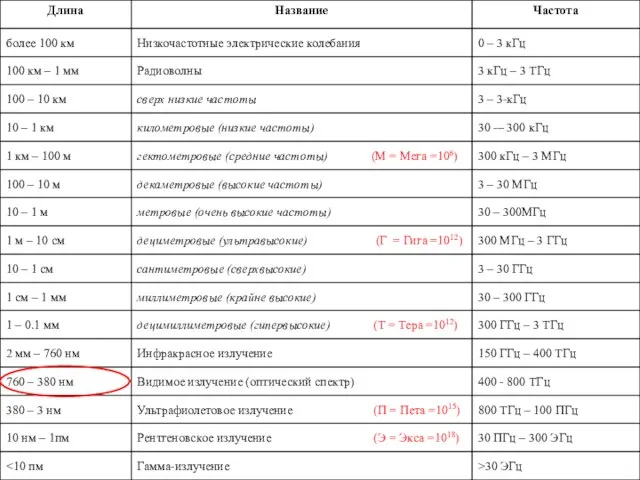
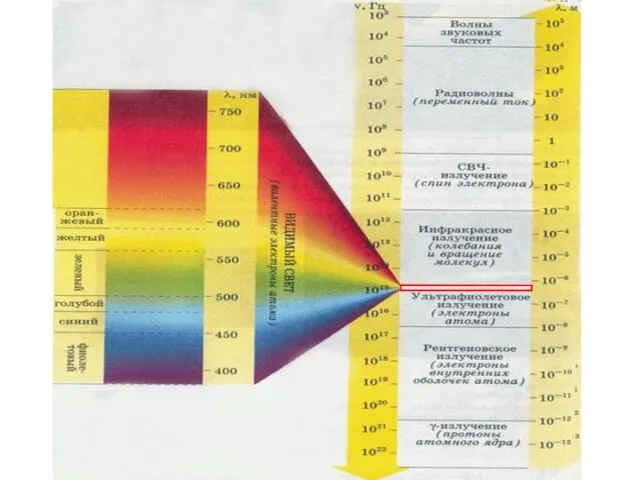
Шкала ЭМВ
В оптике условно рассматривается три области:
Длина волны (λ) < размеров приборов;
геометрическая оптика.
λ сравнима с размеров приборов;
волновая оптика.
λ < размеров приборов;
квантовая оптика.

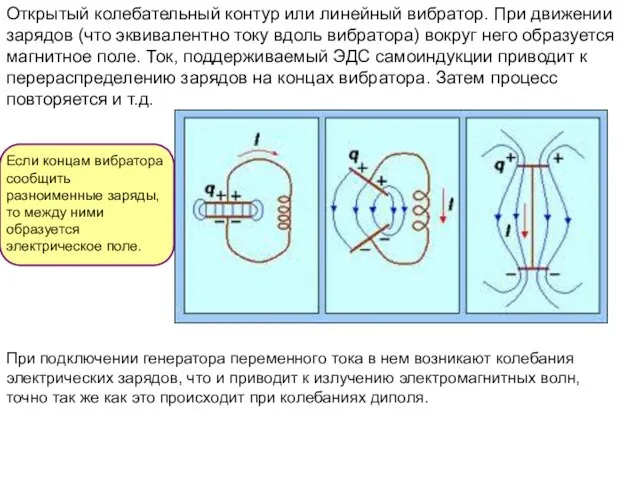
Открытый колебательный контур или линейный вибратор. При движении зарядов (что эквивалентно току вдоль вибратора) вокруг него образуется магнитное поле. Ток, поддерживаемый ЭДС самоиндукции приводит к перераспределению зарядов на концах вибратора. Затем процесс повторяется и т.д.
Если концам вибратора сообщить разноименные заряды, то между ними образуется электрическое поле.
При подключении генератора переменного тока в нем возникают колебания электрических зарядов, что и приводит к излучению электромагнитных волн, точно так же как это происходит при колебаниях диполя.

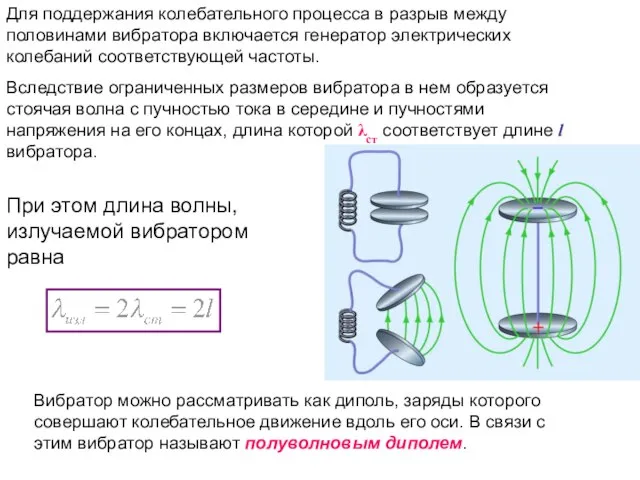
Для поддержания колебательного процесса в разрыв между половинами вибратора включается генератор электрических колебаний соответствующей частоты.
Вследствие ограниченных размеров вибратора в нем образуется стоячая волна с пучностью тока в середине и пучностями напряжения на его концах, длина которой λст соответствует длине l вибратора.
При этом длина волны, излучаемой вибратором равна
Вибратор можно рассматривать как диполь, заряды которого совершают колебательное движение вдоль его оси. В связи с этим вибратор называют полуволновым диполем.

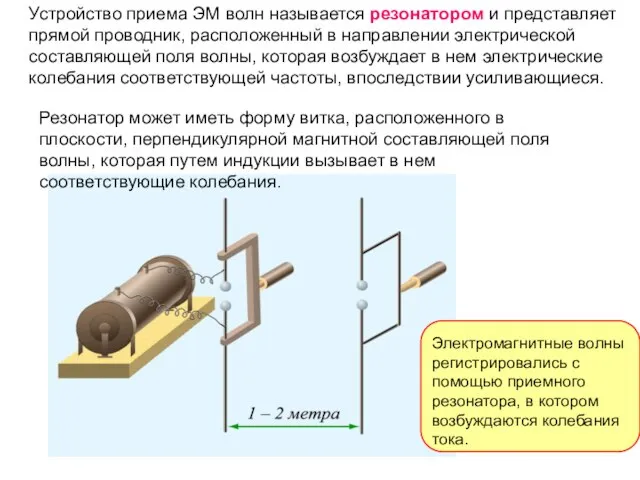
Устройство приема ЭМ волн называется резонатором и представляет прямой проводник, расположенный в направлении электрической составляющей поля волны, которая возбуждает в нем электрические колебания соответствующей частоты, впоследствии усиливающиеся.
Электромагнитные волны регистрировались с помощью приемного резонатора, в котором возбуждаются колебания тока.
Резонатор может иметь форму витка, расположенного в плоскости, перпендикулярной магнитной составляющей поля волны, которая путем индукции вызывает в нем соответствующие колебания.

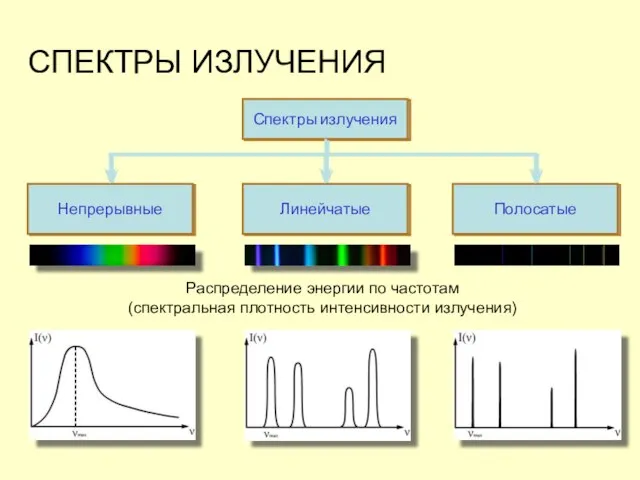
СПЕКТРЫ ИЗЛУЧЕНИЯ
Распределение энергии по частотам
(спектральная плотность интенсивности излучения)

НЕПРЕРЫВНЫЙ СПЕКТР
Дают тела, находящиеся в твердом, жидком состоянии, а также плотные газы.
Чтобы получить, надо нагреть тело до высокой температуры.
Характер спектра зависит не только от свойств отдельных излучающих атомов, но и от взаимодействия атомов друг с другом.
В спектре представлены волны всех длин и нет разрывов.
Непрерывный спектр цветов можно наблюдать на дифракционной решетке. Хорошей демонстрацией спектра является природное явление радуги.

ЛИНЕЙЧАТЫЙ СПЕКТР
Дают все вещества в газообразном атомарном (но не молекулярном) состоянии (атомы практически не взаимодействуют друг с другом).
Изолированные атомы данного химического элемента излучают волны строго определенной длины, называемых спектральными линиями.
Для наблюдения используют свечение паров вещества в пламени или свечение газового разряда в трубке, наполненной исследуемым газом.
При увеличении плотности атомарного газа отдельные спектральные линии расширяются.
Установлено, что в состоянии разреженного газа каждое вещество испускает характерный для него спектр. Благодаря этому возможен спектральный анализ (определение химического состава вещества по спектру излучения этого вещества в газообразном состоянии).

ПОЛОСАТЫЙ СПЕКТР
Спектр состоит из отдельных полос, разделенных темными промежутками.
Каждая полоса представляет собой совокупность большого числа очень тесно расположенных линий.
Создаются молекулами, не связанными или слабосвязанными друг с другом.
Для наблюдения используют свечение паров в пламени или свечение газового разряда.