Волшебный квадрат 9 класс

-рассказать об истории развития магических квадратов,
-рассмотреть свойства магического квадрата 4-ого порядка
-уметь составлять магический квадрат 4-ого порядка
-осветить актуальность магических квадратов в мире, в котором мы живём.
ЦЕЛЬ РАБОТЫ:

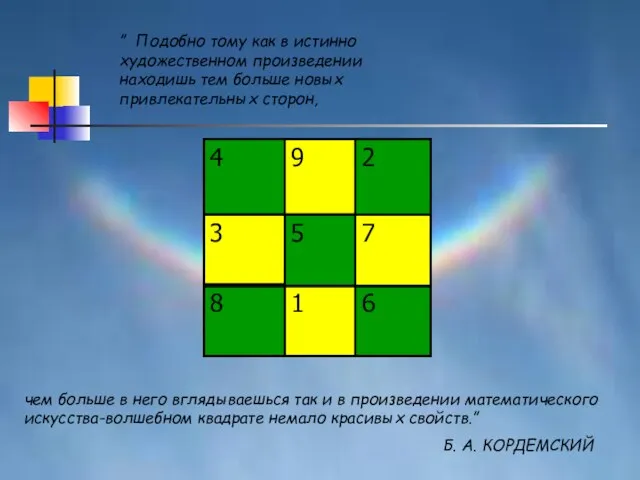
” Подобно тому как в истинно художественном произведении находишь тем больше новых привлекательных сторон,
чем больше в него вглядываешься так и в произведении математического искусства-волшебном квадрате немало красивых свойств.”
Б. А. КОРДЕМСКИЙ

Магический, или волшебный квадрат — это квадратная таблица , заполненная n² числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Если в квадрате равны суммы чисел только в строках и столбцах, то он называется полумагическим. Нормальным называется магический квадрат, заполненный целыми числами от 1 до n².

Каждый элемент магического квадрата называется клеткой. Квадрат, сторона которого состоит из n клеток, содержит n² клеток и называется квадратом n-го порядка. В 16 в. Корнелий Генрих Агриппа построил квадраты 3-го, 4-го, 5-го, 6-го, 7-го, 8-го и 9-го порядков, которые были связаны с астрологией 7 планет. В 19 и 20 вв. интерес к магическим квадратам вспыхнул с новой силой. Их стали исследовать с помощью методов высшей алгебры и операционного исчисления.

Полного описания всех возможных магических квадратов не получено и до сего времени
Известно, что магических квадратов 2х2 не существует. Магических квадратов 3х3 – один – остальные такие квадраты получаются из него поворотами и симметриями. Расположить натуральные числа от 1 до 9 в магический квадрат 3х3 можно 8 различными способами.
Магических квадратов 4х4 уже более 800, а количество магических квадратов 5х5 близко к четверти миллиона.

Придуманы волшебные квадраты впервые, по-видимому, китайцами, так как самое раннее упоминание о них встречались в китайской книге, написанной за 4000-5000 лет до н. э.
Пришельцы из Китая и Индии
Старейший в мире волшебный квадрат это квадрат китайцев .На рисунке чёрными кружками в этом квадрате изображены чётные (женственные) числа, белыми-нечётные (мужественные) числа.

ЛО-ШУ
Согласно легенде, во времена правления императора Ю (ок. 2200 до н.э.) из вод Хуанхэ (Желтой реки) всплыла священная черепаха, на панцире которой были начертаны таинственные иероглифы, и эти знаки известны под названием ло-шу

Латинским квадратом называется квадрат n*n клеток, в которых написаны числа от 1, до n, притом так, что в каждой строке и каждом столбце встречаются все эти числа по одному разу.
Латинские квадраты

В 11 в. о магических квадратах узнали в Индии, а затем в Японии, где в 16 в. магическим квадратам была посвящена обширная литература. Европейцев с магическими квадратами познакомил в 15 в. византийский писатель Э.Мосхопулос. Первым квадратом, придуманным европейцем, считается квадрат А.Дюрера, изображенный на его знаменитой гравюре Меланхолия I. Любопытно, что два числа в середине нижней строки указывают год создания картины-1514.

Самый ранний уникальный магический квадрат, обнаруженный в надписи XI века в индийском городе Кхаджурахо был 4х4. И поэтому рассмотрим свойства волшебного квадрата именно такого размера, как 4х4.

Сумма чисел, расположенных по углам нашего волшебного квадрата, равна 34, т. е. тому же числу, что и сумма чисел вдоль каждого ряда квадрата
1 СВОЙСТВО
2 СВОЙСТВО
Суммы чисел в каждом из маленьких квадратов (в 4 клетки), примыкающих к вершинам данного квадрата, и в таком же центральном квадрате тоже одинаковы и каждая из них равна 34:
1+14+12+7=34
11+13+2+8=34
10+5+3+16=34
15+4+6+9=34
7+6+11+10=34

В каждой строке есть пара рядом стоящих чисел, сумма которых 15, и ещё пара тоже рядом стоящих чисел, сумма которых 19.
3 СВОЙСТВО
4 свойство
Подсчитаем теперь сумму квадратов чисел отдельно в двух крайних строках и двух средних:
Как видите получились попарно равные суммы!

Суммы квадратов чисел двух крайних столбцов равны между собой и суммы квадратов чисел двух средних столбцов тоже одинаковы
5 СВОЙСТВО
6 СВОЙСТВО
Если в данный квадрат вписать ещё один квадрат с вершинами в серединах сторон данного квадрата, то следует ожидать следующее:

равна сумме чисел, расположенных вдоль другой пары противоположных его сторон и каждая из этих сумм равна опять-таки числу 34:
12+14+3+5=15+9+8+2
Сумма чисел, расположенных вдоль одной пары противоположных сторон вписанного квадрата,
а)

Ещё интереснее то, что равны между собой даже суммы квадратов и суммы кубов этих чисел:
б)
При обмене местами отдельных строк или столбцов волшебного квадрата некоторые из вышеперечисленных его свойств могут исчезнуть, но могут и все сохраниться и даже появиться новые. Например, поменяем местами 1 и 2 строку данного квадрата.

Суммы чисел вдоль строк и столбцов, конечно, не изменились, но суммы чисел по диагоналям стали иными, не равными 34. волшебный квадрат потерял часть своих основных свойств, стал «неполным волшебным квадратом».
12
1
8
13
7
14
11
2
6
15
10
3
9
4
5
16
Продолжая обменивать местами строки и столбцы квадрата, мы будем получать всё новые и новые волшебные квадраты из 16 чисел. Некоторые из них будут обладать основными свойствами.
12 7 6 9
1 14 15 4
8 11 10 5
13 2 3 16

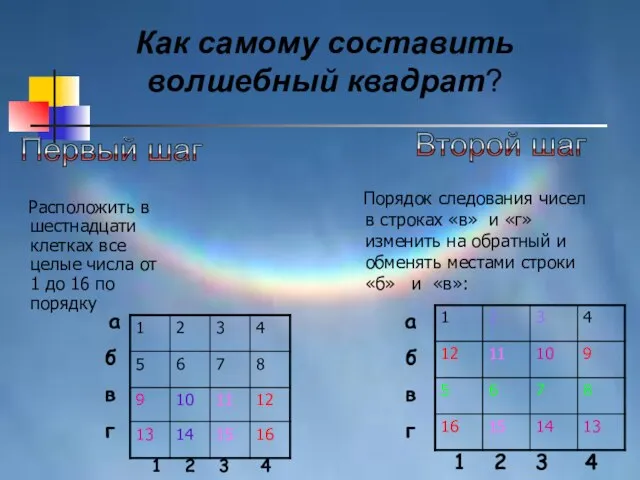
Расположить в шестнадцати клетках все целые числа от 1 до 16 по порядку
Первый шаг
а
б
в
г
1 2 3 4
Как самому составить волшебный квадрат?
Второй шаг
Порядок следования чисел в строках «в» и «г» изменить на обратный и обменять местами строки «б» и «в»:
а
б
в
г
1 2 3 4

Порядок следования чисел во 2 и 3 столбцах изменить на обратный: 1 2 3 4
а
б
в
г
Третий шаг
Четвёртый шаг
Порядок следования чисел в строках «в» и «г» изменить на обратный:
а
б
в
г
1 2 3 4

Волшебный квадрат готов! Можете проверить. Каждая из интересующих нас сумм равна 34 ( это число называется константой волшебного квадрата).

Актуальность ВОЛШЕБНЫХ квадратов в мире, в котором мы живем
-Насколько интересны ВОЛШЕБНЫЕ квадраты в мире, в котором мы живем?
-Я провела небольшое исследование.

Для этого сделала опрос среди учащихся 2 – 6 классов. Участие приняли 60 человек.
Результат представляю в виде круговой диаграммы. ВЫВОД: магические квадраты в среде детей популярны...
66%
16%
18%

Для родителей учеников приготовила экспресс-анкету
1)ваш ребенок увлекается магическими квадратами а)да, б)нет),в)иногда,
2)часто оказываете помощь при выполнении домашнего задания
а)да, б)нет),в)иногда,
3)успеваемость вашего ребенка
а)отличная,
б) хорошая, в)удовлетворительная.

Выясняю интересный факт: при решении задач меньше обращаются за помощью те, кто увлечен магическими квадратами. У этих же ребят и успеваемость лучше по сравнению с теми, кто к квадратам волшебным равнодушен.
Делаю собственный вывод:
В начальных и средних классах очень интересно ребятам решать и составлять магические квадраты. Это помогает в дальнейшем хорошо решать задачи и разбираться в математических упражнениях.

А что ответило взрослое население моего поселка?
Действительно, сейчас идет волна нового увлечения игрой СУДОКУ. В основном потому, что по своей сути - это интереснейшая головоломка.
Постараюсь рассказать о судоку.
Судоку — это головоломка-пазл с числами, ставшая в последнее время очень популярной. В переводе с японского "су" — "цифра", "доку" — "стоящая отдельно". Иногда судоку называют «магическим квадратом». Игровое поле представляет собой квадрат размером 9x9, разделённый на меньшие квадраты со стороной в 3 клетки. Таким образом, всё игровое поле состоит из 81 клетки. В некоторых из них уже в начале игры стоят числа (от 1 до 9). В зависимости от того, сколько клеток уже заполнены, конкретную судоку можно отнести к лёгким или сложным.

Продолжим дальше. В чём ещё актуальность волшебных квадратов в современном мире? Обратимся к Интернету. Выясняем, что существует нумерологический анализатор «Пифагор». В чем его суть?
Это мощная система анализа магического квадрата Пифагора и нумерологической карты, позволяющая проанализировать и понять характер, поведение и мотивацию не только себя, любимого, но и других людей. При помощи анализатора "Пифагор" можно хорошо подготовиться к предстоящей встрече еще до визуального контакта с человеком. Например, после знакомства в сети Интернет, собеседования по телефону и так далее.

В современном мире с помощью нумерологической программы "Пифагор" преподаватели смогут быстрее понять склонности ученика к тому или иному предмету, лучше преподнести материал во время индивидуальных занятий. Психоаналитики смогут быстрее найти проблемные вопросы клиентов. Персоналу отдела кадров программа поможет быстрее разобрать полученные резюме и выделить самых перспективных претендентов.

Продолжая поиски опять-таки в интернете, поражаемся размаху использования магических квадратов. Теперь же они - элементы прогресса нанотехнологии.
Недавно в Интернете появилась интересная информация : фирма "Тошиба" , разрабатывая качественные телевизионные экраны, пришла к выводу, что цветовые ячейки выгодно компоновать по принципу магических квадратов. В этом случае резко повышаются как четкость изображений , так и цветовые переходы. Идеальные магические квадраты имеют в два раза больше цепей ячеек, дающих магическую сумму. Следовательно, и качество изображений экрана телевизора должно еще более улучшиться.

В своей презентации я рассмотрела вопросы, связанные с магическими квадратами. Мне нравилось и нравится составлять волшебные квадраты и думаю, что буду и в дальнейшем совершенствовать свои знания в этом направлении.
Заключение
Удивительная, поистине, магическая красота,
содержащаяся в магических квадратах !

Литература
1) Кордемский Б.А. Математическая смекалка. — ГИФМЛ, 1958. — 576 с.
2) Савин А. П., Я познаю мир.- АСТ, 2004.-475,(5) с.
3)http://www.stereo.ru/whatishat/php?artikle id=254
4) http://narod/ru/disk/2927154000/Магия _чисел_и_слов%20