Восемь способов решения одного тригонометрического уравнения

Восемь способов решения одного
тригонометрического уравнения.
1.Приведение уравнения к однородному.
2.Разложение левой части уравнения на множители.
3.Введение вспомогательного угла.
4.Преобразование разности (или суммы) тригонометрических функций в произведение.
5.Приведение к квадратному уравнению.
6.Возведение обеих частей уравнения в квадрат.
7.Универсальная подстановка.
8.Графическое решение.

Задача. Решите уравнение
различными способами.
sin x – cos x = 1
?

Способ первый. Приведение уравнения к однородному.
Это однородное уравнение первой степени. Делим обе части этого уравнения на
т.к., если
что противоречит тождеству
Получим:
,
.
sin x – cos x = 1

Способ второй. Разложение левой части уравнения на множители.
Далее так, как в первом способе.

Способ третий. Введение вспомогательного угла.
В левой части вынесем - корень квадратный из суммы квадратов коэффициентов при sin х и cos х.
sinα cosβ - cos α sin β = sin (α-β)

Внимание! Эквивалентны ли результаты , полученные
в рассмотренных способах решений данного уравнения sin x – cosx = 1?
Покажем однозначность ответов.
1-й способ
2-й способ

Способ четвертый. Преобразование разности (или суммы) тригонометрических функций в произведение.
Запишем уравнение sin x – cosx = 1 в виде:
Применим формулу разности двух синусов.
Далее так, как в третьем способе.

Способ пятый. Приведение к квадратному уравнению относительно одной функции.
Возведем обе части уравнения в квадрат:
или

Внимание! При решении уравнения обе части уравнения возводились в квадрат, что могло привести к появлению посторонних решений, поэтому необходима проверка.
Сделаем проверку.
Полученные решения эквивалентны объединению трёх решений
Первое и второе решение совпадают с ранее полученными, поэтому не
являются посторонними. Проверять не будем.
Проверим:
Левая часть:
а правая часть уравнения равна 1, следовательно это решение является посторонним.

Способ шестой. Возведение обеих частей уравнения в квадрат. sin x – cos x = 1
Ответ: x = π n, n ∈ Z,
или cos x =0
sin x = 0
x = π n, n ∈ Z

Способ седьмой. Универсальная подстановка .
Выражение всех функций через (универсальная подстановка)
по формулам:
sin x –cosx = 1
Умножим обе части уравнения на

Внимание! Могли потерять корни.Необходима
проверка!
Область допустимых значений первоначального уравнения - всё
множество R . При переходе к tg из рассмотрения выпали значения
x, при которых tg не имеет смысла, т.е.x = π + π n, где n ∈ Z .
Следует проверить , не является ли
x = π +π n, где n ∈ Z решением данного уравнения.
Левая часть sin(π - 2πk) – cos(π + 2πk) = sin π – cos π = 0 – (-1) = 1 и правая часть равна единице. Значит, x = π + π n ,где n ∈ Z является решением данного уравнения.
Ответ: : x= π +π n, n ∈ Z, x= +πn, n ∈ Z.

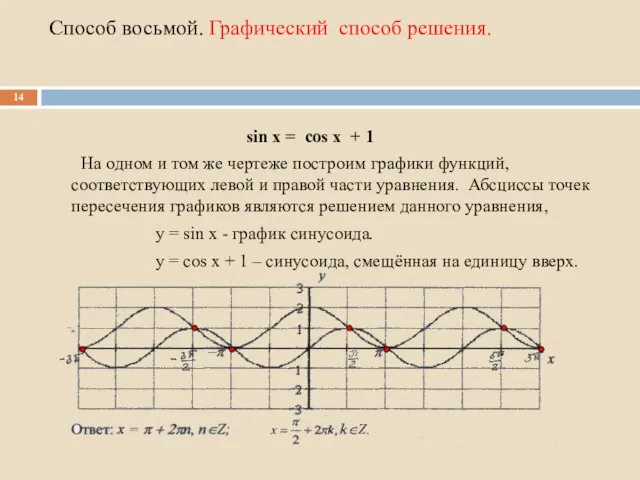
Способ восьмой. Графический способ решения.
На одном и том же чертеже построим графики функций, соответствующих левой и правой части уравнения. Абсциссы точек пересечения графиков являются решением данного уравнения,
у = sin х - график синусоида.
у = соs х + 1 – синусоида, смещённая на единицу вверх.
sin x = cos x + 1

Проверь себя !
Решите самостоятельно, применяя разные способы решения одного и того же тригонометрического уравнения:
sin2x +cos2x = 1

sin 2x + cos2x = 1
sin 2x + cos 2x = 1
2 sin x cos x + cos 2 x – sin2 x = sin 2x + cos 2x,
2 sin x cos x – 2 sin 2 x = 0,
2 sin x ( cos x – sin x ) = 0,
sin x = 0, cos x – sin x = 0,
x = π n, n ∈ Z, tg x = 1,
Ответ: x = π n, n ∈ Z,
Способ: Приведение уравнения к однородному( 1-й способ ).

sin 2x + cos2x = 1
sin 2x + cos 2x = 1,
sin2x – (1 – cos 2x ) = 0,
2 sin x cos x – 2 sin 2x = 0,
Далее так, как первым способом.
Способ: разложение левой части уравнения на множители ( 2 – й способ ).

sin2x + cos2x =1
Способ: преобразование суммы тригонометрических функций в
произведение ( 4-й способ).

sin 2x + cos2x = 1
разделим обе части уравнения на ,
Способ: введение вспомогательного угла (3-й способ).

sin 2x + cos2x = 1
возведём обе части уравнения в квадрат, тогда
Способ: приведение к квадратному уравнению относительно
( 5-й способ).

sin 2x + cos2x = 1
sin 2x + cos2x = 1,
sin 2 2x + 2sin 2x cos2x +cos2x = 1,
2sin 2x cos2x + 1 = 1,
2sin 2x cos2x = 0,
sin 2x = 0, cos2x = 0 ,
2x = π n, n ∈ Z ; 2x = + π n, n ∈ Z,
x = , n ∈ Z ; x = + , n ∈ Z.
Ответ: x= , n ∈ Z; x = + , n ∈ Z.
Способ : возведение обеих частей уравнения в квадрат
( 6 – й способ ).

sin2x + cos2x = 1
Способ: универсальная подстановка (7-й способ).
Ответ:

Оцени себя сам
Реши уравнения: Ответы:
Ключ к ответам: