Содержание
- 2. ЦЕЛЬ РАБОТЫ исследование и изучение основ фрактальной теории, знакомство с математическим обоснованием графической интерпретации фрактальных образов
- 3. ОСНОВНЫЕ НАПРАВЛЕНИЯ РАБОТЫ История появления Определение фрактала Примеры фракталов Классификация фракталов Применение фракталов Заключение Фракталы в
- 4. Фрактал - геометрическая фигура, состоящая из частей, которые могут быть поделены на части, каждая из которых
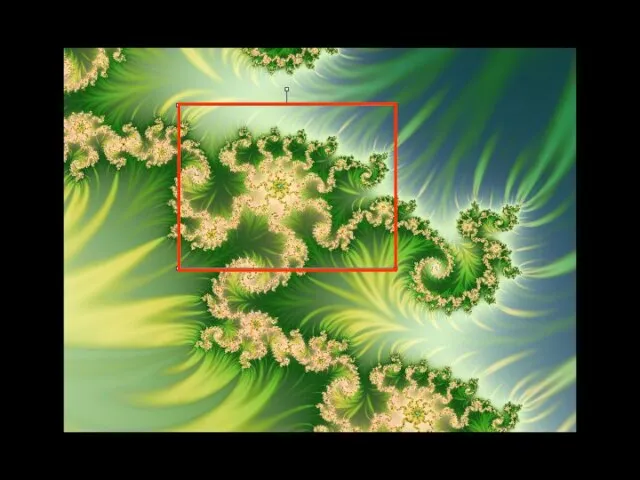
- 8. ФРАКТАЛЫ В ПРИРОДЕ
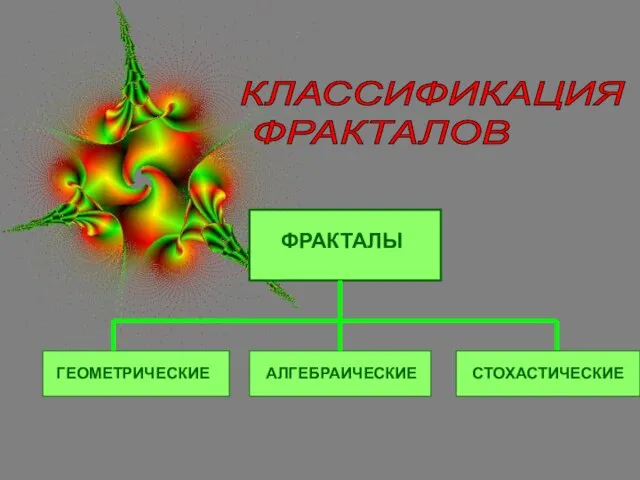
- 9. КЛАССИФИКАЦИЯ ФРАКТАЛОВ ГЕОМЕТРИЧЕСКИЕ
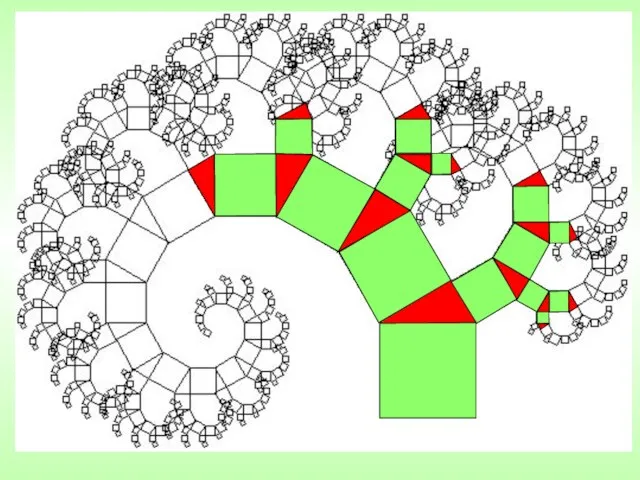
- 10. Это «функции - монстры», которых так называли за недифференцируемость в каждой точке. Геометрические фракталы являются также
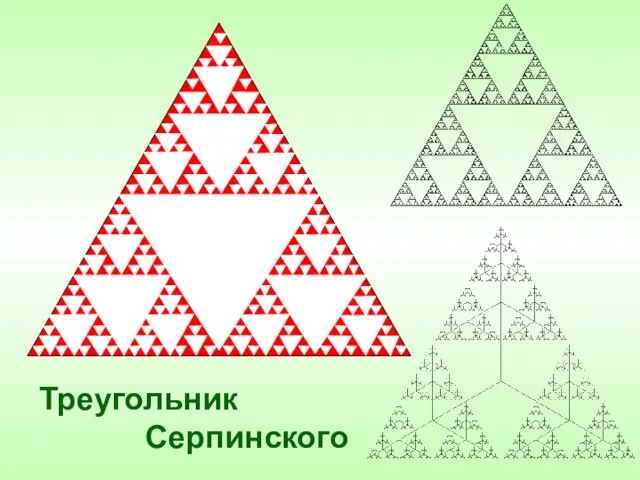
- 11. Треугольник Серпинского
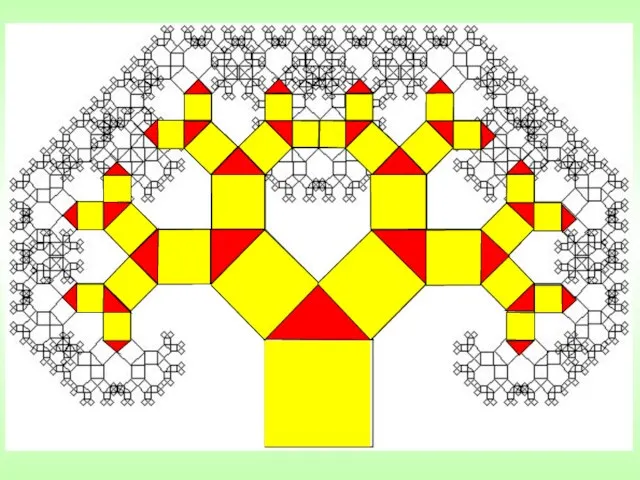
- 12. ковер Серпинского
- 15. Это фракталы, которые можно построить, используя простые алгебраические формулы. Получают их с помощью нелинейных процессов в
- 16. Множество Жюлиа Цвет каждой точки зависит от того, сколько итераций комплексной функции может быть сделано, пока
- 17. МНОЖЕСТВО МАНДЕЛЬБРОТА (окрашено лиловым цветом). Картинка получается с помощью той же процедуры, что и выше. Различие
- 18. Если выбрать показатель степени комплексного числа в виде любого натурального числа n, то получим многочисленный класс
- 20. Это фракталы, при построении которых в итеративной системе случайным образом изменяются какие-либо параметры. Эти фракталы используются
- 23. Скачать презентацию














 Компьютер и здоровье глаз
Компьютер и здоровье глаз Пейзаж.Времена года
Пейзаж.Времена года Организационное и информационное обеспечение фандрейзинга
Организационное и информационное обеспечение фандрейзинга Сложноподчиненное предложение. Повторение и обобщение изученного.
Сложноподчиненное предложение. Повторение и обобщение изученного. История радио и мобильной связи
История радио и мобильной связи А как ты знаешь физику?
А как ты знаешь физику? Презентация на тему Нефтяная промышленность
Презентация на тему Нефтяная промышленность  Изобразительное искусство барокко
Изобразительное искусство барокко Как начать бизнес в интернете?
Как начать бизнес в интернете? Sony Ericsson: Из VGA в HD
Sony Ericsson: Из VGA в HD Символика Краснодарского края
Символика Краснодарского края Для умных женщин Одна супружеская пара поехала в выходные на озеро порыбачить.
Для умных женщин Одна супружеская пара поехала в выходные на озеро порыбачить. Бюджет для граждан по Решению Совета депутатов МО Александровский район от 23.12.2020
Бюджет для граждан по Решению Совета депутатов МО Александровский район от 23.12.2020 Children's behavior and its influence on their future acts
Children's behavior and its influence on their future acts РАНХиГС_очно_27.09.2022_Акцнт, реф, защ, техн ОС
РАНХиГС_очно_27.09.2022_Акцнт, реф, защ, техн ОС Слова-паразиты, или экология речи
Слова-паразиты, или экология речи Иммунная система и канцерогенез
Иммунная система и канцерогенез  Подарки AI Journey. Предложения. Сберклауд
Подарки AI Journey. Предложения. Сберклауд Философские теории неврозов
Философские теории неврозов Реализация и изучение игры «Жизнь» в среде электронных таблиц (MS Ecxel)
Реализация и изучение игры «Жизнь» в среде электронных таблиц (MS Ecxel) Деструктивность учащегося и образовательной среды: точки соприкосновения
Деструктивность учащегося и образовательной среды: точки соприкосновения БАЛАНС-2W: ПОДГОТОВКА СПРАВКИ 2-НДФЛ
БАЛАНС-2W: ПОДГОТОВКА СПРАВКИ 2-НДФЛ Подготовка граждан к военной службе
Подготовка граждан к военной службе Ультразвуковые накладные расходомеры Flexim
Ультразвуковые накладные расходомеры Flexim Презентация для заказных проектов
Презентация для заказных проектов Поступление на государственную службу
Поступление на государственную службу Оценка достижений учащихся в разновозрастной группе
Оценка достижений учащихся в разновозрастной группе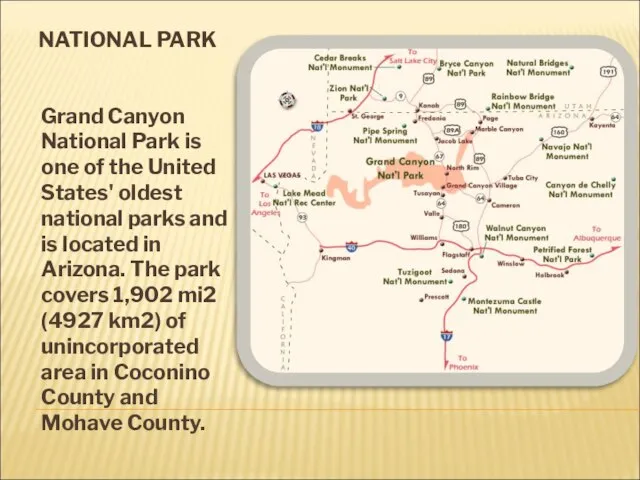 Grand Canyon National Park
Grand Canyon National Park