Содержание
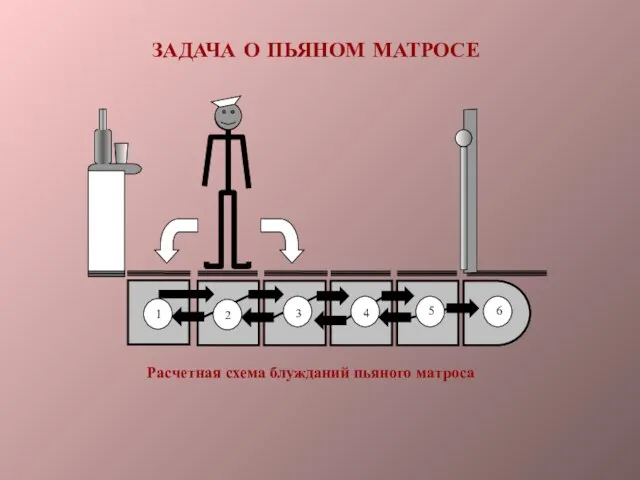
- 2. ЗАДАЧА О ПЬЯНОМ МАТРОСЕ
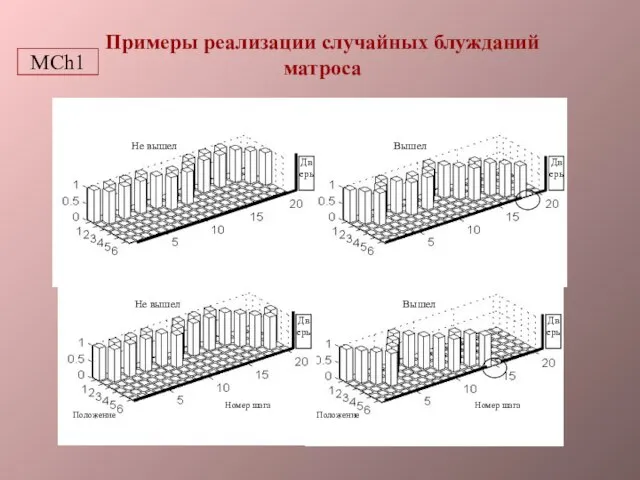
- 3. Примеры реализации случайных блужданий матроса MCh1
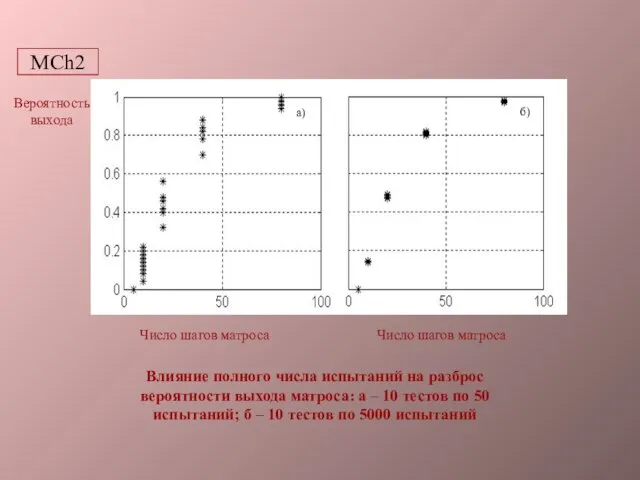
- 4. Вероятность выхода Число шагов матроса Число шагов матроса Влияние полного числа испытаний на разброс вероятности выхода
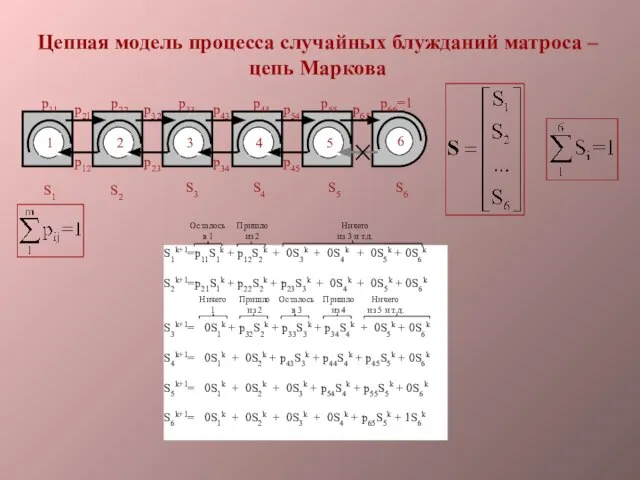
- 5. Цепная модель процесса случайных блужданий матроса – цепь Маркова
- 6. Sk+1=PSk Матричная запись qk=S5kp65=S6k+1 - S6k
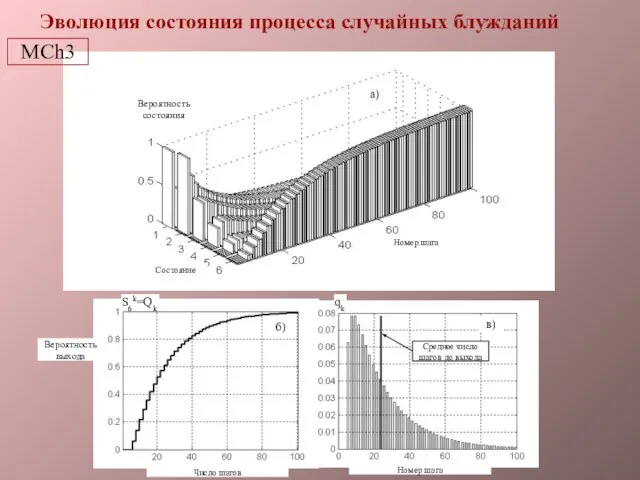
- 7. Эволюция состояния процесса случайных блужданий MCh3
- 8. Одномерная диффузия. Виды и влияние краевых условий d p12=d p32=d+v p22=1-2d-v v Выделение симметричной составляющей вероятностей
- 9. Эволюция содержания диффундирующего вещества на отрезке с закрытыми границами S∞=РS∞ → S∞ - один из собственных
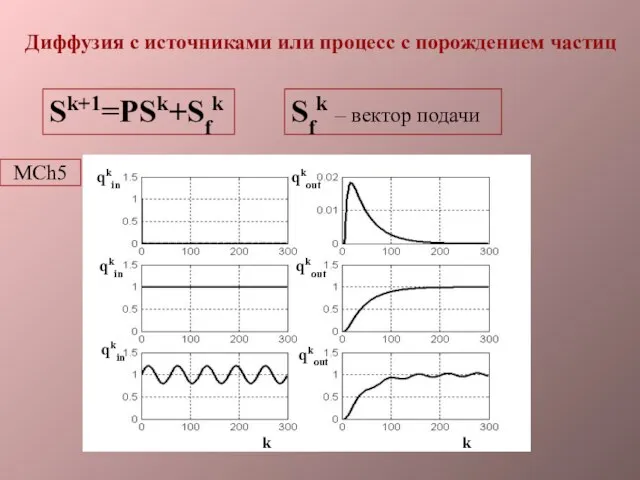
- 10. Диффузия с источниками или процесс с порождением частиц Sk+1=PSk+Sfk Sfk – вектор подачи MCh5
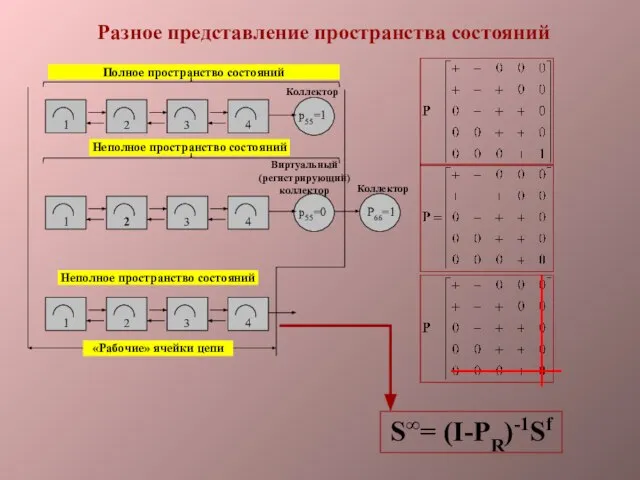
- 11. Коллектор p55=1 Виртуальный (регистрирующий) коллектор p55=0 P66=1 Коллектор «Рабочие» ячейки цепи Полное пространство состояний Неполное пространство
- 12. Случайные блуждания и диффузия на плоскости 5 тестов по 1000 испытаний Число шагов матроса Вероятность выхода
- 13. Структура переходной матрицы
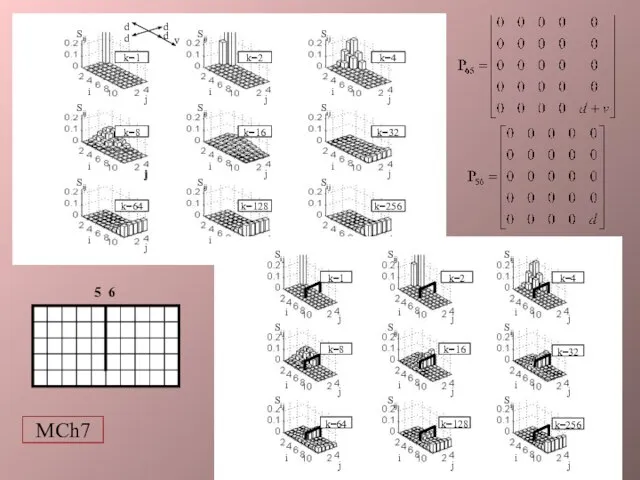
- 14. 5 6 MCh7
- 15. Конец лекции 1 Спасибо за внимание
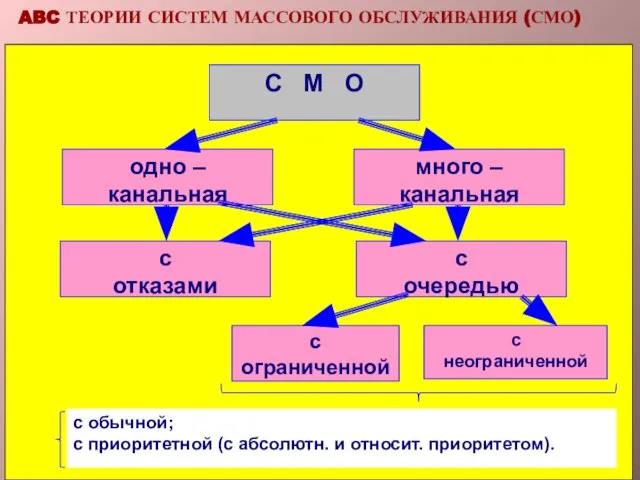
- 16. ABC ТЕОРИИ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ (СМО)
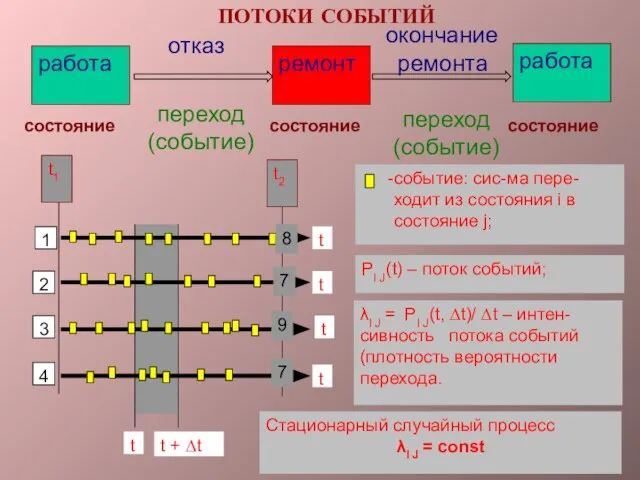
- 17. событие: сис-ма пере- ходит из состояния i в состояние j; PI J(t) – поток событий; λI
- 18. N систем: NS1 - работает, NS2 - не работает (в ремонте) уходит из 1 : NS1ν
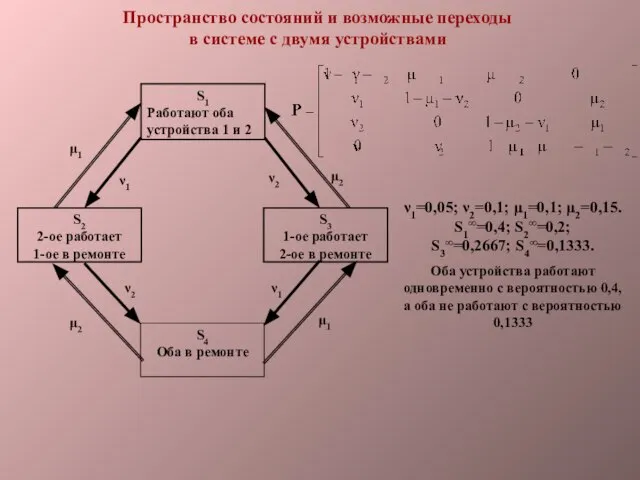
- 19. S1 Работают оба устройства 1 и 2 S2 2-ое работает 1-ое в ремонте S3 1-ое работает
- 20. Многоканальная СМО с отказами Потому что все равно, какой канал освободится, а их 2 ν -
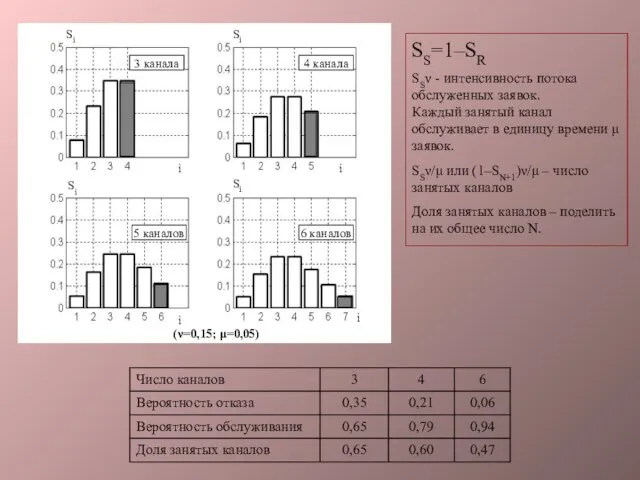
- 21. SS=1–SR SSν - интенсивность потока обслуженных заявок. Каждый занятый канал обслуживает в единицу времени μ заявок.
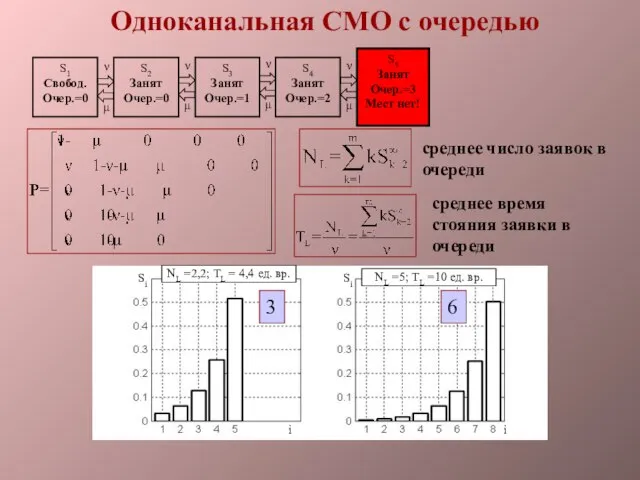
- 22. Одноканальная СМО с очередью среднее число заявок в очереди среднее время стояния заявки в очереди NL
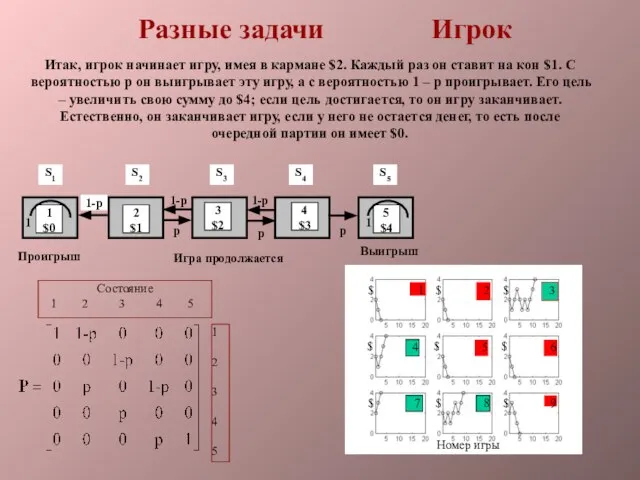
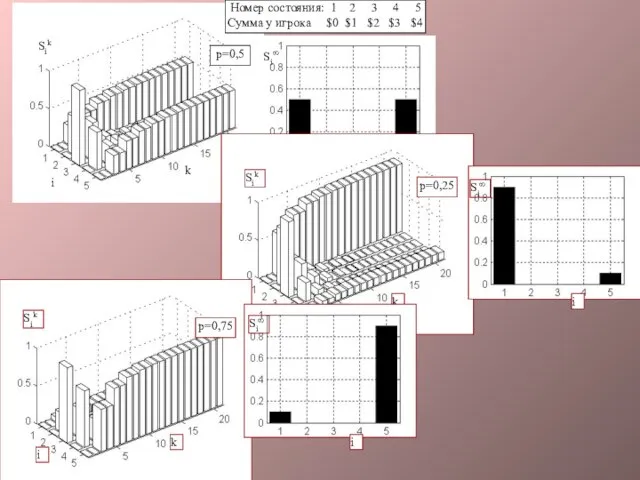
- 23. Итак, игрок начинает игру, имея в кармане $2. Каждый раз он ставит на кон $1. С
- 25. Разные задачи Пенсионные отчисления Неработающие дети (1), работающие взрослые (2), пенсионеры (3) и умершие (4). Пусть
- 27. Скачать презентацию









 Авторы: Семёнова Софья Петрова Елена 8 класс МОУ Бондарская СОШ 2010 Конкурс «Мой учитель»
Авторы: Семёнова Софья Петрова Елена 8 класс МОУ Бондарская СОШ 2010 Конкурс «Мой учитель» В гостях у сказки, устройство детской разновозрастной площадки
В гостях у сказки, устройство детской разновозрастной площадки Зелёная жаба
Зелёная жаба Правосознание и правовая культура
Правосознание и правовая культура НЕ и НИ. Слитное и раздельное написание
НЕ и НИ. Слитное и раздельное написание Отклоняющееся и противоправное поведение
Отклоняющееся и противоправное поведение Техника безопасности на уроках информатики
Техника безопасности на уроках информатики Нарушения слуха
Нарушения слуха Цилиндр
Цилиндр Фирма в условиях совершенной конкуренции
Фирма в условиях совершенной конкуренции Для умных женщин Одна супружеская пара поехала в выходные на озеро порыбачить.
Для умных женщин Одна супружеская пара поехала в выходные на озеро порыбачить. Пример схемы для ЕАСД. Схемы размещения моторовагонных депо
Пример схемы для ЕАСД. Схемы размещения моторовагонных депо Казахстанский опыт борьбы с коррупцией
Казахстанский опыт борьбы с коррупцией Совещание с представителями органов исполнительной власти субъектов Российской Федерации, осуществляющих управление
Совещание с представителями органов исполнительной власти субъектов Российской Федерации, осуществляющих управление Часть 2.
Часть 2. Тема урока:
Тема урока: Обеспечение успешной адаптации ребенка к обучению в школе
Обеспечение успешной адаптации ребенка к обучению в школе Презентация на тему Геометрические тела и плоские фигуры (6-9 класс)
Презентация на тему Геометрические тела и плоские фигуры (6-9 класс) День победы
День победы Африка
Африка Россия - мать, жена, сестра, невеста!
Россия - мать, жена, сестра, невеста! Наука. Технологии. Я
Наука. Технологии. Я Искусство
Искусство Стратегия формирования привлекательности товарного предложения
Стратегия формирования привлекательности товарного предложения Родительское собрание
Родительское собрание К ВОПРОСУ О ЗЕРНОВОМ СОСТАВЕ МЕЛКОГО ЗАПОЛНИТЕЛЯ ДЛЯ БЕТОНОВ Козлов А.В., канд. техн. наук, ОАО ЦНИИС
К ВОПРОСУ О ЗЕРНОВОМ СОСТАВЕ МЕЛКОГО ЗАПОЛНИТЕЛЯ ДЛЯ БЕТОНОВ Козлов А.В., канд. техн. наук, ОАО ЦНИИС Управление предприятием и его устойчивость. Лекция 2
Управление предприятием и его устойчивость. Лекция 2 Человек – личность
Человек – личность