Содержание
- 2. Задачи на чередование 1.На плоскости располо- жено 11 шестеренок,со- единенных по цепочке. Могут ли все шестеренки
- 3. Задачи на чередование 2.Может ли шахматный конь выйти с левого ниж- него углового поля,обойти всю доску
- 4. Разбиение на пары 1.Все костяшки домино выложили в цепь.На од- ном конце оказалось 5 оч- ков.Сколько
- 5. Четность и нечетность 1.Кузнечик прыгал вдоль прямой и вернулся в ис- ходную точку(длина прыж ка 1
- 6. Четность и нечетность 2 Всегда ли можно рас- ставить по росту 1997 че- ловек,если разрешается переставлять
- 8. Скачать презентацию





 Sociological Research Methods and Techniques
Sociological Research Methods and Techniques  Презентация на тему Лесные и торфяные пожары
Презентация на тему Лесные и торфяные пожары  Уфимцева Александра Семёновна
Уфимцева Александра Семёновна Похвальное слово знакам препинания
Похвальное слово знакам препинания Методы изучения и оценки психических состояний человека
Методы изучения и оценки психических состояний человека Профессиональные программы
Профессиональные программы Образование сложных слов
Образование сложных слов Синус, косинус, тангенс острого угла прямоугольного треугольника
Синус, косинус, тангенс острого угла прямоугольного треугольника Живи, родник
Живи, родник Математический
Математический Интерактивная модульная дорожка
Интерактивная модульная дорожка Компания “ГРАФ-ПАРКЕТ” рада представить Вашему вниманию образцы нашей продукции.
Компания “ГРАФ-ПАРКЕТ” рада представить Вашему вниманию образцы нашей продукции. Промышленные способы обработки продуктов
Промышленные способы обработки продуктов Презентация на тему Микены и Троя
Презентация на тему Микены и Троя  Сортовой прокат
Сортовой прокат Презентация на тему Третьеиюньский переворот
Презентация на тему Третьеиюньский переворот Глаза, нос и губы Рисуем части лица. Готовимся рисовать портрет. Часть 2
Глаза, нос и губы Рисуем части лица. Готовимся рисовать портрет. Часть 2 Due dilligence
Due dilligence Строение и функции мышц
Строение и функции мышц «Секрет успеха в том, чтобы использовать как можно лучше то, что тебе дано»Джо Райан
«Секрет успеха в том, чтобы использовать как можно лучше то, что тебе дано»Джо Райан Муниципальной ресурсный центр «Система здоровьесберегающей деятельности в ОУ»
Муниципальной ресурсный центр «Система здоровьесберегающей деятельности в ОУ» Презентация 6 класса МОУ «Кармамейская ООШ» Канашского района ЧР
Презентация 6 класса МОУ «Кармамейская ООШ» Канашского района ЧР Профессиональная готовность будущих педагогов к работе в интегрированных учебных заведениях
Профессиональная готовность будущих педагогов к работе в интегрированных учебных заведениях Том Диксон
Том Диксон Презентация на тему Арифметические действия 4 класс
Презентация на тему Арифметические действия 4 класс  Subkulturе Hippie
Subkulturе Hippie Экология в политике XXI века
Экология в политике XXI века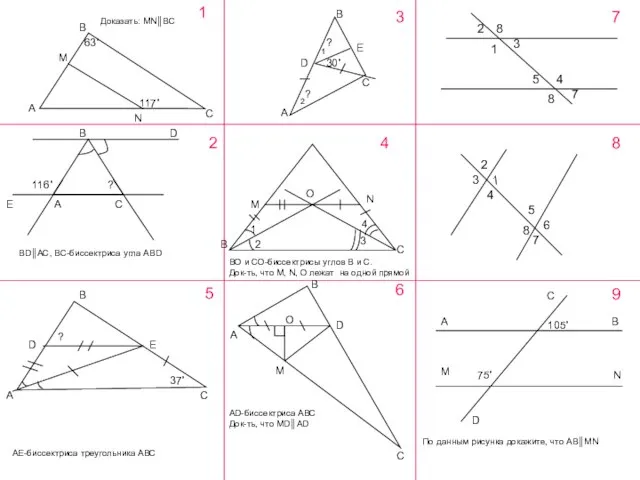 А М В С N 1 2 3 4 BD EАC A B E C D O M N B C B CA DE 5 A B D M O C 6 2 8 1 3 4 5 7 8 1 3 4 2 5 8 6 7 117˚ 63˚ 30˚ ? ? Доказать: MNBC BDAC, BC-биссектриса.
А М В С N 1 2 3 4 BD EАC A B E C D O M N B C B CA DE 5 A B D M O C 6 2 8 1 3 4 5 7 8 1 3 4 2 5 8 6 7 117˚ 63˚ 30˚ ? ? Доказать: MNBC BDAC, BC-биссектриса.