Вычислительная геометрия

Векторное произведение векторов

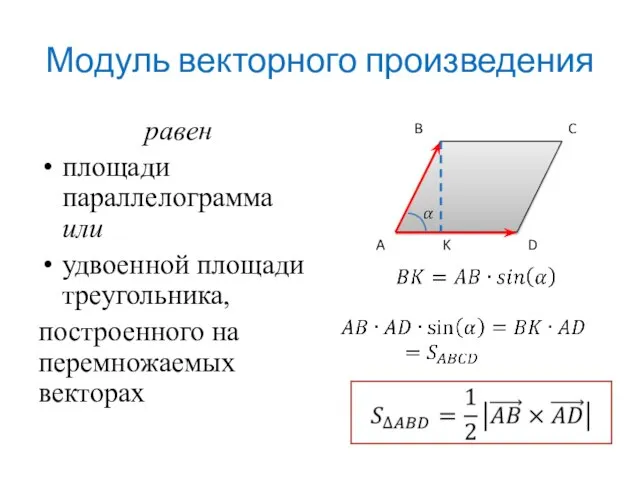
Модуль векторного произведения
равен
площади параллелограмма или
удвоенной площади треугольника,
построенного на перемножаемых векторах

Проекция векторного произведения
Ось z направлена к нам

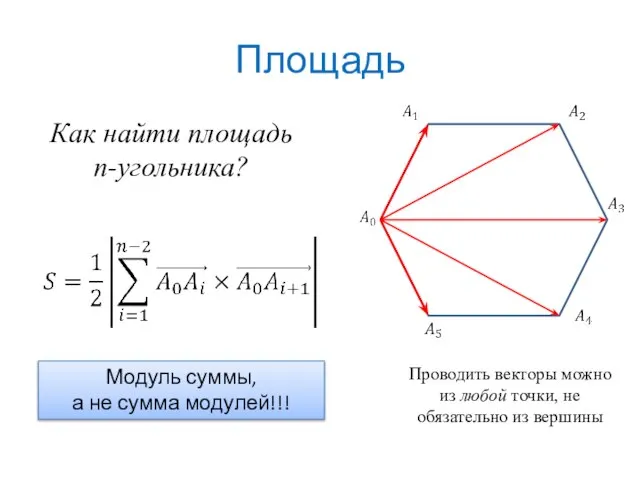
Площадь
Как найти площадь
n-угольника?
Модуль суммы,
а не сумма модулей!!!
Проводить векторы можно из любой точки, не обязательно из вершины

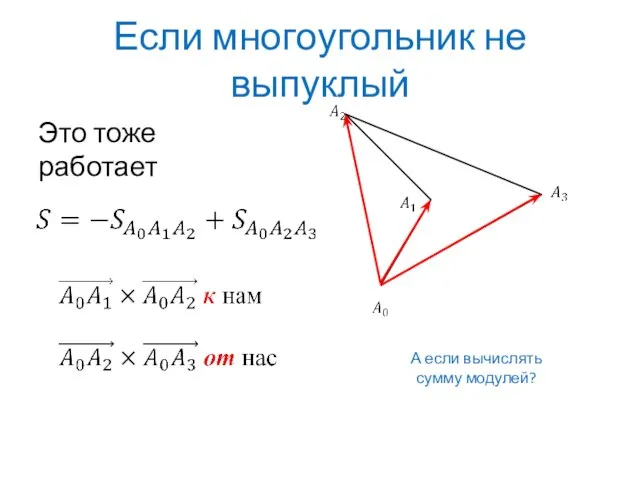
Если многоугольник не выпуклый
Это тоже работает
А если вычислять
сумму модулей?

Точка и прямая
Даны координаты точек A, B, C.
Как расположена точка C относительно прямой AB:
выше прямой;
ниже прямой;
на прямой?
B
A
. C
Вектор направлен
к нам – точка выше прямой
от нас – точка ниже прямой
равен нулю – точка на прямой

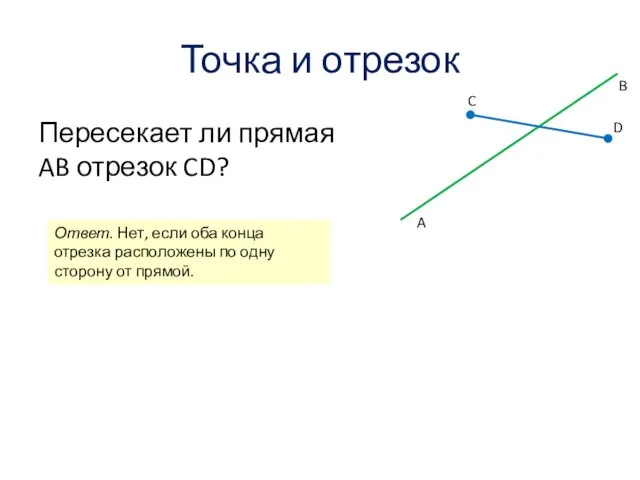
Точка и отрезок
Пересекает ли прямая AB отрезок CD?
A
B
C
D
Ответ. Нет, если оба конца отрезка расположены по одну сторону от прямой.

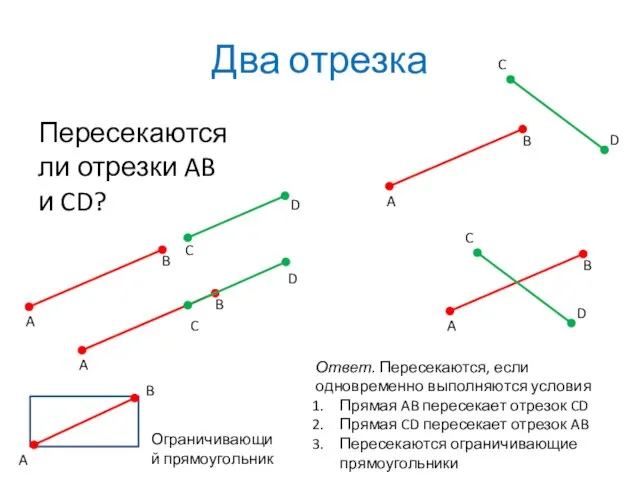
Два отрезка
Пересекаются ли отрезки AB и CD?
Ответ. Пересекаются, если одновременно выполняются условия
Прямая AB пересекает отрезок CD
Прямая CD пересекает отрезок AB
Пересекаются ограничивающие прямоугольники
A
B

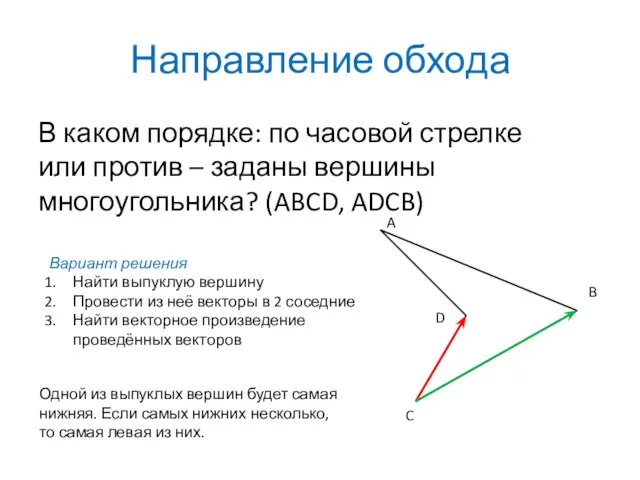
Направление обхода
В каком порядке: по часовой стрелке или против – заданы вершины многоугольника? (ABCD, ADCB)
Вариант решения
Найти выпуклую вершину
Провести из неё векторы в 2 соседние
Найти векторное произведение проведённых векторов
Одной из выпуклых вершин будет самая нижняя. Если самых нижних несколько, то самая левая из них.
A
B
C
D