Содержание
- 2. Analiza współzależności Współczynnik korelacji liniowej Pearsona Współczynnik korelacji rang Spearmana Analiza zależności Liniowa funkcja regresji Badanie
- 3. ISTOTA KORELACJI I REGRESJI KORELACJA daje możliwość stwierdzenia, czy istnieje związek (niekoniecznie przyczynowo-skutkowy) miedzy badanymi cechami
- 4. Sir Francis Galton – 1822-1911, prekursor badań nad inteligencją, statystyk, meteorolog, antropolog, kryminolog. Pisarz, lekarz. W
- 5. Zależność przyczynowa – rodzaj zależności, w której jesteśmy w stanie wskazać, która ze zmiennych stanowi przyczynę
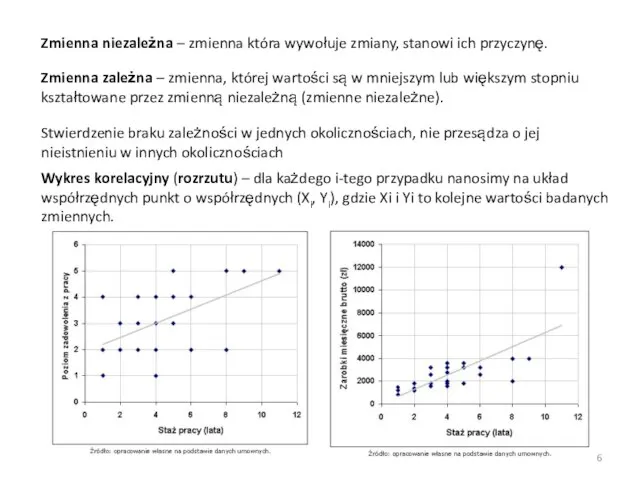
- 6. Zmienna niezależna – zmienna która wywołuje zmiany, stanowi ich przyczynę. Zmienna zależna – zmienna, której wartości
- 7. WSPÓŁCZYNNIK KORELACJI PEARSONA
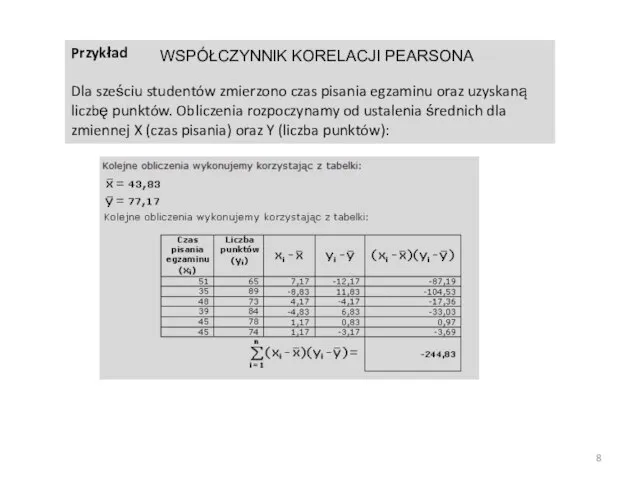
- 8. Przykład Dla sześciu studentów zmierzono czas pisania egzaminu oraz uzyskaną liczbę punktów. Obliczenia rozpoczynamy od ustalenia
- 9. WSPÓŁCZYNNIK KORELACJI PEARSONA
- 10. WSPÓŁCZYNNIK KORELACJI PEARSONA
- 11. WSPÓŁCZYNNIK KORELACJI PEARSONA
- 12. WSPÓŁCZYNNIK KORELACJI PEARSONA
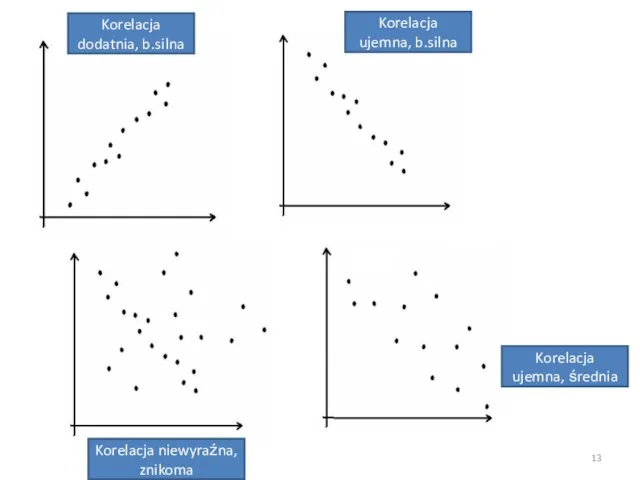
- 13. Korelacja ujemna, średnia Korelacja niewyraźna, znikoma Korelacja ujemna, b.silna Korelacja dodatnia, b.silna
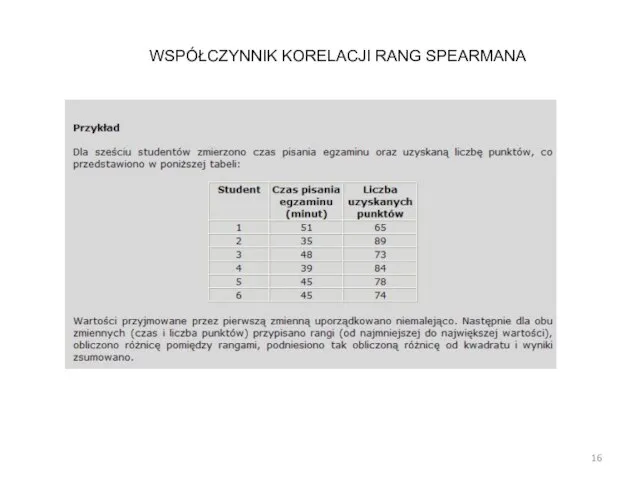
- 14. Współczynnik korelacji rang Spearmana służy do opisu siły korelacji dwóch cech w przypadku gdy: Cechy są
- 15. WSPÓŁCZYNNIK KORELACJI RANG SPEARMANA
- 16. WSPÓŁCZYNNIK KORELACJI RANG SPEARMANA
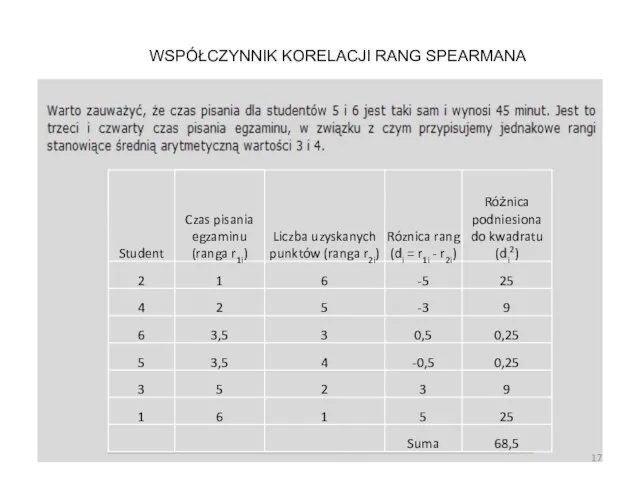
- 17. WSPÓŁCZYNNIK KORELACJI RANG SPEARMANA
- 18. WSPÓŁCZYNNIK KORELACJI RANG SPEARMANA
- 19. W modelach regresji zależność pomiędzy jedną lub większą ilością zmiennych niezależnych (predykatory, zmienne wyjaśniające) a zmienną
- 20. Karol Fryderyk Gauss, ur. w 1777 roku w Niemczech. Ojciec Karola był pomocnikiem murarskim i swojego
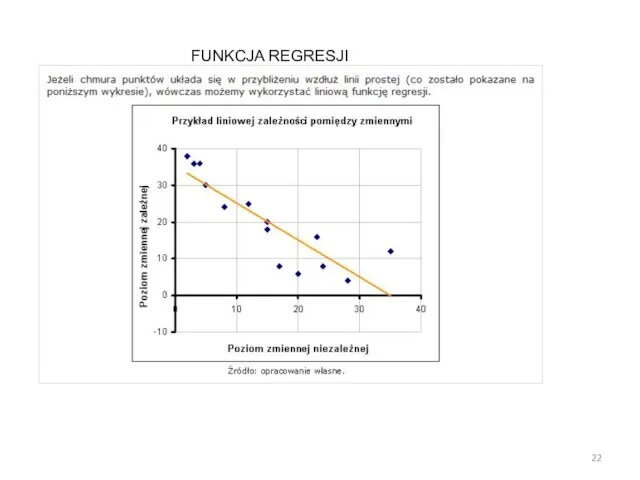
- 21. Funkcja regresji - to narzędzie do badania powiązań między zmiennymi. Funkcja regresji to analityczny wyraz przyporządkowania
- 22. FUNKCJA REGRESJI
- 23. FUNKCJA REGRESJI
- 24. Mamy do czynienia tylko z jedną zmienną niezależną X. Zależność pomiędzy zmienną niezależną X a zmienną
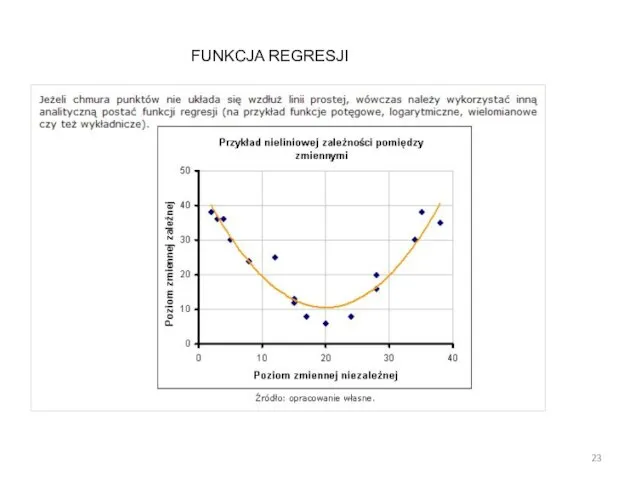
- 25. FUNKCJA REGRESJI
- 26. FUNKCJA REGRESJI
- 27. W wyjaśnianiu wielu zjawisk istotną rolę odgrywają zmienne niemierzalne, tj. jakościowe. I tak, na wielkość popytu
- 28. Dla danych jakościowych, mierzonych na skali nominalnej lub porządkowej analizę współzależności zwykle rozpoczynamy od utworzenia tabeli
- 30. Скачать презентацию




















 Откуда берётся и куда девается мусор
Откуда берётся и куда девается мусор Иллюстрации к повести Куприна «Гранатовый браслет». Кадры из фильма.
Иллюстрации к повести Куприна «Гранатовый браслет». Кадры из фильма. Духовная жизнь страны
Духовная жизнь страны Защити себя сама
Защити себя сама Начальная школа XXI века «Окружающий мир» авт. Н.Ф. Виноградова 1 класс.
Начальная школа XXI века «Окружающий мир» авт. Н.Ф. Виноградова 1 класс. Научно-технические журналы строительного комплекса – славная история,трудное настоящее,неопределенное будущее
Научно-технические журналы строительного комплекса – славная история,трудное настоящее,неопределенное будущее Зарубежная литература эпохи Просвещения
Зарубежная литература эпохи Просвещения Обращение в Европейский суд по правам человека: критерии приемлемости жалобы, правила обращения
Обращение в Европейский суд по правам человека: критерии приемлемости жалобы, правила обращения Школьная площадка МБОУ Марининской СОШ № 16
Школьная площадка МБОУ Марининской СОШ № 16 Моральные требования, предъявляемые к юридической профессии
Моральные требования, предъявляемые к юридической профессии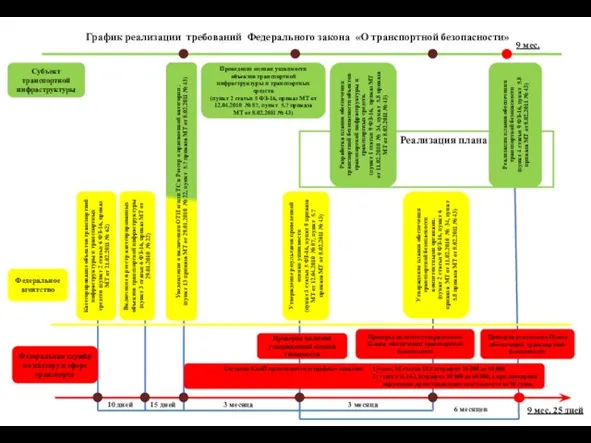 Реализация плана
Реализация плана Аттестация педагогических работников государственных и муниципальных образовательных учреждений Санкт-Петербург
Аттестация педагогических работников государственных и муниципальных образовательных учреждений Санкт-Петербург Виды дорожно-транспортных проишевствий
Виды дорожно-транспортных проишевствий Преимущества МС для ИС
Преимущества МС для ИС Операции по управлению персоналом
Операции по управлению персоналом Презентация на тему А.С. Пушкин
Презентация на тему А.С. Пушкин  История развития туризма и гостеприимства
История развития туризма и гостеприимства Развитие инновационной экономики. Инвестирование в высокотехнологичные проекты на раннем этапе развития
Развитие инновационной экономики. Инвестирование в высокотехнологичные проекты на раннем этапе развития Растениеводство
Растениеводство Укрепление системы органов внутренних дел во второй половине 1960-х - 1980-е гг
Укрепление системы органов внутренних дел во второй половине 1960-х - 1980-е гг Урок литературного чтения
Урок литературного чтения Творческий путь Федора Ивановича Тютчева
Творческий путь Федора Ивановича Тютчева Стихи и загадки про цифры
Стихи и загадки про цифры Турбулентные газопромыватели. (Лекция 13)
Турбулентные газопромыватели. (Лекция 13) Электронной Библиотеке - Электронный Абонемент
Электронной Библиотеке - Электронный Абонемент Словари
Словари Василий Васильевич Кандинский (16 декабря 1866 -13 декабря 1944 )
Василий Васильевич Кандинский (16 декабря 1866 -13 декабря 1944 ) Избавляемся от статического электричества
Избавляемся от статического электричества