XVII Межрегиональная олимпиада по математике и криптографии

Задача №1
Сообщение на русском языке состоит из 6 строк. В каждой строке кроме последней ровно 18 букв (буквы в строках стоят точно друг под другом). Для зашифрования сообщения каждую его букву заменили парой цифр в соответствии с ее порядковым номером в алфавите (А – на 01, Б – на 02, …, Я –на 33). В результате получилась таблица цифр, в которой 36 столбцов. Затем эту таблицу разделили на вертикальные полосы: по три столбца в каждой. После чего полосы переставили в неизвестном порядке

Задача №1 (продолжение)
Получили вот что:
316 001 190 014 013 150 171 240 120 131 105 614
010 810 050 610 012 161 121 200 614 120 401 117
619 501 172 327 171 041 061 221 010 033 801 016
115 313 192 312 030 130 160 103 210 013 620 016
512 060 061 250 061 825 16 103 310
Какой текст был зашифрован?

Задача №1(решение)
316 001 190 014 013 150 171 240 120 131 105 614
010 810 050 610 012 161 121 200 614 120 401 117
619 501 172 327 171 041 061 221 010 033 801 016
115 313 192 312 030 130 160 103 210 013 620 016
512 060 061 250 061 825 16 103 310
На четных местах – 1,2,4,9,11,12 столбцы; на нечетных – 3,5,6,7,8,10 столбцы.
С учетом числа строк в каждом столбце, получаем что последними были 10,2,7,4 или 10,4,7,2. Подходит только второй вариант.

Задача №1(решение)
Преобразуя пары цифр в буквы, получим:
ЛИМПИА
КЕИКРИ
ВЯЩЕНА
АЯКОВЛ
О

Задача №1(решение)
Подбирая по принципу «читаемости» фрагментов слов, восстанавливаем расположение остальных столбцов.
Ответ: Семнадцатая олимпиада по математике и криптографии посвящена столетию Ивана Яковлевича Верченко.

Задача №2
Пусть Cn(a,b) = abab…ab – целое число, десятичная запись которого образована n–кратным повторением пары цифр a и b, где a≠0.
Выясните, при каких n число Cn(a,b) делится на 21 при любых значениях a и b.

Задача №2 (решение)
abab…ab = ab ⋅ 0101…01
a, b – любые, поэтому n должно быть таким, что 0101..01 делится на 21
0101..01 делится на 3⬄ n делится на 3
Делимость на 7 обеспечена, т.к. 010101=7⋅1443
Ответ: n=3k, k∈N.

Задача №3
Сообщение зашифровано следующим образом. Над буквами сообщения надписывается числовая после-довательность, образованная периоди-ческим повторением шести цифр, образующих дату. Например, шестерка 181107 отвечает дате 18 ноября 2007 года. После этого буквы сообщения заменяются буквой алфавита, циклически отстоящей от нее справа на число букв, указанное цифрой над ней.

Задача №3 (пример)
ОЛИМПИАДА…
181107181…
ПТЙНППБЛБ…

Задача №3 (продолжение)
Можно ли прочитать зашифрованное таким образом сообщение
Т П И Ё Р Ж Е М А А С Ф С Г Ь О Г Х Ж П Н,
если неизвестна дата его написания?

Задача №3 (решение)
В дате первая цифра – 0,1,2 или 3
Третья – 0 или 1
Выпишем возможные буквы

Задача №3(решение)
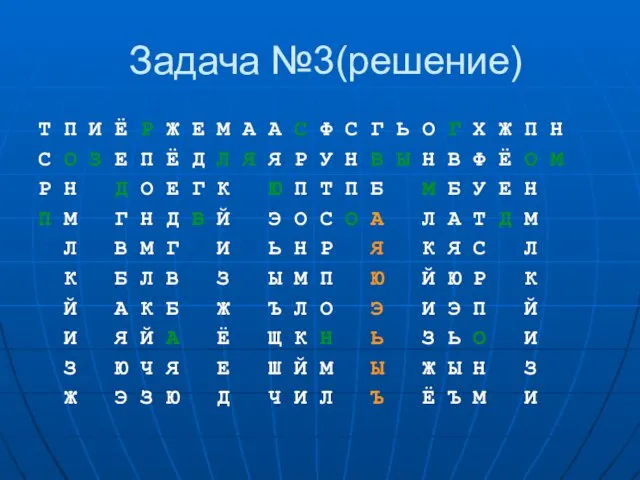
Т П И Ё Р Ж Е М А А С Ф С Г Ь О Г Х Ж П Н
С О З Е П Ё Д Л Я Я Р У Н В Ы Н В Ф Ё О М
Р Н Д О Е Г К Ю П Т П Б М Б У Е Н
П М Г Н Д В Й Э О С О А Л А Т Д М
Л В М Г И Ь Н Р Я К Я С Л
К Б Л В З Ы М П Ю Й Ю Р К
Й А К Б Ж Ъ Л О Э И Э П Й
И Я Й А Ё Щ К Н Ь З Ь О И
З Ю Ч Я Е Ш Й М Ы Ж Ы Н З
Ж Э З Ю Д Ч И Л Ъ Ё Ъ М И

Задача №4
Сообщение на русском языке, состоящем из 63 букв и восклицательного знака, зашифровано с использованием так называемой «поворотной решетки», которая представляет собой трафарет, изготовленный из квадратного листа клетчатой бумаги 8 на 8. В трафарете вырезаны 16 клеток. Одна сторона трафарета помечена. При наложении трафарета на чистый лист бумаги четырьмя возможными способами (помеченной стороной вверх, вправо, вниз, влево) его вырезы полностью покрывают всю площадь квадрата, причем каждая клетка оказывается под вырезом ровно один раз.

Задача №4 (продолжение)
Буквы сообщения построчно сверху вниз и слева направо вписываются в вырезы трафарета (пробелы между словами игнорируются). После заполнения всех вырезов буквами сообщения трафарет располагается в следующем положении и т.д. Результат зашифрования сообщения представлен на рисунке. Найдите исходное сообщение

Задача №4 (продолжение)

Задача №4 (решение)

Задача №4 (ответ)
смещениетрафарет
авшифреповоротна
ярешеткапозволяе
тпрочитатьтекст!
Смещение трафарета в шифре поворотная решетка позволяет прочитать текст!

Задача №5
В здании находится восемь серверов. Они расположены в вершинах куба. Эти серверы объединены в сеть, причем два сервера соединены линией связи "напрямую" в том и только том случае, когда они соответствуют двум соседним вершинам куба. Кроме того, два из этих серверов соединены дополнительно по радиоканалу.

Задача №5 (продолжение)
Какое наименьшее число основных линий связи придется вывести из строя злоумышленнику, для того что бы потерялась связность сети (т.е. станет невозможно доставить информацию с одного из серверов на другой, даже через серверы-посредники)

Задача №5 (решение)
Удаление ребер должно «разбить» сеть на три компоненты.
Удалив 5 ребер, это легко сделать.
Обоснование, что 4 ребрами обойтись нельзя проводится перебором по минимальному числу вершин в компоненте. Оно равно 1 или 2.

Задача №6
Разложить на простые множители число 320+34+1, если известно, что оно делится на 167.

Задача №6 (решение)
x=34
x5+x+1= x5+x+1+x4-x4+x3-x3+x2-x2 =
=x5 +x4+x3+x2 +x+1-x4-x3-x2=
=x3(x2+x+1)+x2+x+1-x2(x2+x+1)=
=(x2+x+1)(x3-x2 +1)
x2+x+1=38+34+1 = 38+2⋅34+1-34 =
=(34+1)2-34=91⋅73=7⋅13⋅73

Задача №6 (решение)
x3-x2 +1=x(x2+x+1)+x+3
x+3=84=7⋅12
x2+x+1 на 7 делится
x3-x2 +1=x⋅7⋅13⋅73+7⋅12=
=7⋅(34⋅13 ⋅73+12)=7⋅167⋅449.
Ответ: 72⋅13⋅73⋅167⋅449.