Языки программирования и методы трансляции

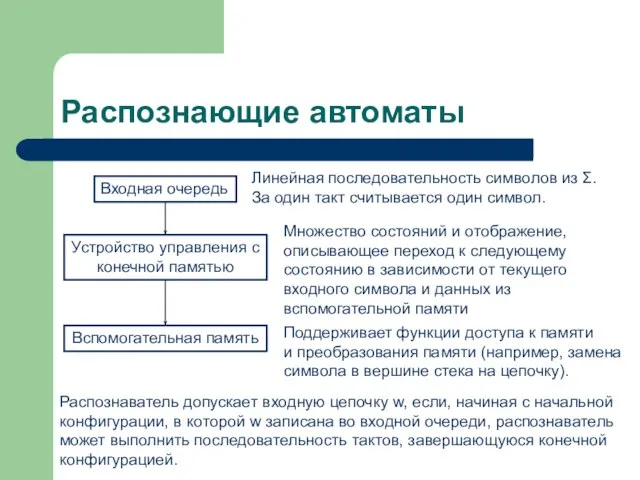
Распознающие автоматы
Входная очередь
Устройство управления с конечной памятью
Вспомогательная память
Линейная последовательность символов из Σ.
За один такт считывается один символ.
Поддерживает функции доступа к памяти
и преобразования памяти (например, замена символа в вершине стека на цепочку).
Множество состояний и отображение, описывающее переход к следующему состоянию в зависимости от текущего входного символа и данных из вспомогательной памяти
Распознаватель допускает входную цепочку w, если, начиная с начальной конфигурации, в которой w записана во входной очереди, распознаватель может выполнить последовательность тактов, завершающуюся конечной конфигурацией.

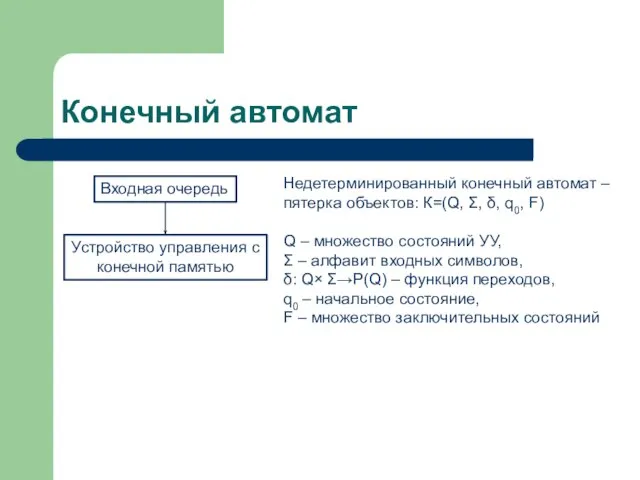
Конечный автомат
Входная очередь
Устройство управления с конечной памятью
Недетерминированный конечный автомат – пятерка объектов: К=(Q, Σ, δ, q0, F)
Q – множество состояний УУ,
Σ – алфавит входных символов,
δ: Q× Σ→P(Q) – функция переходов,
q0 – начальное состояние,
F – множество заключительных состояний

Конечные преобразователи
Входная очередь
Устройство управления с конечной памятью
Выходная очередь
Такт работы конечного преобразователя – переход от конфигурации (q, ax, y) к конфигурации (r, x, yz), если δ(q,a) содержит (r, z).
Недетерминированный конечный преобразователь – шестерка объектов: К=(Q, Σ, Δ, δ, q0, F)
Q – множество состояний УУ,
Σ – алфавит входных символов,
Δ – алфавит выходных символов
δ: Q× Σ→P(Q) × Δ – функция переходов,
q0 – начальное состояние,
F – множество заключительных состояний
Конфигурация конечного преобразователя - тройка (q, ax, y),
где q – состояние, x – необработанная часть входной цепочки,
y – построенная часть выходной цепочки.

Регулярный перевод
Формализация такта КП как отношения ├ на множестве конфигураций:
Для всех q∈Q, а∈Σ, х∈Σ и у∈Δ, таких, что δ(q, a) содержит (r, z),
конфигурации (q, ax, y) ├ (r, x, yz).
Транзитивное замыкание отношения├ обозначим ├+
Рефлексивно-транзитивное замыкание отношения├ обозначим ├*
Цепочка у∈Δ называется выходом для цепочки х∈Σ, если (q0, x, ε) ├* (q, ε, y)
для некоторого q из множества конечных состояний.
Переводом, определяемым конечным преобразователем, называется множество пар цепочек:
τ(М) = { (x, y) | (q0, x, ε) ├* (q, ε, y) для некоторого q∈F}
(регулярный, или конечный, перевод)

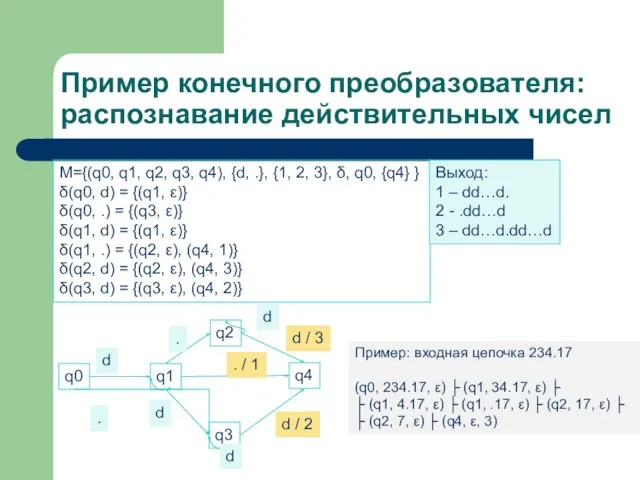
Пример конечного преобразователя: распознавание действительных чисел
М={(q0, q1, q2, q3, q4), {d, .}, {1, 2, 3}, δ, q0, {q4} }
δ(q0, d) = {(q1, ε)}
δ(q0, .) = {(q3, ε)}
δ(q1, d) = {(q1, ε)}
δ(q1, .) = {(q2, ε), (q4, 1)}
δ(q2, d) = {(q2, ε), (q4, 3)}
δ(q3, d) = {(q3, ε), (q4, 2)}
Выход:
1 – dd…d.
2 - .dd…d
3 – dd…d.dd…d
q0
q1
q2
q3
q4
d
d / 3
d / 2
d
d
d
.
.
. / 1
Пример: входная цепочка 234.17
(q0, 234.17, ε) ├ (q1, 34.17, ε) ├
├ (q1, 4.17, ε) ├ (q1, .17, ε) ├ (q2, 17, ε) ├
├ (q2, 7, ε) ├ (q4, ε, 3)

Конфигурация
МП-автомата
(q, х, Z):
q∈Q – состояние УУ
х ∈ Σ* - необработанная часть входной цепочки
Z ∈ Г* - содержимое магазина (левый символ – вершина стека)
Автомат с магазинной памятью
Входная очередь
Устройство управления с конечной памятью
Z
α
Z0
магазин (стек)
Такт работы МП-автомата:
переход от конфигурации (q, aw, Z) к конфигурации (r, w, γα), если δ(q, a, Z) содержит (r, γ).
(q, aw, Z) ├ (r, w, γα)
МП-автоматом называется семерка
P = (Q, Σ, Г, δ, q0, Z0, F), где
Q – множество состояний УУ
- алфавит входных символов
Г – алфавит выходных символов
- функция переходов: Q×(Σ∪{ε})×Г→Q×Г*
q0 – начальное состояние УУ
Z0 – начальный символ (дно) магазина
F – множество заключительных состояний

Пример: МП-автомат для распознавания симметричных цепочек
P = ({q0, q1, q2}, {a, b}, {Z, a, b}, δ, q0, Z, {q2})
Функции переходов:
δ(q0, a, Z)={(q0, aZ)}
δ(q0, b, Z)={(q0, bZ)}
δ(q0, a, a)={(q0, aa), (q1, ε)}
δ(q0, a, b)={(q0, ab)}
δ(q0, b, a)={(q0, ba)}
δ(q0, b, b)={(q0, bb), (q1, ε)}
δ(q1, a, a)={(q1, ε)}
δ(q1, b, b)={(q1, ε)}
δ(q1, ε, Z)={(q2, ε)}
Примеры:
(q0, baab, Z) ├ (q0, aab, bZ) ├
├ (q0, ab, abZ) ├ (q1, b, bZ) ├
├ (q1, ε, Z) ├ (q2, ε)
(q0, baab, Z) ├ (q0, aab, bZ) ├
├ (q0, ab, abZ) ├ (q0, b, aabZ) ├
├(q0, ε, baabZ) – ошибка

Расширенный МП-автомат
Лемма:
Если (q, w, A) ├n (q’, ε, ε), то (q, w, Aα) ├ n (q’, ε, α) для всех A∈Γ и α∈Γ*.
Расширенным МП-автоматом называется МП-автомат, который за один такт может заменять цепочку конечной длины в вершине магазина другой цепочкой конечной длины.
Функция переходов δ: Q×(Σ∪{ε})×Г*→Q×Г*
Пример расширенного МП-автомата для языка wwR
P = ({q0, q1}, {a, b}, {S, Z, a, b}, δ, q0, Z, {q1})
Функции переходов:
δ(q0, a, ε)={(q0, a)}
δ(q0, b, ε)={(q0, b)}
δ(q0, ε, ε)={(q0, S)}
δ(q0, ε, aSa)={(q0, S)}
δ(q0, ε, bSb)={(q0, S)}
δ(q0, ε, SZ)={(q1, ε)}

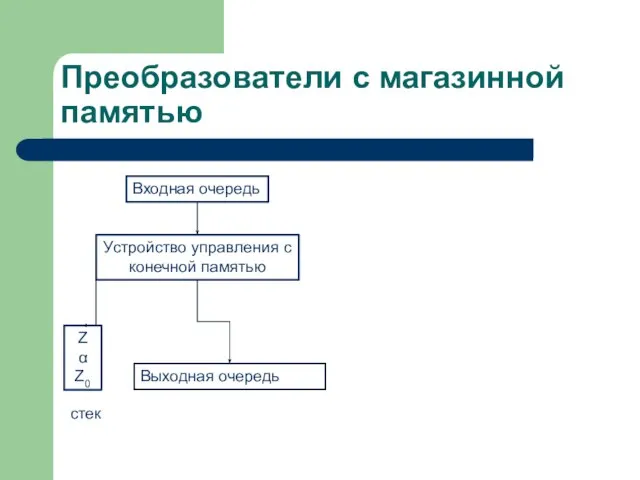
Преобразователи с магазинной памятью
Входная очередь
Устройство управления с конечной памятью
Z
α
Z0
стек
Выходная очередь

Размеченный вывод цепочек в КС-грамматике
Грамматика:
(1)
(2)
(3)
(4)
(5)
(6)
Предложение: i+i*i
Левый вывод:
E=>(1) E+T=>(2) T+T=>(4) P+T=>
=>(5) i+T=>(3) i+T*P=>
=>(4) i+P*P=>(5) i+i*P=>(5) i+i*i
Правый вывод:
E=>(1) E+T=>(3) E+T*P=>(5) E+T*i=>
=>(4) E+P*i=>(5) E+i*i=>(2) T+i*i=>
=>(4) P+i*i=>(5) i+i*i

Дерево вывода
Упорядоченное дерево, каждый узел которого помечен символом из
, называется деревом вывода в КС-грамматике G=(N,Σ, P, S),
если:
Корень дерева помечен основным символом грамматики S.
Каждый прямой потомок узла, помеченного символом А, помечен таким символом Х, что грамматика содержит правило вывода А→Х.
3. Если узел Di помечен символом Хi из N, то поддерево Di должно быть деревом вывода в грамматике Gi=(N,Σ, P, Хi).
4. Если Хi - символ из Σ, то поддерево Di состоит из одной вершины, помеченной Хi
5. Если корень дерева состоит из единственного потомка, помеченного ε, то этот потомок образует дерево, состоящее из единственной вершины, и в множестве правил грамматики содержится правило S→ε.

Определение разбора
Цепочка для КС-грамматики разобрана, если известно её дерево вывода.
Пусть заданы КС-грамматика G, правила которой перенумерованы целыми числами 1, 2, …, р, и цепочка терминальных символов α. Тогда:
левым разбором цепочки α называется последовательность правил, примененных при её левом выводе из S;
правым разбором цепочки α называется обращение последовательности правил, примененных при правом выводе цепочки из S.

Эквивалентность КС-грамматик и МП-автоматов
Пусть G=(N,Σ, P, S) – КС-грамматика,
P =({q}, Σ, ΣᵕN, δ, q, S, {q}) – МП-автомат с правилами перехода δ :
Если А→α - правило вывода грамматики G, то δ(q, ε, A) содержит (q, α)
δ(q, a, a) = {(q, ε)} для всех а из Σ.
Тогда А=>m w тогда и только тогда, когда (q, w, A)├ n (q, ε, ε) для некоторых m, n.
Лемма о нисходящем разборе

Пример: МП-автомат для скобочных выражений
Грамматика:
G=({E, T, M}, {i, +, *, (, )}, {E→E+T, E→T, T→T*M, T→M, M→(E), M→i}, E)
МП-автомат:
P=({q}, {i, +, *, (, ), E, T, M}, δ, q, E, {q})
с правилами перехода:
1) δ(q, ε, E)={(q, E+T), {(q,T)}}
2) δ(q, ε, T)={(q, T*M), {(q,M)}}
3) δ(q, ε, M)={(q, (E) ), {(q,i)}}
4) δ(q, a, a)={(q, ε)} для всех a из {i, +, *, (, )}

Пример: разбор цепочки i*(i+i)
(q, i*(i+i), E)├ (q, i*(i+i), T)├ (q, i*(i+i), T*M)
├ (q, i*(i+i), i*M)├ (q, *(i+i), *M) ├ (q, *(i+i), *M)
├ (q, (i+i), M)├ (q, (i+i), (E) )├ (q, i+i), E) )├ (q, i+i), E+T) )
├(q, i+i), T+T) )├(q, i+i), M+T) )├(q, i+i), i+T) )
├ (q, +i), +T) )├ (q, i), T) )├(q, i), M) )├ (q, i), i) )
├ (q, ), ) )├ (q, ε, ε)
Последовательность тактов МП-автомата соответствует левому выводу цепочки i*(i+i) в грамматике G.

Восходящий синтаксический анализ (свертка слева)
Правый вывод цепочки i+i*i:
E=>(1) E+T=>(3) E+T*P=>(5) E+T*i =>(4) E+P*i=>(5) E+i*i=>(2) => T+i*i=>(4) P+i*i=>(5) i+i*i
Обращение правого вывода цепочки i+i*i:
i+i*i <= P+i*i <= T+i*i <= E+i*i <= E+P*i <= E+T*i <= E+T*P <= E+T <= E
Пусть G – КС-грамматика, S=>αAw=>αβw=>xw – правый вывод в ней.
Правовыводимую цепочку αβw можно свернуть слева к правовыводимой цепочке αAw с помощью правила вывода A→β. Это вхождение цепочки β в цепочку αβw называется основой цепочки αβw.
Пример: правила вывода {S→Ac, S →Bd, A →aAb, A →ab, B →aBbb, B →abb}.
Цепочка aabbbbd – правовыводимая, abb – основа этой цепочки (т.к. abb – правая часть правила B →abb и aBbbd – правовыводимая цепочка.
Цепочка ab – не основа, т.к. это правая часть правила A →ab, но aAbbbd – не правовыводимая цепочка.