Задача размещения

Задачи размещения связаны с решением проблем наилучшего расположения в определенных регионах таких систем обслуживания, как торговые центры, посты пожарной охраны, фабрики, аэропорты, склады и т. д. Математическая структура задачи размещения определяется конфигурацией области допустимых точек и способом оценки качества размещения. Вследствие этого существует много разнообразных задач размещения, и техническая литература изобилует методами их решения. В этом разделе мы ограничимся рассмотрением только таких задач размещения, для которых областью допустимых точек размещения центров обслуживания является некоторый граф, т. е. эти центры могут располагаться в какой-либо вершине или на какой-либо дуге графа.

В задачах размещения есть два основных критерия оценки качества размещения: минимизация максимального расстояния и минимизация суммы расстояний. Соответственно имеем и две основные задачи. Задача поиска точки размещения, выбранной в соответствии с критерием минимизации максимального расстояния, называется задачей поиска центра графа, точки выбранной по критерию минимизации суммы расстояний – задачей поиска медианы.
Прежде чем ввести более строгие определения подлежащих рассмотрению различных типов размещений, следует ввести некоторые определения, необходимые для описания точек на дугах и различных расстояний в графе.

Множество рассматриваемых вершин в графе содержит вершины с номерами от 1 до n. Рассмотрпм произвольную дугу (i, j), длина которой равна ai,j>0. Пусть f обозначает точку на дуге (i, j), которая для всех 0≤f≤1 отстоит на f×ai,j единиц от вершины i и на (1 — f)×ai,j единиц от вершины j. Назовем ее f-точкой. Таким образом, четверть-точкой дуги (i, j) является точка, отстоящая от вершины i на 1/4 длины дуги (i, j)
Нуль-точка дуги (i, j) является вершиной i, а единичная точка дуги (i, j) — вершиной j. Следоватльно, вершины графа также могут рассматриваться как точки дуг. Точки дуг, которые не являются вершинами, называются внутренними точками. Любая точка дуги должна быть либо внутренней точкой, либо вершиной. Как и ранее, обозначим через Х множество всех вершин графа. Пусть через Р обозначается множество всех точек. Таким образом, Р — Х является множеством всех внутренних точек.

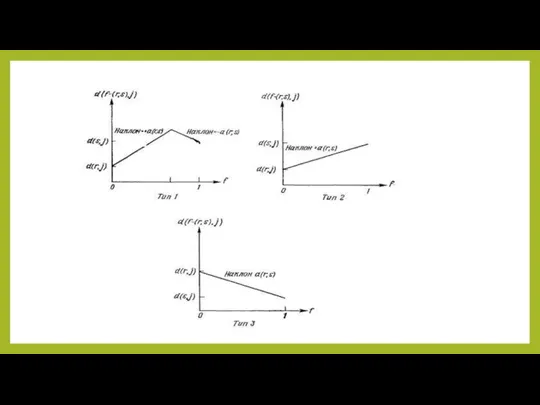
Пусть di,j обозначает длину кратчайшего пути из вершины i в вершину j. Тогда через D обозначается матркца n×n, в которой элементом (i, j) является di,j. Элементы в матрице называются расстоянимми вершина — вершина. Напомним, что для вычисления элементов матрицы 1 может быть использован любой из двух рассмотренных ранее алгоритмов: алгоритм Флойда или алгоритм Данцига. Пусть через d(f -(r,s ), j) обозначена длина кратчайшего пути от f-точки на дуге (r,s) до вершины j. Эта величина называется расстоянием точка — вершина. Если дуга (r,s) неориентированная, т. е. допустим ее обход в обоих направлениях, то в качестве d(f -(r,s ), j) должно быть выбрано паименьшее из следующих двух расстояний:
(а) расстояние от точки до вершины r плюс расстояние от вершины f до вершины j,
(б) расстояние от f-точки до вершины s плюс расстояние от вершины s до вершины j.
Таким образом,
d(f—(r,s ),j)=min{f×аr,s+dr,j), (1—f)×аr,s+ds,j}. (1a)
Если дуга (r,s) ориентированная, т. е. ее обход допустим только из r в s, то первый член в (1а) может быть исключен и
d(f—(r,s ),j) =(1—f)×аr,s+ds,j . (1б)

Заметим, что для вычисления всех расстояний точка — вершина необходимо знать только значения длин всех дуг и значения всех элементов матрицы D.
Для заданной дуги (r,s) и вершины j расстояние точка — вершина как функция от f на графике должна иметь один из трех типов зависимостей, показанных на рисунке Заметим, что угол наклона этой кусочно-лпнейной кривой равен +аr,s или -аr,s и его величина может не более одного раза измениться от +аr,s до -аr,s.

Условные Обозначения

Рассматривается вопрос о строительстве поликлиники. Существуют три возможных района строительства: А, В, С. Все данные отражены в таблице.
РЕШЕНИЕ ЗАДАЧИ

Периодичность возобновления поставок
Дадим рекомендации о месте строительства, используя метод взвешивания. Заполним таблицу.

Суммарные годовые затраты
Поясним, как заполняется таблица.
Числа 2-го столбца умножаем на числа 3-го (4-го) столбца соответственно и результат пишем в 6-м (7-м) столбце. 8-й столбец равен произведению 2-го и 5-го столбцов.
В последней строке указана сумма чисел соответствующего столбца.
Вариант с наибольшей суммой (7,1) — это строительство поликлиники в районе А.