возник вокруг исследований о функциях. Раздор о первенстве в получении результатов привлек внимание всей общественности своего времени. Но было ли место для конфликта? Сегодня достоверно известно, что нет. Ведь каждый из них шел своим путем, и лишь один Бог ведает, как сильно могла уйти вперед наука, если бы эти мыслители встретились тогда в далеком прошлом.
великих деятелях, как сэр Исаак Ньютон и Готфрид Вильгельм фон Лейбниц. Конфликт возник вокруг исследований о функциях. Раздор о первенстве в получении результатов привлек внимание всей общественности своего времени. Но было ли место для конфликта? Сегодня достоверно известно, что нет. Ведь каждый из них шел своим путем, и лишь один Бог ведает, как сильно могла уйти вперед наука, если бы эти мыслители встретились тогда в далеком прошлом.
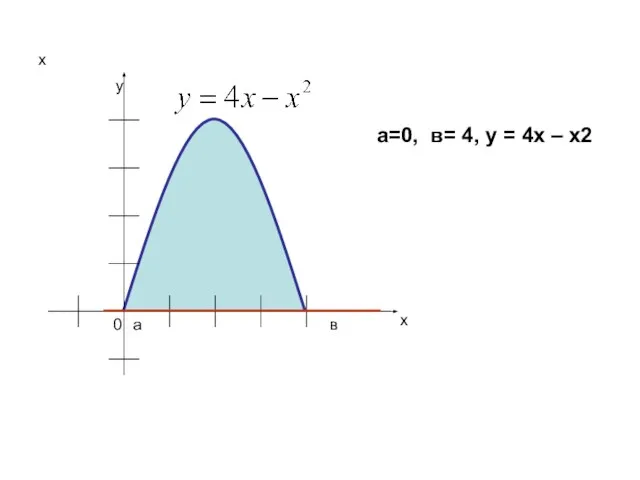
![Определение: фигура, ограниченная графиком неотрицательной и непрерывной на отрезке [a; b] функции](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/429002/slide-1.jpg)
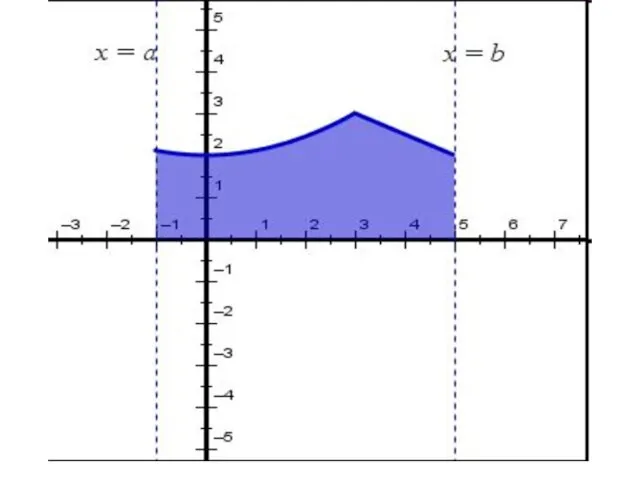
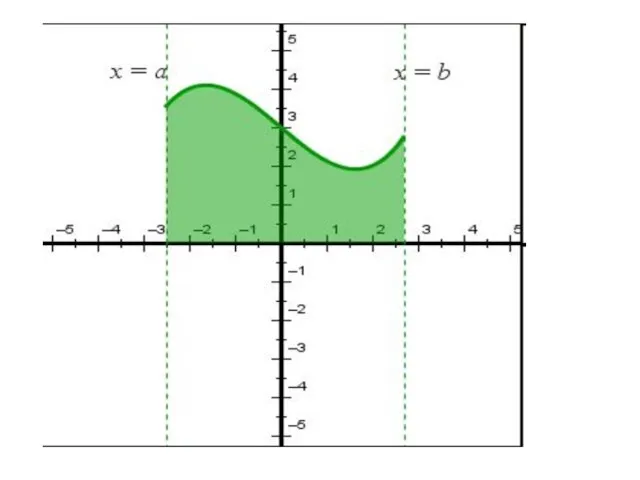
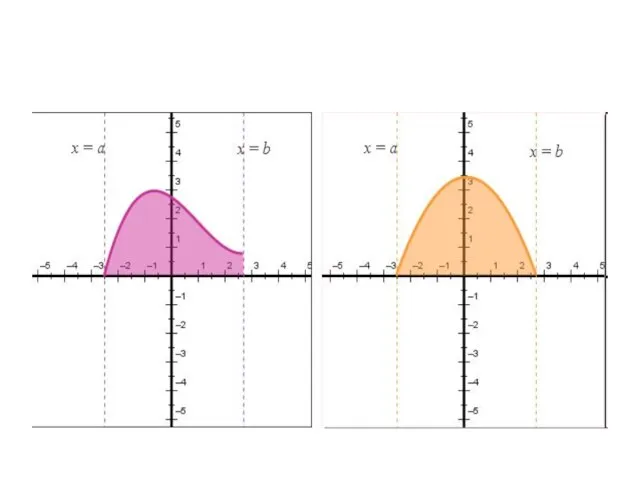
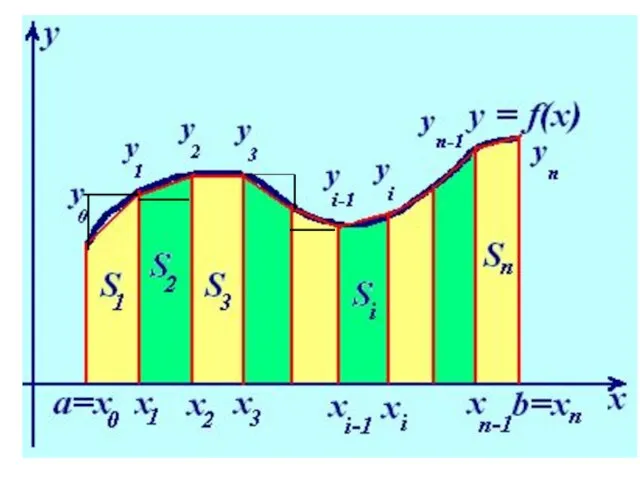

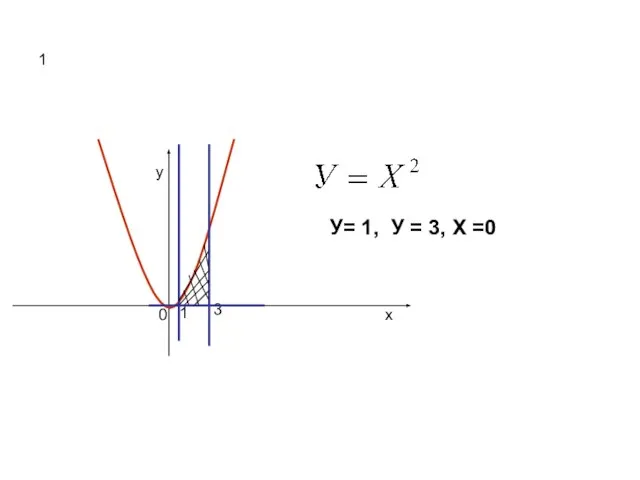
![Понятие определенного интеграла. 1. Разбиваем отрезок [а;в] на nравных частей. 2. Составляем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/429002/slide-7.jpg)


![Формула Ньютона- Лейбница Если f(х)– непрерывная и неотрицательная на отрезке [a; b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/429002/slide-10.jpg)


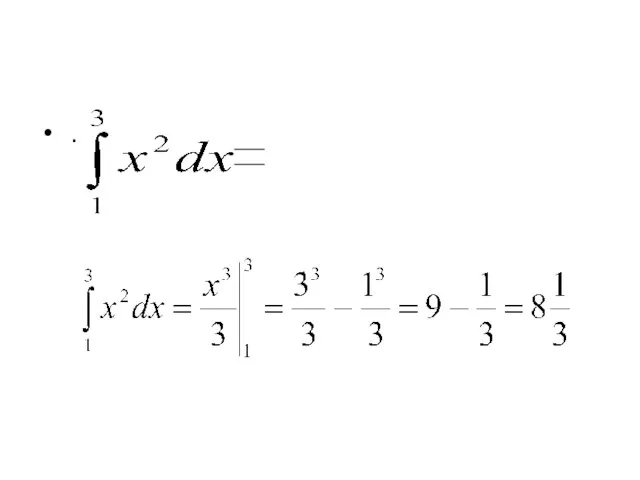

 Talk for a minute
Talk for a minute Литературная игра для младших школьников по произведениям Н.Н.Носова «Затейники и фантазёры»
Литературная игра для младших школьников по произведениям Н.Н.Носова «Затейники и фантазёры» L`italiano è facile
L`italiano è facile Коммуникации. Техника 3-х касаний
Коммуникации. Техника 3-х касаний Муниципальное образовательное учреждение "Ковылкинская средняя общеобразовательная школа № 1"
Муниципальное образовательное учреждение "Ковылкинская средняя общеобразовательная школа № 1" Грант 2013г
Грант 2013г Тема урока: «Бунташный век».
Тема урока: «Бунташный век». History & Mystery of the English language
History & Mystery of the English language Внутренняя среда организма. Кровеносная система
Внутренняя среда организма. Кровеносная система Современные средства поражений
Современные средства поражений ПЕРСПЕКТИВНАЯ НАЧАЛЬНАЯШКОЛА
ПЕРСПЕКТИВНАЯ НАЧАЛЬНАЯШКОЛА lecture_1
lecture_1 Тукай начал изучать русский язык
Тукай начал изучать русский язык История праздника Новый Год
История праздника Новый Год Проект: видеоблог
Проект: видеоблог Расчет теплоусвоения внутренней поверхности полов
Расчет теплоусвоения внутренней поверхности полов ЭФФЕКТ КАЗИМИРА: ОТ НАНОТЕХНОЛОГИЙ ДО ФИЗИКИ ВСЕЛЕННОЙ
ЭФФЕКТ КАЗИМИРА: ОТ НАНОТЕХНОЛОГИЙ ДО ФИЗИКИ ВСЕЛЕННОЙ Цифровые права
Цифровые права Сетевой маркетинг
Сетевой маркетинг культура и достопримечательности Греции
культура и достопримечательности Греции Мектеп бітірушілердің психологиялық-физиологиялық жағдайын ескере отырып қобалжу деңгейін төмендету
Мектеп бітірушілердің психологиялық-физиологиялық жағдайын ескере отырып қобалжу деңгейін төмендету Решение текстовых задач. Закрепление пройденного
Решение текстовых задач. Закрепление пройденного Традиционная реклама
Традиционная реклама Saint Patricks day
Saint Patricks day КОМПЬЮТЕРНАЯ ДОЛИНА
КОМПЬЮТЕРНАЯ ДОЛИНА Литературная игра по творчеству А.С. Пушкина
Литературная игра по творчеству А.С. Пушкина Презентация на тему Семейство Губоцветные
Презентация на тему Семейство Губоцветные ФИЗИЧЕСКАЯ КУЛЬТУРА
ФИЗИЧЕСКАЯ КУЛЬТУРА