Слайд 2«Если написанная программа сработала правильно, то это значит, что во время её

работы выполнилось чётное число ошибок»
Правило чётности ошибок
Слайд 3ЦЕЛЬ:
углубить и расширить свои знания в области решения задач на чётность.

Слайд 4ЗАДАЧИ:
Изучить литературу по данной теме;
Классифицировать задачи;
Совершенствовать навыки решения задач на чётность и

нечётность.
Слайд 5Формула чётного числа – 2 с
Формула нечётного числа – 2с+1

Слайд 6КЛАССИФИКА-ЦИЯ ЗАДАЧ
АРИФМЕТИКА ЧЁТНОСТИ
ЧЕРЕДОВАНИЕ
РАЗБИЕНИЕ НА ПАРЫ
Слайд 7Задача:
На 99 карточках пишут числа 1,2,…,99, перемешивают их, раскладывают чистыми сторонами вверх

и снова пишут числа 1,2,…,99. Для каждой карточки складывают два числа и 99 полученных сумм перемножают. Докажите, что результат чётен.
Слайд 8Нечётные числа – 1,3,…,99;
всего – 50 чисел.
Чётные числа –
2,4,…,98;
всего – 49.

Слайд 9Задача:
Прямая пересекает все стороны шестиугольника. Может ли прямая пересекать все стороны

какого-нибудь 17-угольника, не проходя ни через одну его вершину
Слайд 11Задача:
Денис хочет написать на доске 51 различное двузначное число так, чтобы среди

них не было двух чисел, дающих в сумме 100. Сможет ли он это сделать?
Слайд 12Двузначные числа – 10,11,…,99;
всего – 90 чисел.
Кроме чисел 50, 91, 92,…, 99

(10 штук), все остальные разбиваются на 40 пар чисел, дающих в сумме 100. Следовательно, получится взять не более 50 чисел.
Слайд 13Игры-шутки
На доске написаны 6 единиц и 6 двоек. За ход разрешается стереть

две любые цифры и, если они были одинаковыми, написать двойку, а если разными – единицу. Если последняя оставшаяся на доске цифра – единица, то выиграл первый игрок, если двойка – то второй.
Слайд 14Выводы:
Наблюдение может привести к открытию;
Лучший способ изучить что-либо – открыть это самому;

Можно обнаружить общий метод;
Развивают смекалку и сообразительность, умение ставить вопросы, отвечать на них;
Приучают к самостоятельной работе;
Слайд 15Выводы:
Развивают умение анализировать задачные ситуации, строить план решения;
Воспитывают логическую культуру;
Обогащают

опыт мыслительной деятельности;
Способствуют глубокому пониманию школьной программы и расширению кругозора.
Слайд 16Приобретать знания – храбрость,
Приумножать их – мудрость,
А умело применять великое искусство.
















 И.И Лажечников
И.И Лажечников Контрольная работа. Распределение вариантов
Контрольная работа. Распределение вариантов Как преодолеть застенчивость и неуверенность ребёнка?
Как преодолеть застенчивость и неуверенность ребёнка? Історія розвитку фірми Sun
Історія розвитку фірми Sun Воспитай отличника!
Воспитай отличника! Самой красивой женщине в мире (стихотворения)
Самой красивой женщине в мире (стихотворения) Типология обществ (8 класс)
Типология обществ (8 класс) Работа - как жизненный путь
Работа - как жизненный путь Управление и менеджмент
Управление и менеджмент Оборудование системы тепло- и холодоснабжения
Оборудование системы тепло- и холодоснабжения Презентация на тему ЛИВОНСКАЯ ВОЙНА ИСТОРИЯ
Презентация на тему ЛИВОНСКАЯ ВОЙНА ИСТОРИЯ  Методы диагностики детей и подростков, склонных к асоциальному поведению
Методы диагностики детей и подростков, склонных к асоциальному поведению Диаграмма кооперации
Диаграмма кооперации Суриков Василий Иванович великий художник XIX века
Суриков Василий Иванович великий художник XIX века Классицизм
Классицизм ЖратьСтвуйте!
ЖратьСтвуйте! Фотоотчет распространения промотиража газеты Маяк
Фотоотчет распространения промотиража газеты Маяк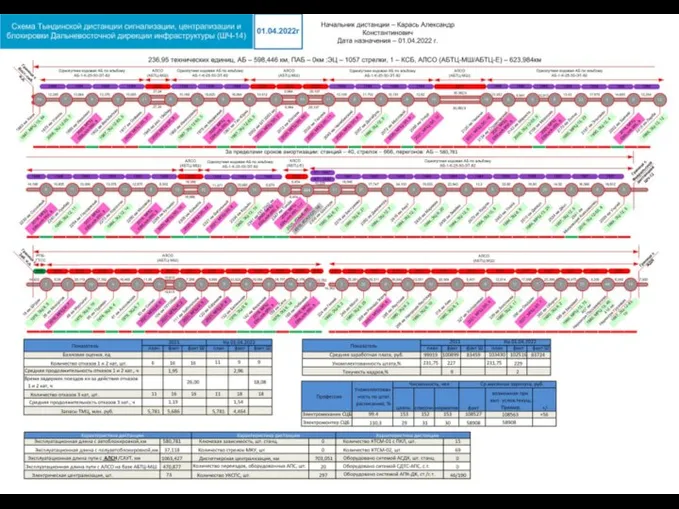 ШЧ-14 на 01 09 22
ШЧ-14 на 01 09 22 French cuisine
French cuisine  Род Толстых существовал в России 600 лет до рождения Льва Николаевича и существует поныне.
Род Толстых существовал в России 600 лет до рождения Льва Николаевича и существует поныне. Система школьного самоуправления
Система школьного самоуправления Оценка компонентов культуры обслуживания предприятия сервиса (на примере пиццерии Pizza Mia)
Оценка компонентов культуры обслуживания предприятия сервиса (на примере пиццерии Pizza Mia) Презентация на тему Округление десятичных чисел
Презентация на тему Округление десятичных чисел  Трудные случаи таблицы умножения и деления
Трудные случаи таблицы умножения и деления Информационные технологии – оружие России
Информационные технологии – оружие России Буквы К, к, обозначающие согласные звуки [к], [к`]
Буквы К, к, обозначающие согласные звуки [к], [к`] Сумо. Ритуалы и правила сумо
Сумо. Ритуалы и правила сумо Презентация на тему Нью-Йорк
Презентация на тему Нью-Йорк