Содержание
- 2. Для решения многих геометрических задач, связанных с тетраэдром и параллелепипедом, полезно уметь строить на рисунке их
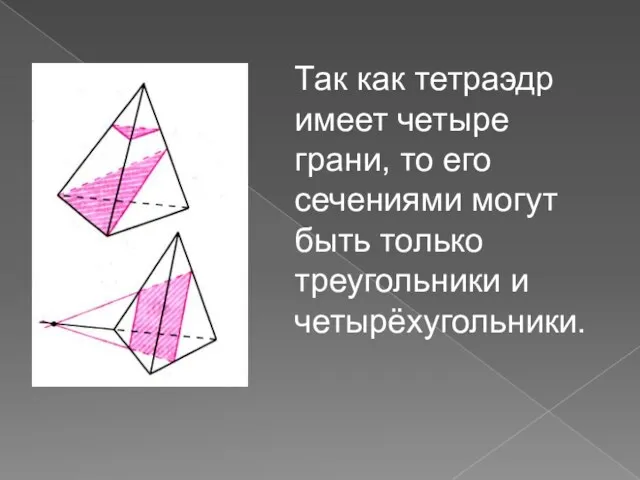
- 3. Так как тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники и четырёхугольники.
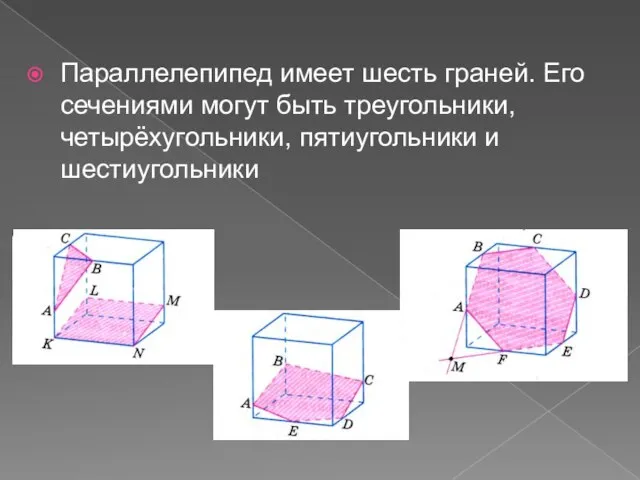
- 4. Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырёхугольники, пятиугольники и шестиугольники
- 5. При построении сечений параллелепипеда следует учитывать тот факт, что если секущая плоскость пересекает две противоположные грани
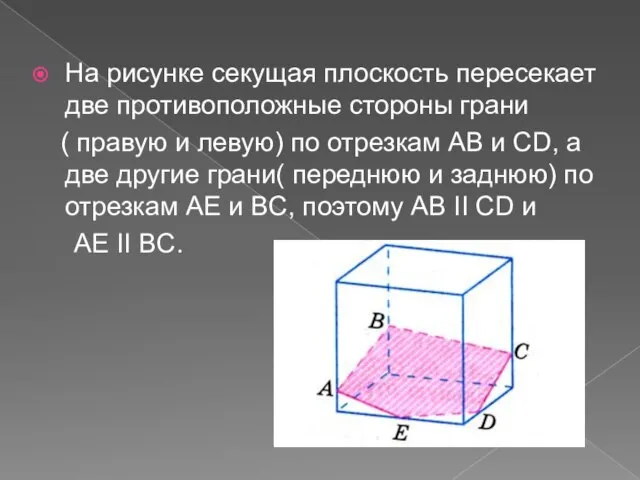
- 6. На рисунке секущая плоскость пересекает две противоположные стороны грани ( правую и левую) по отрезкам AB
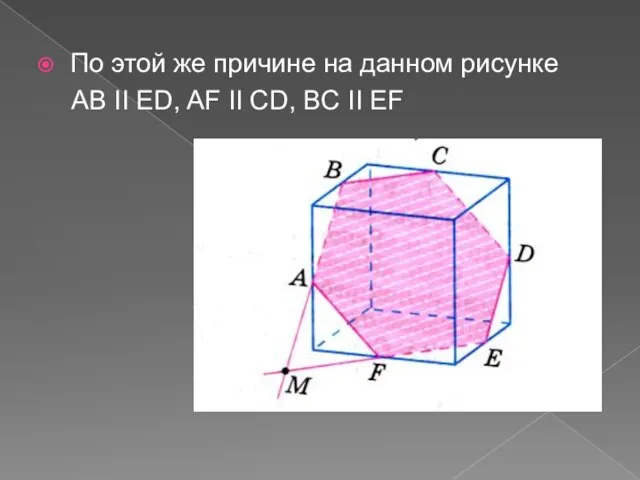
- 7. По этой же причине на данном рисунке AB II ED, AF II CD, BC II EF
- 8. Для построения сечения достаточно построить точки пересечения секущей плоскости с ребрами тетраэдра (параллелепипеда), после чего останется
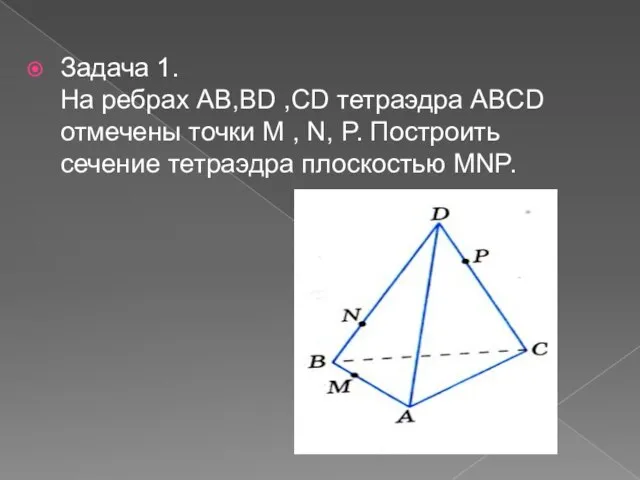
- 9. Задача 1. На ребрах АВ,BD ,CD тетраэдра ABCD отмечены точки M , N, P. Построить сечение
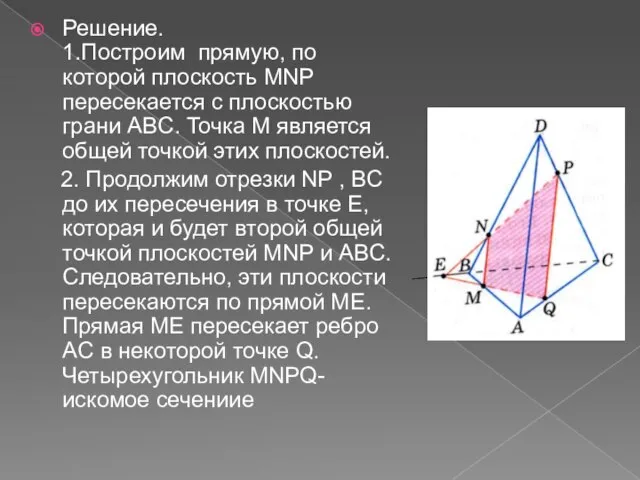
- 10. Решение. 1.Построим прямую, по которой плоскость MNP пересекается с плоскостью грани ABC. Точка M является общей
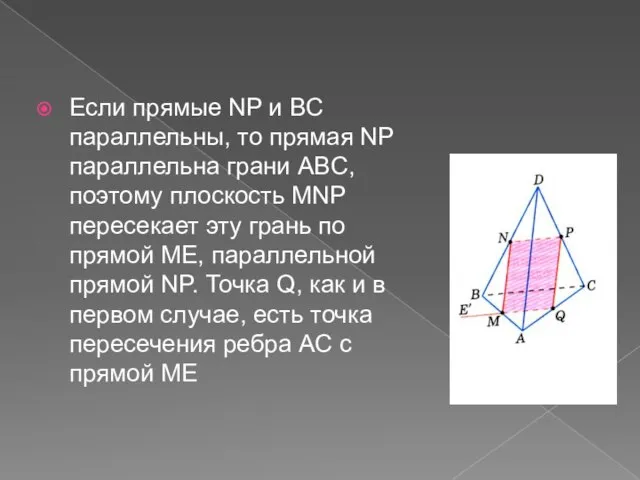
- 11. Если прямые NP и BC параллельны, то прямая NP параллельна грани ABC, поэтому плоскость MNP пересекает
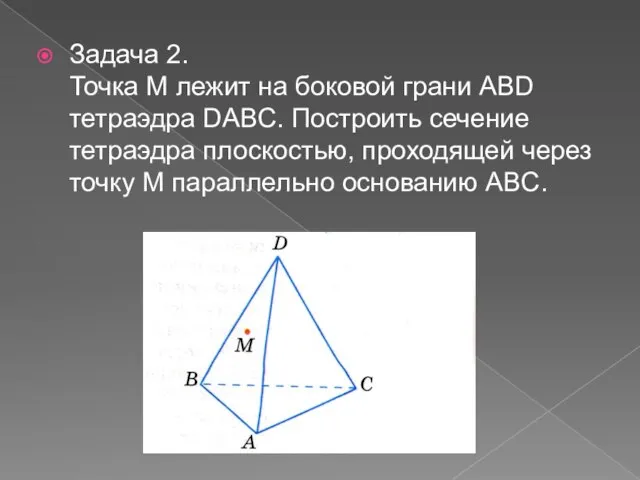
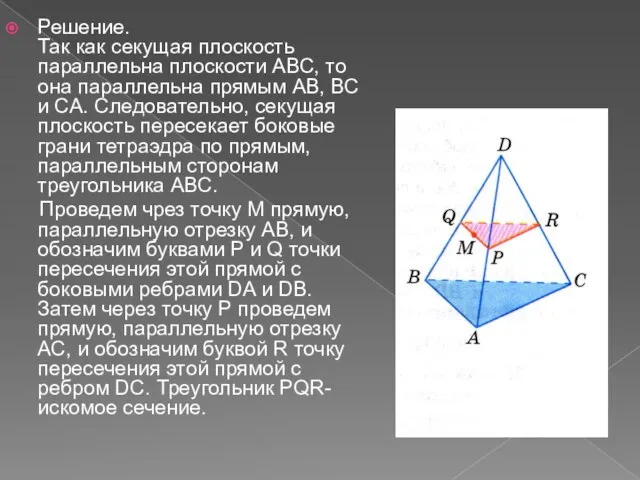
- 12. Задача 2. Точка M лежит на боковой грани ABD тетраэдра DABC. Построить сечение тетраэдра плоскостью, проходящей
- 13. Решение. Так как секущая плоскость параллельна плоскости АВС, то она параллельна прямым АВ, ВС и СА.
- 14. Задача 3 . На ребрах параллелепипеда даны три точки А, В и С. Построить сечение параллелепипеда
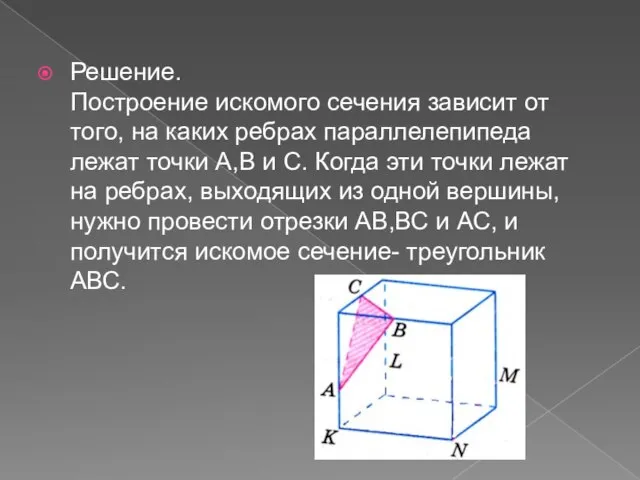
- 15. Решение. Построение искомого сечения зависит от того, на каких ребрах параллелепипеда лежат точки А,В и С.
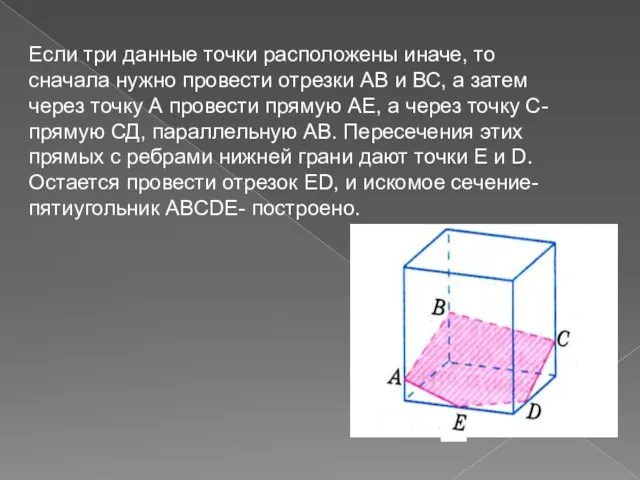
- 16. Если три данные точки расположены иначе, то сначала нужно провести отрезки АВ и ВС, а затем
- 18. Скачать презентацию




 Примерный эскиз баннера. Kronomir
Примерный эскиз баннера. Kronomir Глава 3. Экономика фирмы
Глава 3. Экономика фирмы Гончарова Ирина Алексеевна
Гончарова Ирина Алексеевна Оценка стоимости бренда
Оценка стоимости бренда Латинская Америка
Латинская Америка Психологическая служба школы«Ни себя, нм других нельзя изучать иначе как в деятельности и общении. Нельзя изучать человека холод
Психологическая служба школы«Ни себя, нм других нельзя изучать иначе как в деятельности и общении. Нельзя изучать человека холод Необычные факты о птицах
Необычные факты о птицах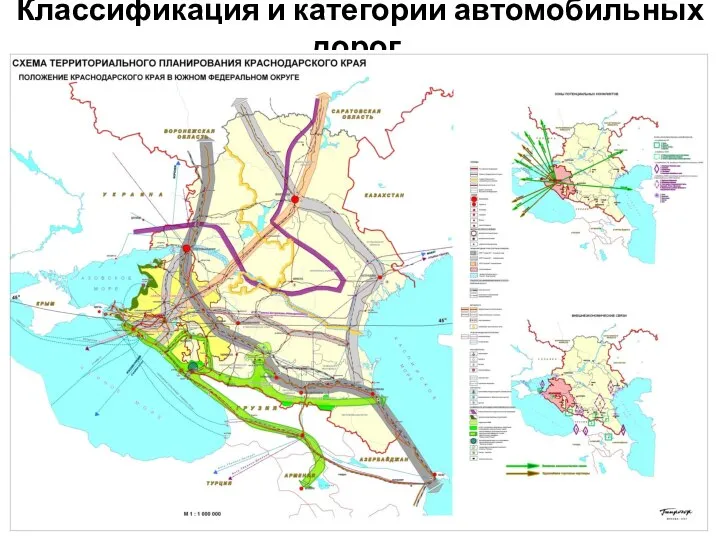 Классификация и категории автомобильных дорог
Классификация и категории автомобильных дорог Этикет 4 класс
Этикет 4 класс Влияние вредных привычек на сердечно-сосудистую и дыхательную системы
Влияние вредных привычек на сердечно-сосудистую и дыхательную системы Воля. Виды и содержания волевых процессов
Воля. Виды и содержания волевых процессов Э-74 Против курения
Э-74 Против курения Агентство по ипотечному жилищному кредитованию
Агентство по ипотечному жилищному кредитованию Возрождение Руси. Иван Калита
Возрождение Руси. Иван Калита Растительные сообщества и взаимосвязи в них
Растительные сообщества и взаимосвязи в них Чтение слов и предложений с буквой Ц
Чтение слов и предложений с буквой Ц Презентация на тему Древние германцы и Римская империя
Презентация на тему Древние германцы и Римская империя  Системный анализ предметной области кандидатской диссертации
Системный анализ предметной области кандидатской диссертации School subjects
School subjects Архимедова сила (7 класс)
Архимедова сила (7 класс) Здравствуй, милая картошка!
Здравствуй, милая картошка! Три среды обитания. Наземно-воздушная среда
Три среды обитания. Наземно-воздушная среда Формованный эластичный ППУ для автомобильной промышленности
Формованный эластичный ППУ для автомобильной промышленности Расшифровка моделей Indesit
Расшифровка моделей Indesit Выполнение эскиза в точечной технике
Выполнение эскиза в точечной технике Особенности питания студентов
Особенности питания студентов Портфолио педагога
Портфолио педагога Воспитательные традиции в системе дополнительного образования
Воспитательные традиции в системе дополнительного образования