"Задачи планиметрии в ЕГЭ"

Единый Государственный Экзамен по математике значительно отличается от выпускного экзамена, который проводится в школе по окончании 11 класса. Это отличие прежде всего состоит в том, что ЕГЭ совмещает два экзамена- выпускной школьный и вступительный в вуз.
Поэтому при подготовке к сдаче ЕГЭ необходимо повторить материал не только курса “Алгебры и начал анализа” , но и некоторых разделов курса математики основной и средней школы, в том числе и планиметрии.
Геометрические задания из курса планиметрии содержатся во второй части ЕГЭ (задания с кратким свободным ответом ).
Следует заметить, что с решением геометрических задач справляются далеко не многие.
Рассмотрим некоторые планиметрические задачи.

Задача №1.
Основания равнобедренной трапеции равны 3м и
8м, а угол при основании 60º.
Найдите диагональ.
Дано:
АВСD- трапеция,
AD=BC,AB=3м,CD=8м,
Найти: АС.

Решение:
Трапеция равнобедренная →AC=BD, < C =
Пусть АК║ВС. Так как АВ║CD (основания трапеции), то АВСК- параллелограмм. Тогда КС=АВ=3м, DК=8-3=5м, ВС=АК=АD.
В треугольнике АDК: AD=AK, →
В треугольнике АВС АС²=АВ²+ВС²-2АВ·ВС·cos <В
т.е. АС²=3²+5²-2·3·5·cos120º=49.
(теорема косинусов),
Итак, АС=7м.
Ответ: 7м.

Задача №2.
Окружность, вписанная в равнобедренный треугольник
АВС с основанием АС, касается сторон АВ и ВС в точках К и М соответственно. Найдите КМ, если АК=6м, КВ=12м.
Дано:
Треугольник АВС,
АВ=ВС, АК=6м, ВК=12м,
К, М и Т- точки касания вписанной окружности.
Найти: КМ.

Решение:
По условию ВС= АВ= 6+12=18(м).
ВМ=ВК=12м (отрезки касательных, проведённых из одной точки), → СМ=18-12=6(м).
3. АТ=АК=6м, СТ=СМ=6м (отрезки касательных, проведённых из одной точки)→АС=6+6=12(м).
4. ∆КВМ и ∆АВС- подобны (<В- общий, ВК:АВ=ВМ:ВС)→КМ:АС=ВК:АВ, т.е.
КМ:12=12:18, КМ= 12·12:18=8(м).
Ответ: 8м.

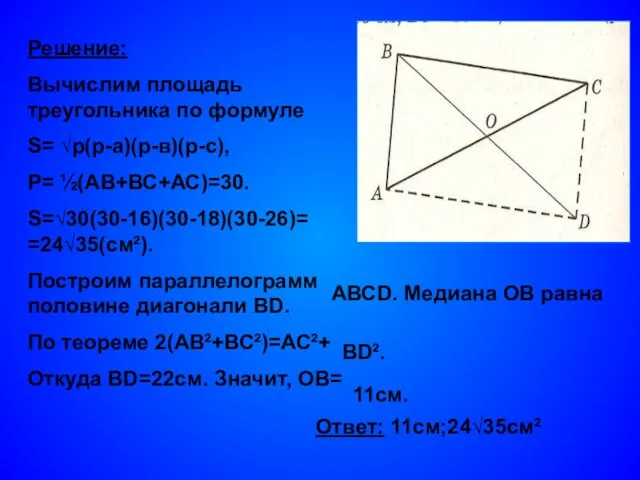
Задача №3.
Стороны треугольника равны 16см, 18см и 26см. Найти медиану, проведённую к большей стороне, и площадь треугольника.
Дано:
∆АВС,
АВ=16см,
ВС=18см,
АС=26см.
Найти: S треугольника АВС и медиану ОВ.

Решение:
Вычислим площадь треугольника по формуле
S= √р(р-а)(р-в)(р-с),
Р= ½(АВ+ВС+АС)=30.
S=√30(30-16)(30-18)(30-26)= =24√35(см²).
Построим параллелограмм половине диагонали ВD.
По теореме 2(АВ²+ВС²)=АС²+
Откуда ВD=22см. Значит, ОВ=
АВСD. Медиана ОВ равна
ВD².
11см.
Ответ: 11см;24√35см²

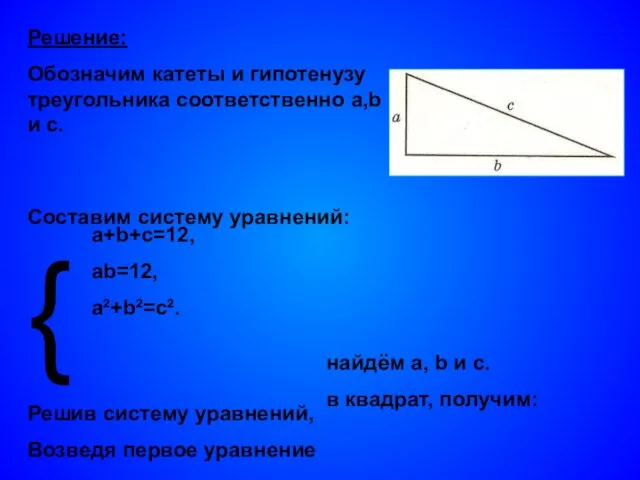
Задача №4.
Периметр прямоугольного треугольника равен 12см, а его площадь- 6см². Найти длины сторон треугольника.
Дано:
Прямоугольный треугольник,
S ∆ равна 6см²,
Р ∆ равен 12см.
Найти: Длины сторон ∆.

Решение:
Обозначим катеты и гипотенузу треугольника соответственно a,b и с.
Составим систему уравнений: {
Решив систему уравнений,
Возведя первое уравнение
a+b+c=12,
ab=12,
a²+b²=c².
найдём a, b и с.
в квадрат, получим:

a²+b²+c²+2(ab+ac+bc)=144.
a²+b²+c²+2[ab+c(a+b)]=144.
Но a²+b²=c², a+b=12-с →2 c²+2[12+с(12-с)]=144.
Отсюда с=5см. Таким образом, a+b=7.
a²+b²=25, а=3см, b=4см.
Ответ: 3см;4см;5см.

Задача №5.
Прямоугольная трапеция описана около окружности. Точка касания делит боковую сторону трапеции на отрезки длиной 2 и 8. Найдите периметр трапеции.
Дано:
АВСD-прямоугольная трапеция,
О(О;r)-вписанная окружность,
СК=2, КD=8.
Найти: Периметр трапеции.

Решение:
Центр О окружности, вписанной в трапецию АВСD с прямыми углами А и В, является точкой пересечения биссектрис углов трапеции. Т.к. в трапеции
<С+
Пусть окружность касается
точке К, тогда ОК┴CD.
В прямоугольном треугольнике
√CK· KD=√2· 8=4. Поскольку, СМ
точки М иТ- точки касания окру
пеции, получаем: р=2(2+8)+4· 4=
боковой стороны CD в
COD радиус ОК равен
=СК=2, TD=DK=8, где
жности и оснований тра-
36. Ответ:36.

И ещё…
Следует научить детей правильно заполнять бланки с ответами.