Содержание
- 2. Задание 2 Для какого из указанных значений Х истинно выражение: (Х>4) И НЕ ((Х>5) ИЛИ (Х
- 3. (Х>4) И НЕ ((Х>5) ИЛИ (Х По таблице истинности для операции логического умножения И: Значит высказывание
- 4. Рассмотрим когда (Х>5) ИЛИ (Х По таблице истинности для операции логического сложения ИЛИ: Значит высказывание (Х>5)
- 5. Варианты: 1)3 2)5 3)4 4)2 (Х>4) – истинно (Х>5) – ложно (Х Подставим вариант 1) 3
- 6. Пример 2. Для какого из указанных значений числа Х истинно выражение (X>2) & ¬(X>3)? 1) 1
- 7. Пример 3. Для какой из приведённых последовательностей цветных бусин истинно высказывание: (Последняя бусина зелёная) ИЛИ (Вторая
- 8. (Последняя бусина зелёная) ИЛИ (Вторая бусина красная) И (Четвёртая бусина зелёная) Решение: Для исходного высказывания (
- 10. Скачать презентацию







 Стандарты и спецификации в области информационной безопасности
Стандарты и спецификации в области информационной безопасности Получение разрешения на осуществление деятельности по проведению независимой идентификационной экспертизы товаров
Получение разрешения на осуществление деятельности по проведению независимой идентификационной экспертизы товаров С днём рождения, Мамочка
С днём рождения, Мамочка Себестоимость. Формула
Себестоимость. Формула Презентация на тему Все профессии важны (2 класс)
Презентация на тему Все профессии важны (2 класс) Коммерческое предложение по реализации имущества, прав требований. ООО НПП ЗППС БИНАКА
Коммерческое предложение по реализации имущества, прав требований. ООО НПП ЗППС БИНАКА Подходы к менеджменту: системный, ситуационный, процессный
Подходы к менеджменту: системный, ситуационный, процессный ProSpace (Казахстан)
ProSpace (Казахстан) Технология создания gif-анимации в Photoshop или ImageReady
Технология создания gif-анимации в Photoshop или ImageReady Эмпатическое слушание
Эмпатическое слушание vydacha_zadaniy (1) (1)
vydacha_zadaniy (1) (1) Отделка - это завершающая операция при изготовлении изделий
Отделка - это завершающая операция при изготовлении изделий Правотворческая деятельность на муниципальном уровне:
Правотворческая деятельность на муниципальном уровне: Пастернак Борис Леонидович ( 1890 - 1960 )
Пастернак Борис Леонидович ( 1890 - 1960 ) Презентация на тему СИЛА ТРЕНИЯ ПОКОЯ Силы в механике
Презентация на тему СИЛА ТРЕНИЯ ПОКОЯ Силы в механике  Dr.Web Enterprise Suite
Dr.Web Enterprise Suite Социальный контекст инновационного развития
Социальный контекст инновационного развития РМО учителей биологии и экологии
РМО учителей биологии и экологии Differences_between_British_and_American_versions_of_English_2 (2)
Differences_between_British_and_American_versions_of_English_2 (2) Диверсификация профессиональных навыков разработчикаДмитрий Васильев
Диверсификация профессиональных навыков разработчикаДмитрий Васильев Урок технологии
Урок технологии Практика построения системы управления техническим обслуживанием и ремонтами оборудования (ТОиР)(Использование программных инс
Практика построения системы управления техническим обслуживанием и ремонтами оборудования (ТОиР)(Использование программных инс Грузинский Технический Университет. Тбилиси
Грузинский Технический Университет. Тбилиси Перпендикулярность в пространстве (10 класс)
Перпендикулярность в пространстве (10 класс) Итоги Декады качества предоставления государственных услуг в сфере социальной поддержки и социального обслуживания населения
Итоги Декады качества предоставления государственных услуг в сфере социальной поддержки и социального обслуживания населения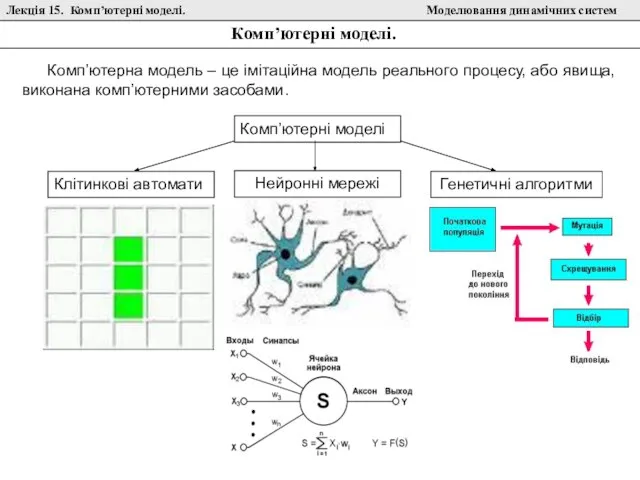 Клітинкові автомати
Клітинкові автомати Универсальная система учёта и паспортизации
Универсальная система учёта и паспортизации Мижоз хар доим хақ, энг ачинарлиси у бу хақида билади
Мижоз хар доим хақ, энг ачинарлиси у бу хақида билади