Содержание
- 2. выражает отношение длины окружности к своему диаметру. В этом качестве оно известно человеку с древнейших времен.
- 3. В залах нашего музея вы можете узнать: Об истории вычисления числа π Задача о квадратуре круга
- 4. Задача о квадратуре круга Абсолютно все знают, что такое "пи". Число π Число π
- 5. История вычисления числа π В Древнем Египте площадь круга диаметром d определяли как (d - d/9)2..
- 6. Загадочное число π История числа π, выражающего отношение длины окружности к её диаметру, началась в Египте.
- 7. Загадочное число π Спустя полтора столетия в Европе Ф.Виет нашёл число p только с 9 правильными
- 8. Пифагор Самосский Пифагор Самосский (др.-греч. Πυθαγόρας ὁ Σάμιος, лат. Pythagoras; 570—490 гг. до н. э.) —
- 9. Архимед Гордый Рим трубил победу Над твердыней Сиракуз; Но трудами Архимеда Много больше я горжусь. Надо
- 10. Архиме́д (Ἀρχιμήδης; 287 до н. э. — 212 до н. э.) — великий древнегреческий математик, физик,
- 11. Оценки числа π Архимед, дана в книге индийского мыслителя и астронома Арьябхаты в 5 веке н.
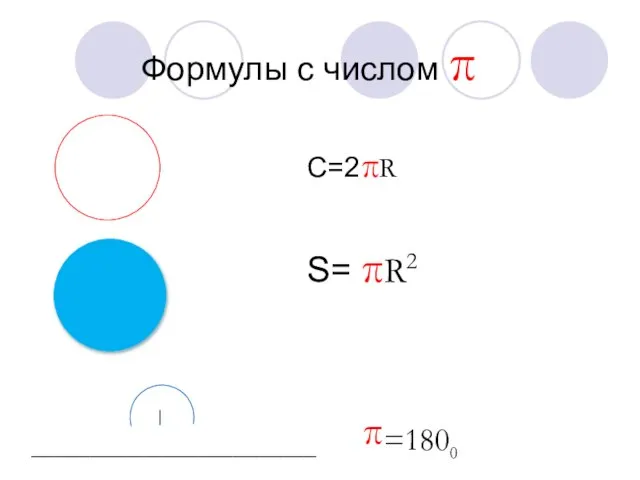
- 12. Формулы с числом π C=2πR S= πR2 ________________________ π=1800 A O B
- 13. Формулы с числом π Известно много формул с числом π: Франсуа Виет, 1593: Формула Валлиса: Ряд
- 14. Запомни знаки числа π Чтобы нам не ошибаться, Надо правильно прочесть: Три, четырнадцать, пятнадцать, Девяносто два
- 16. Скачать презентацию











 Необычный отель
Необычный отель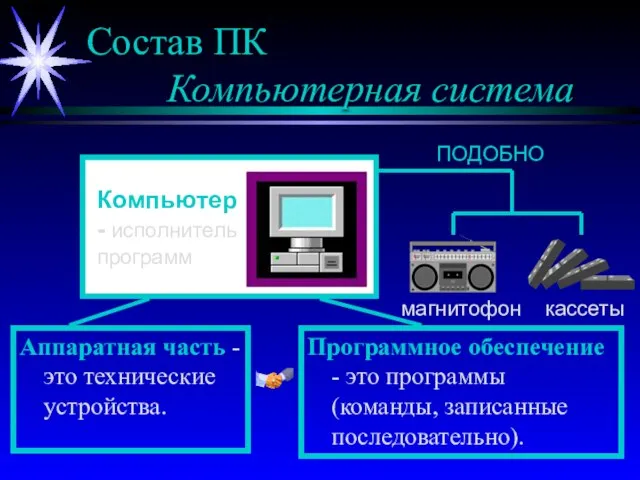 Состав ПК Компьютерная система
Состав ПК Компьютерная система 孔子学院在乌克兰和俄罗斯
孔子学院在乌克兰和俄罗斯 Places and Perspectives
Places and Perspectives Ресурси страховика
Ресурси страховика Метрическая система мер
Метрическая система мер Успешность адаптации ребенка при переходе со ступени начального образования – на основную
Успешность адаптации ребенка при переходе со ступени начального образования – на основную Istambek
Istambek Правила поведения итехники безопасности в кабинете информатики.
Правила поведения итехники безопасности в кабинете информатики. Город как среда обитания (5 класс)
Город как среда обитания (5 класс) Почему нужно чистить зубы?
Почему нужно чистить зубы? Автоматизированная система управления качеством вуза
Автоматизированная система управления качеством вуза Айдентика. Корпоративная идентификация
Айдентика. Корпоративная идентификация Повесть «Детство»
Повесть «Детство» Design Reboot
Design Reboot Клуб Алтын, доход посредством роста курса внутренней монеты
Клуб Алтын, доход посредством роста курса внутренней монеты Перспективы участия иностранных банков в развитии ритейлового бизнеса в российских регионах
Перспективы участия иностранных банков в развитии ритейлового бизнеса в российских регионах Работа с заданиями на анализ исторических версий и оценок.
Работа с заданиями на анализ исторических версий и оценок. Подготовка к ЕГЭ. (окончания глаголов и суффиксов причастий)
Подготовка к ЕГЭ. (окончания глаголов и суффиксов причастий) Проблемы начала правоприменения в сфере борьбы с картелями – опыт Бразилии
Проблемы начала правоприменения в сфере борьбы с картелями – опыт Бразилии Сложноподчиненные предложения с определительными придаточными
Сложноподчиненные предложения с определительными придаточными Фразеологическое ядро старославянского языка
Фразеологическое ядро старославянского языка План развития ЮФО 2020
План развития ЮФО 2020 Конструктивизм
Конструктивизм Мартиничка
Мартиничка Электронное портфолио ученика
Электронное портфолио ученика Магистерская программа 031100.68.20 Сопоставительное изучение культур и межкультурная коммуникация
Магистерская программа 031100.68.20 Сопоставительное изучение культур и межкультурная коммуникация Презентация на тему Украшение пасхального яйца
Презентация на тему Украшение пасхального яйца