Содержание
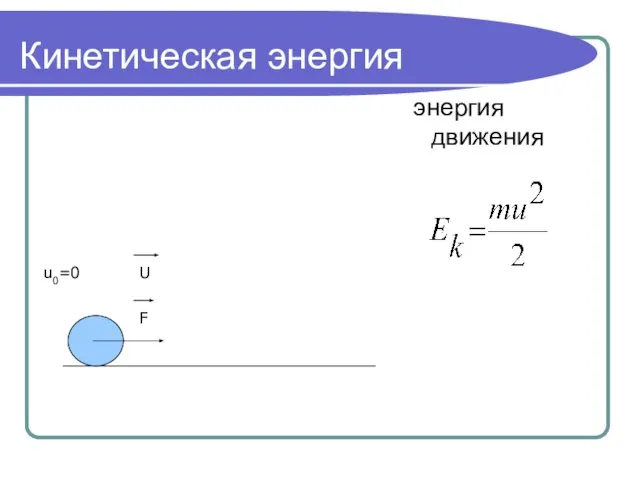
- 2. Кинетическая энергия энергия движения u0=0 F U
- 3. Герман Гельмгольц Впервые математически обосновал закон сохранения энергии, показав его всеобщий характер.Разработал термодинамическую теорию химических процессов,
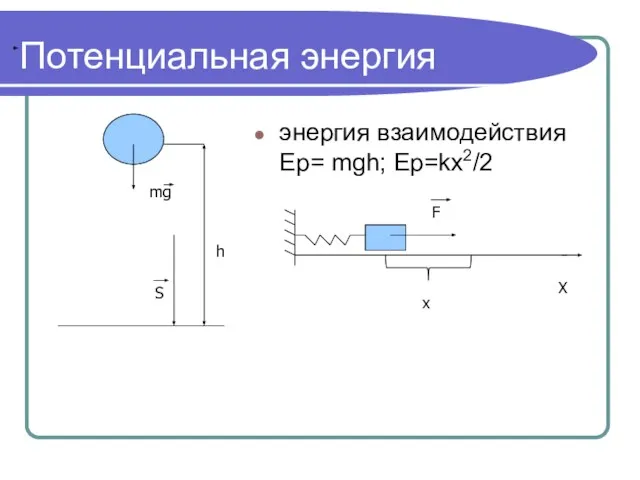
- 4. Потенциальная энергия энергия взаимодействия Ep= mgh; Ep=kx2/2 h mg S x F X
- 5. Полная механическая энергия Е=Ек+Еp
- 6. Закон сохранения энергии 1847г «Если тела действуют друг на друга с силами, не зависимыми от времени
- 7. ∆Е= ∆ Ек + ∆ Еp, но А= ∆Ек, а ∆Еp=∆t Еp-А пот ∆Е=А+∆t Еp-А пот
- 8. Теорема об изменении механической энергии Изменение механической энергии системы равно сумме работы сил трения и изменения
- 9. Эмми Нётер Труды Нетер по алгебре способствовали созданию нового направления, названного общей алгеброй. Сформулировала фундаментальную теорему
- 10. Теорема Нётер Каждому свойству симметрии пространства и времени соответствует свой закон сохранения энергии
- 11. Закон сохранения энергии При любых процессах, происходящих в замкнутой, потенциальной системе, её полная механическая энергия остается
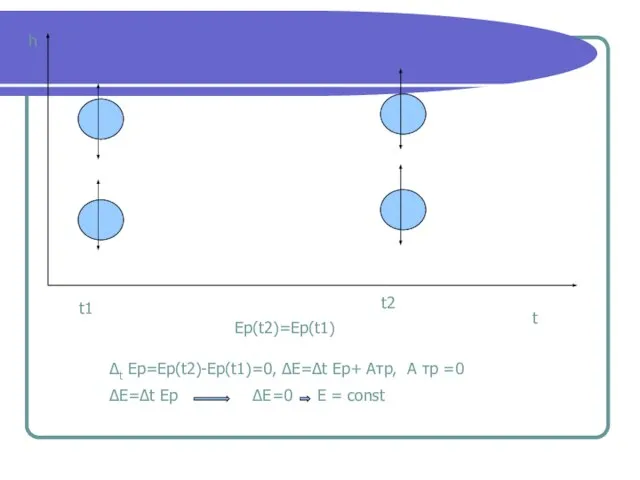
- 12. h t t1 t2 Ep(t2)=Ep(t1) ∆t Еp=Ep(t2)-Ep(t1)=0, ∆Е=∆t Еp+ Атр, А тр =0 ∆Е=∆t Еp ∆Е=0
- 13. Закон сохранения энергии При любых процессах, происходящих в консервативных системах, её полная механическая энергия остается постоянной
- 14. Ek + Ep =const В процессе движения системы всякое увеличение кинетической энергии системы должно сопровождаться соответствующим
- 15. – давление горизонтально текущей жидкости (или газа) больше в тех местах потока, в которых скорость ее
- 16. Даниил Бернулли (1700-1782) Закон Бернулли справедлив для идеальной жидкости (т. е. жидкости, в которой можно пренебречь
- 17. Этим явлением объяс-няется и возникновение подъемной силы, дейст-вующей на крылья самолета.
- 18. Николай Егорович Жуковский(1847-1921) Теория возник-новения подъемной силы крыла само-лета была разра-ботана русским ученым Николаем Егоровичем Жуковским.
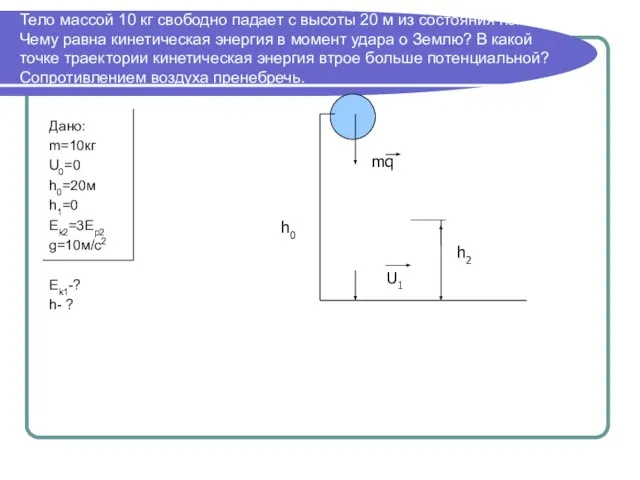
- 19. Тело массой 10 кг свободно падает с высоты 20 м из состояния покоя. Чему равна кинетическая
- 20. Еp0+Ek0=Ep1+Ek1 U0=0 и h1=0 Ek1=mgh0, Ek1= 10*10*20=2000 Дж Запишем закон сохранения энергии для точки траектории, где
- 22. Скачать презентацию















 Ты, человек, любя природу,Хоть иногда её жалей:В увеселительных походахНе растопчи её полей.В вокзальной сутолоке векаТы оценит
Ты, человек, любя природу,Хоть иногда её жалей:В увеселительных походахНе растопчи её полей.В вокзальной сутолоке векаТы оценит NXP semiconductors, Москва. Краткий обзор
NXP semiconductors, Москва. Краткий обзор Однофазный TIG-инвертор
Однофазный TIG-инвертор Індекси цін у будівництві
Індекси цін у будівництві Банки и банковская система РФ. Тест
Банки и банковская система РФ. Тест Прикладной Тайм-менеджмент для программистов
Прикладной Тайм-менеджмент для программистов ГПОУ Горловский автотранспортный техникум. ГОУВПО Донецкий национальный технический университет
ГПОУ Горловский автотранспортный техникум. ГОУВПО Донецкий национальный технический университет Кабинет министров
Кабинет министров Республиканский научно-исследовательский институт интеллектуальной собственности ул. Б.Якиманка, д. 38, г. Москва, 119049 тел./факс: +
Республиканский научно-исследовательский институт интеллектуальной собственности ул. Б.Якиманка, д. 38, г. Москва, 119049 тел./факс: + Доброволец на ЧС. Особенности психологической устойчивости личного состава. Способы подготовки
Доброволец на ЧС. Особенности психологической устойчивости личного состава. Способы подготовки Сессия Госконтроль 2.0: образ будущего
Сессия Госконтроль 2.0: образ будущего Презентация Microsoft PowerPoint
Презентация Microsoft PowerPoint Перпендикуляр и наклонные
Перпендикуляр и наклонные Однородные члены предложения
Однородные члены предложения Предмет, метод, источники и принципы Трудового права
Предмет, метод, источники и принципы Трудового права Поэты Ставрополья о родном крае и о природе родного края
Поэты Ставрополья о родном крае и о природе родного края Педагогический совет «Поиск путей совершенствования образовательной среды школы при введении федерального государственного обр
Педагогический совет «Поиск путей совершенствования образовательной среды школы при введении федерального государственного обр Обзор на персонажа
Обзор на персонажа ВКР: Действительный цикл машины МВВ6 - 1 -2
ВКР: Действительный цикл машины МВВ6 - 1 -2 15 февраля 1861 года родился швейцарский физик-метролог Шарль Эдуард Гильом (Гийом).
15 февраля 1861 года родился швейцарский физик-метролог Шарль Эдуард Гильом (Гийом). Правила наложения жгутов повязок и шин
Правила наложения жгутов повязок и шин Вальдорфская система образования
Вальдорфская система образования Social Ecology Sustainable Development
Social Ecology Sustainable Development  Ваш профессиональный маршрут
Ваш профессиональный маршрут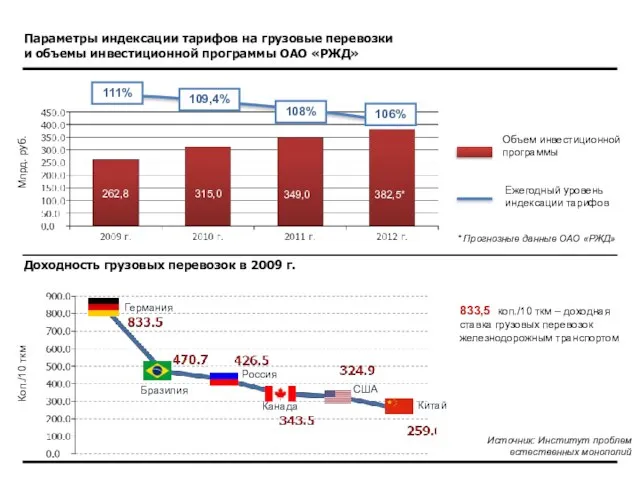 Параметры индексации тарифов на грузовые перевозки и объемы инвестиционной программы ОАО «РЖД»
Параметры индексации тарифов на грузовые перевозки и объемы инвестиционной программы ОАО «РЖД» Концепция воспитательной системы
Концепция воспитательной системы Технология создания и редактирования изображений в векторном редакторе
Технология создания и редактирования изображений в векторном редакторе Презентация на тему Использования краеведческого материала в образовательном процессе
Презентация на тему Использования краеведческого материала в образовательном процессе