Слайд 2Работу представляет Викторова Виктория,
ученица 5 класса
Курлекской СОШ
Руководитель Логунова Л.В. – учитель математики

Слайд 3Наглядное пособие
по математике
для младших школьников
Замечательная фигура - квадрат!
О квадрате
Геометрия квадрата
Квадрат

– «лучше» других фигур
Волшебный квадрат
Слайд 4О квадрате
Присмотритесь-ка к квадрату:
Он здоровый, тароватый,
Он надежнее как друг,
Чем уж слишком круглый
круг.
В нем четыре стороны
И все стороны равны.
Честен каждою чертой,
Каждый угол в нем прямой.
Тем еще квадрат отличен,
Что вполне он симметричен,
Треугольников всех рать
Вам того не может дать.
Е. Паин
Слайд 5Геометрия квадрата
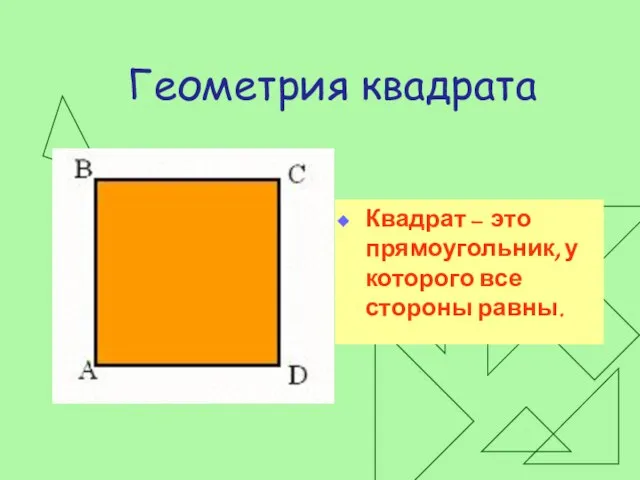
Квадрат – это прямоугольник, у которого все стороны равны.
Слайд 6Что вы знаете о квадрате?
У квадрата:
все углы прямые;
все стороны равны;
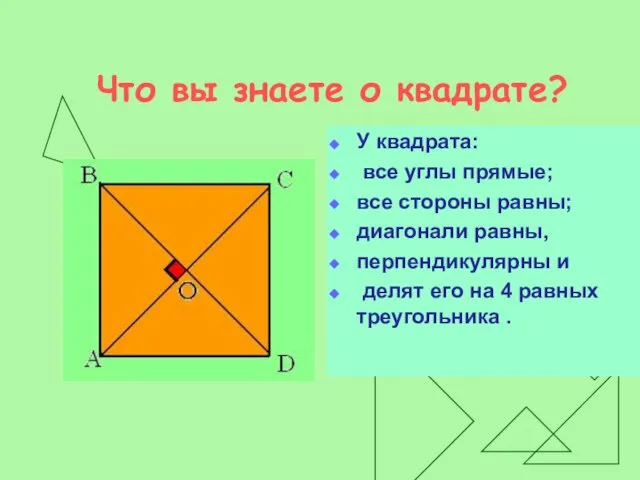
диагонали равны,
перпендикулярны и
делят его на 4 равных треугольника .
Слайд 7Квадрат симметричная фигура?
Одна ось симметрии квадрата проходит через противоположные вершины квадрата.
Есть ли
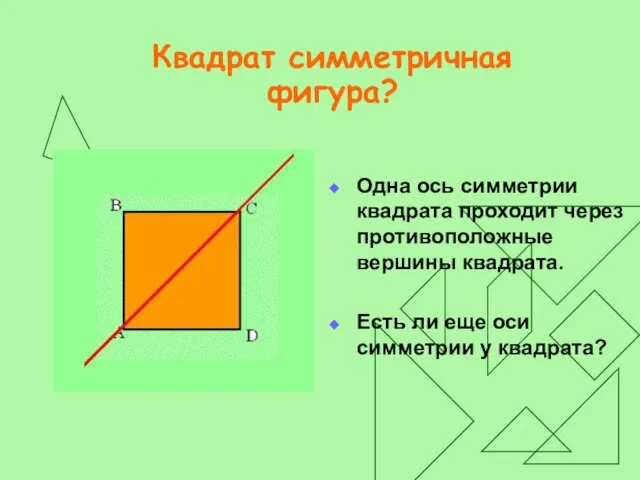
еще оси симметрии у квадрата?
Слайд 8Объясните, в чем состоит симметрия квадрата на рисунках?
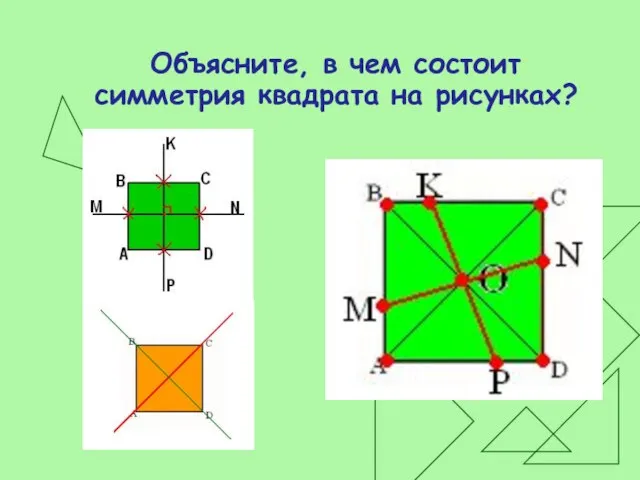
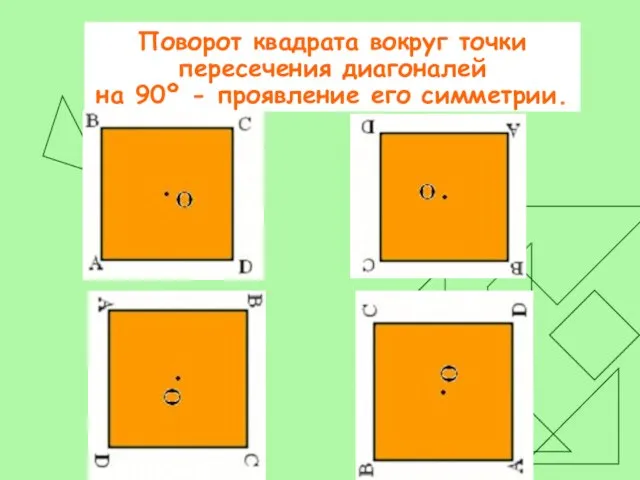
Слайд 9Поворот квадрата вокруг точки пересечения диагоналей
на 90º - проявление его симметрии.
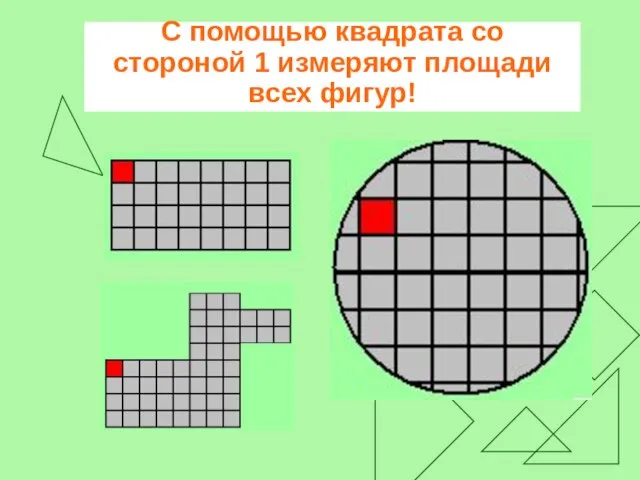
Слайд 10С помощью квадрата со стороной 1 измеряют площади всех фигур!
Слайд 11Квадрат «лучше» других фигур?
Рассмотрим уже доказанные факты(примеры)
Слайд 12Пример 1.
Изготовление открытой коробочки из квадратного листа
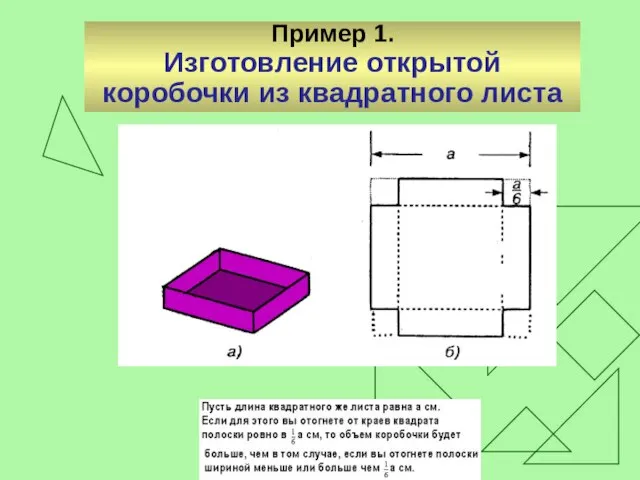
Слайд 13Пример 2.
«Какой из прямоугольников данной площади имеет наименьший периметр»?
Квадрат
Слайд 14Пример 3.
Какой прямоугольник имеет наибольшую площадь с заданным периметром?
Квадрат
Слайд 15Пример 4 .
«Задание директора!»
Расширить площадку так, чтобы:
1) Сохранить прямоугольную форму площадки, но
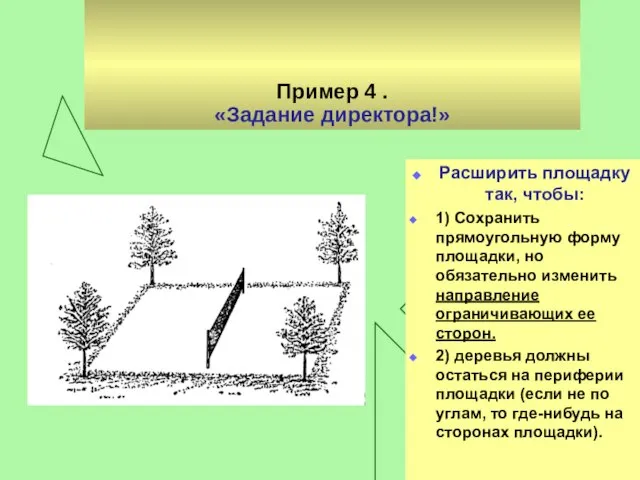
обязательно изменить направление ограничивающих ее сторон.
2) деревья должны остаться на периферии площадки (если не по углам, то где-нибудь на сторонах площадки).
Слайд 16Пример 4 .
Ученики думали, чертили, выясняли
Расчеты показали, что площади описанных прямоугольников неодинаковы,
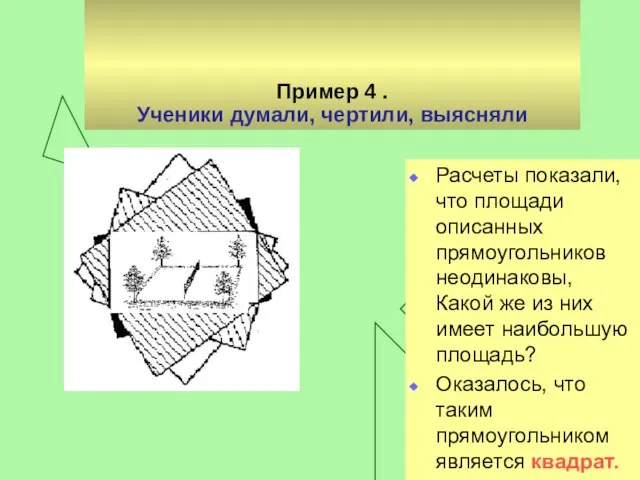
Какой же из них имеет наибольшую площадь?
Оказалось, что таким прямоугольником является квадрат.
Слайд 17Пример 5 .
Квадрат в квадрате
Соедините последовательно середины сторон квадрата АВСО отрезками и
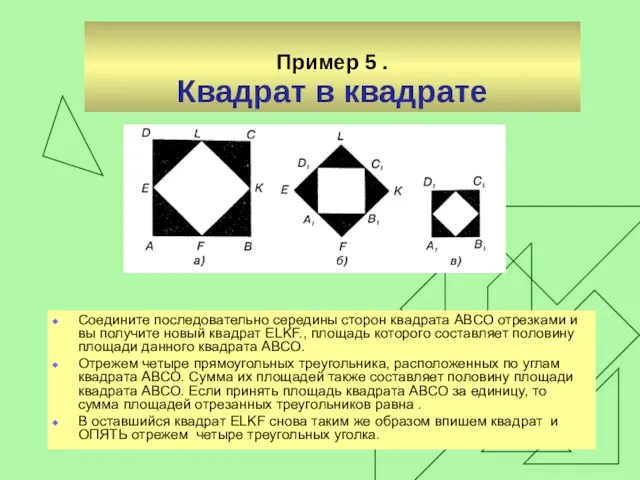
вы получите новый квадрат ЕLKF., площадь которого составляет половину площади данного квадрата АВСО.
Отрежем четыре прямоугольных треугольника, расположенных по углам квадрата АВСО. Сумма их площадей также составляет половину площади квадрата АВСО. Если принять площадь квадрата АВСО за единицу, то сумма площадей отрезанных треугольников равна .
В оставшийся квадрат ЕLKF снова таким же образом впишем квадрат и ОПЯТЬ отрежем четыре треугольных уголка.
Слайд 20Пример 6 .
Правило квадрата в шахматах
Как определить, пройдет ли белая пешка в
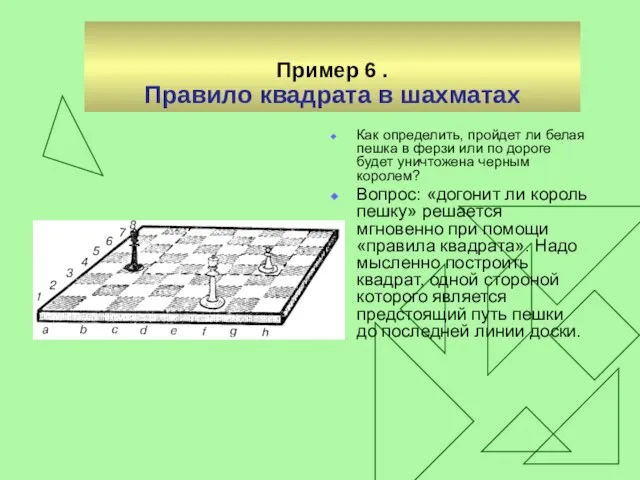
ферзи или по дороге будет уничтожена черным королем?
Вопрос: «догонит ли король пешку» решается мгновенно при помощи «правила квадрата». Надо мысленно построить квадрат, одной стороной которого является предстоящий путь пешки до последней линии доски.
Слайд 21Пример 6 .
Правило квадрата в шахматах
Тогда, если король противника войдет в этот

квадрат (с любой его стороны) раньше, чем пешка покинет вершину угла квадрата, то король догонит пешку, если нет, то пешка проходит в ферзи, при ходе черных король попадет в очерченный квадрат и, следовательно, задержит пешку белых; при ходе белых король черных не успевает вступить в очерченный квадрат, и белые выигрывают. Вот и все правило квадрата
Слайд 22Пример 6 .
Правило квадрата в шахматах
Если пешка находится в начальном положении как
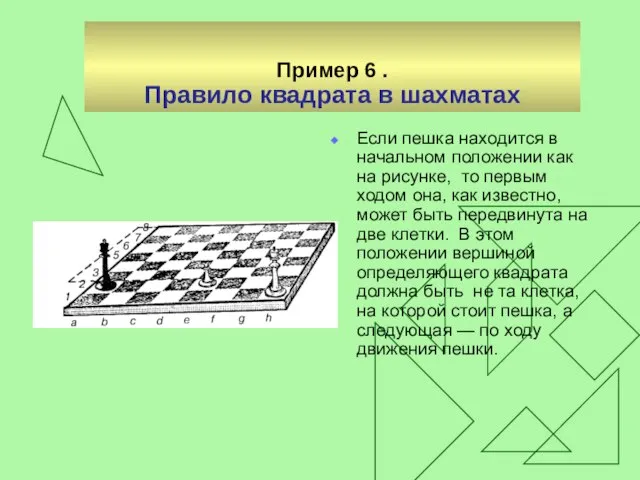
на рисунке, то первым ходом она, как известно, может быть передвинута на две клетки. В этом положении вершиной определяющего квадрата должна быть не та клетка, на которой стоит пешка, а следующая — по ходу движения пешки.
Слайд 23Волшебный квадрат
Волшебные квадраты придуманы впервые китайцами, так как самое раннее упоминание о
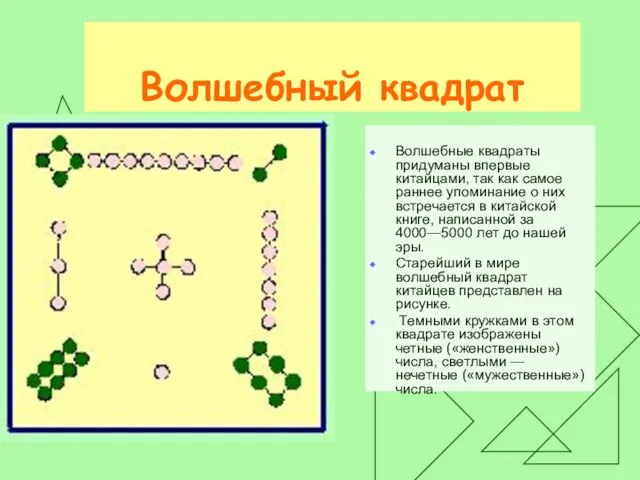
них встречается в китайской книге, написанной за 4000—5000 лет до нашей эры.
Старейший в мире волшебный квадрат китайцев представлен на рисунке.
Темными кружками в этом квадрате изображены четные («женственные») числа, светлыми — нечетные («мужественные») числа.
Слайд 24 В обычной записи он не так красив. Смотрите.
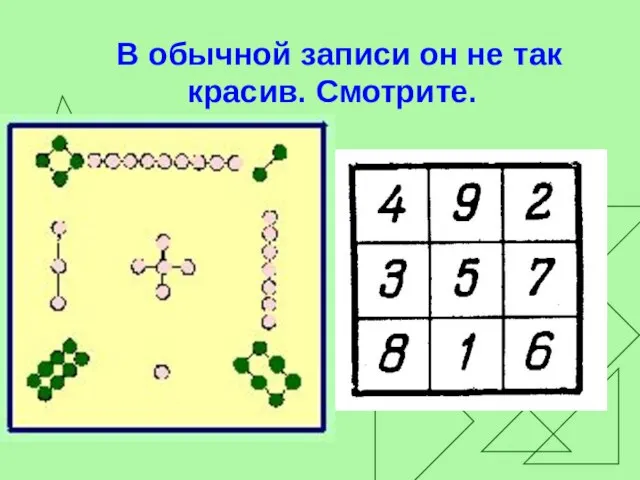
Слайд 25Это - наименьший волшебный квадрат
Составление магических квадратов, или, волшебных квадратов – старинный
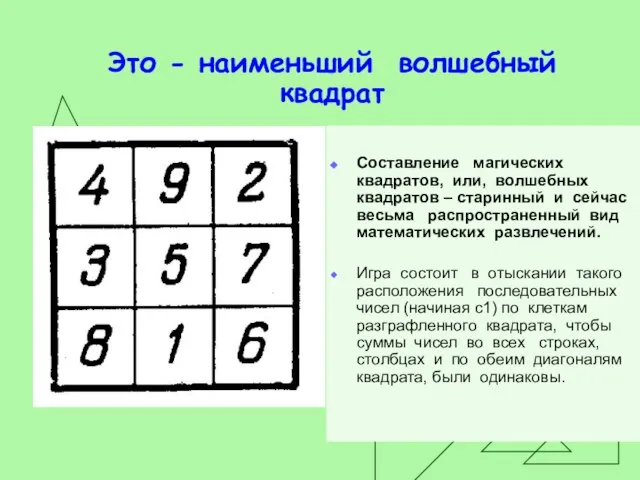
и сейчас весьма распространенный вид математических развлечений.
Игра состоит в отыскании такого расположения последовательных чисел (начиная с1) по клеткам разграфленного квадрата, чтобы суммы чисел во всех строках, столбцах и по обеим диагоналям квадрата, были одинаковы.
Слайд 26Это магический квадрат 4-ого порядка
Каждое число волшебного квадрата участвует в двух суммах,
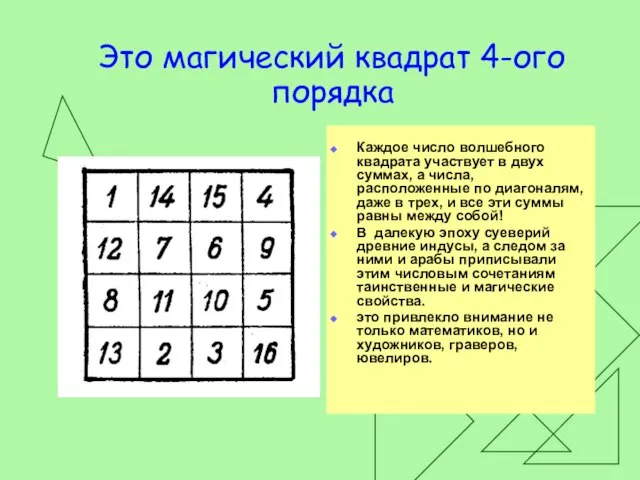
а числа, расположенные по диагоналям, даже в трех, и все эти суммы равны между собой!
В далекую эпоху суеверий древние индусы, а следом за ними и арабы приписывали этим числовым сочетаниям таинственные и магические свойства.
это привлекло внимание не только математиков, но и художников, граверов, ювелиров.
Слайд 27Пятнашки
Игра в «15» заключается в том, что, предварительно расположив в коробке все
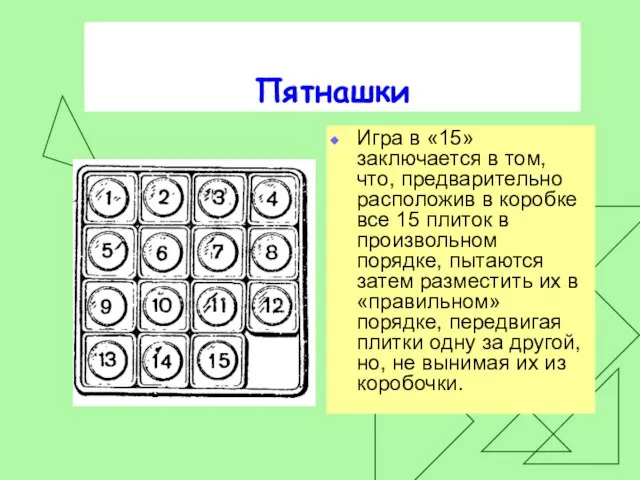
15 плиток в произвольном порядке, пытаются затем разместить их в «правильном» порядке, передвигая плитки одну за другой, но, не вынимая их из коробочки.
Слайд 28Самуэль Лойд – изобретатель головоломки («Пятнашки»)
Головоломка появилась в 70-ых годах 19 века
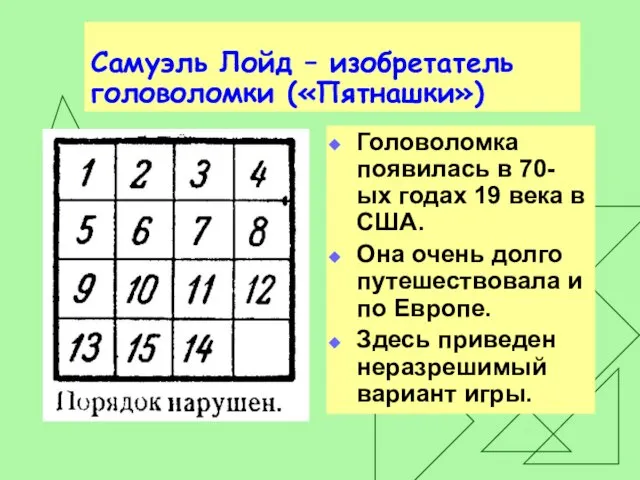
в США.
Она очень долго путешествовала и по Европе.
Здесь приведен неразрешимый вариант игры.
Слайд 29О квадрате
Квадрат – настолько неисчерпаемая фигура, применяемая во многих сферах, что по
каждому разделу в содержании реферата можно провести серьезную исследовательскую работу.




























 Мероприятия по информированию, вовлечению, анкетированию, отбору и обучению
Мероприятия по информированию, вовлечению, анкетированию, отбору и обучению Питер. 03.04.2017
Питер. 03.04.2017 Лиса в русских народных сказках
Лиса в русских народных сказках Фирмы в экономике
Фирмы в экономике How much do you know about English Christmas?
How much do you know about English Christmas? Функциональные возможности дыхательной системы
Функциональные возможности дыхательной системы Оценочная деятельность учителя
Оценочная деятельность учителя Informace pro studenty
Informace pro studenty Видеоэкология
Видеоэкология Тема: «Живая и неживая природа»
Тема: «Живая и неживая природа» Тепловые явления
Тепловые явления Этапы речевого развития
Этапы речевого развития Писатели и поэты Кубани
Писатели и поэты Кубани Презентацию подготовила библиотекарь МБОУ СОШ №5 Танина С.П
Презентацию подготовила библиотекарь МБОУ СОШ №5 Танина С.П Презентация на тему Family Businesses (Семейный бизнес)
Презентация на тему Family Businesses (Семейный бизнес) Описание объекта
Описание объекта Порядок вступления в силу нормативных правовых актов
Порядок вступления в силу нормативных правовых актов «Женщины Архангельской области: вчера, сегодня, завтра» Н.А. Макарова, председатель РОО «Совет женщин Архангельской области» г
«Женщины Архангельской области: вчера, сегодня, завтра» Н.А. Макарова, председатель РОО «Совет женщин Архангельской области» г Презентация на тему Нефтяная промышленность США
Презентация на тему Нефтяная промышленность США Спасообыденная церковь – прошлое и настоящее
Спасообыденная церковь – прошлое и настоящее Три состояния воды
Три состояния воды Технічне обслуговування верстата HAAS EC-400, який використовується для механічної обробки деталі Люлька PVS71-09.001
Технічне обслуговування верстата HAAS EC-400, який використовується для механічної обробки деталі Люлька PVS71-09.001 Финансовый механизм коммерческого предприятия
Финансовый механизм коммерческого предприятия Волшебное преображение кляксы
Волшебное преображение кляксы Презентация на тему Харганатская средняя общеобразовательная школа
Презентация на тему Харганатская средняя общеобразовательная школа  Русская культура в произведениях русских классиков
Русская культура в произведениях русских классиков Основы государства и права. Законность и порядок
Основы государства и права. Законность и порядок Народные обереговые куклы Козьма и Демьян
Народные обереговые куклы Козьма и Демьян